Geometria Espacial - Escola Professor Jonathas Pontes Athias

Fundação
Vale do Trombetas
Escola Professor Jonathas Pontes Athias
Disciplina: Matemática
Série: 3ª
Turma: 321
Etapa: 1ª
Data: 19.02.2010
Nome do Aluno:
N°
Professor: Reginaldo Lima
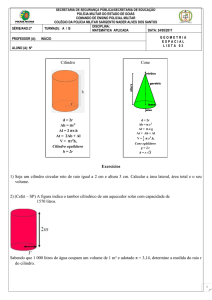
Geometria Espacial
CILINDRO - Classificação e Elementos.
CONE - Classificação e Elementos.
Cone Oblíquo: Quando o eixo é oblíquo a base.
Cone Reto: Quando o eixo é perpendicular à base.
Obs: Se a altura do cilindro for igual ao
diâmetro da base, ou seja, h = 2R, então a
secção meridiana é um quadrado e o
cilindro é chamado Cilindro Eqüilátero.
Áreas e Volume
Obs:
Se
a
secção
meridiana de um cone for
um triângulo eqüilátero,
ou seja, g = 2R, então, o
cone
é
dito
Cone
Eqüilátero.
Áreas e Volume
TRONCO DE CONE
ÁREA DA SUPERFÍCIE ESFÉRICA E
VOLUME DA ESFERA
ÁREA
4 R 2
VOLUME
4 3
R
3
SECÇÃO DE UMA ESFERA
OO é a distância do plano  ao centro da esfera.
Qualquer plano  que secciona uma esfera de raio R
determina como secção plana um círculo de raio R.
OO  d , temos:
2
R 2  d 2  R  
Sendo
TRONCO PLANIFICADO
Quando o plano que secciona a esfera contiver um
diâmetro, teremos d  0 . Nesse caso, o círculo
determinado terá raio R e será denominado círculo
máximo.
FUSO ESFÉRICO
É a parte da superfície esférica compreendida entre dois
semicírculos máximos com o mesmo diâmetro.
ÁREA DO FUSO ESFÉRICO:
 EM GRAUS:
AF 
 R 2
90 
SUPERFÍCIE ESFÉRICA
Chama-se superfície esférica de centro O e raio R o
conjunto dos pontos do espaço cujas distâncias a O
são iguais a R, ou seja, é o conjunto de pontos P do
espaço eqüidistante de um ponto fixo O, chamado de
centro da superfície esférica.
ESFERA
É o conjunto de todos os pontos do espaço cujas
distâncias ao ponto O são menores ou iguais a R, ou
seja, é a região do espaço limitada por uma superfície
esférica. Seu centro e seu raio são os da superfície
esférica correspondente.
 EM RADIANO:
AF  2R 2
CUNHA ESFÉRICA
É o sólido limitado por dois semicírculos e pelas superfície
do fuso.
VOLUME DA CUNHA ESFÉRICA:
 EM GRAUS:
VCunha 
 R 3
270 
 EM RADIANO:
2 R 3
VCunha 
3
TESTES DE VESTIBULARES
1) (Mack – SP) – Uma esfera de diâmetro 6 cm está
inscrita em um cone circular reto de altura 8 cm.
Então a área da base do cone vale:
a)
54 cm 2
c)
44 cm 2
b)
48 cm 2
d)
40 cm 2
e)
36 cm 2
5) (Mack – SP) – Uma xícara de chá
tem a forma de um tronco de cone
reto, conforme a figura. Supondo
  3 , o volume máximo de líquido
que ela pode conter é:
168 cm 3
3
b) 172 cm
166 cm 3
3
d) 176 cm
a)
2) (FGV – SP) – Um cálice com a
3
forma de um cone contém V cm
de uma bebida. Uma cereja de
forma esférica com diâmetro de
2 cm é colocada dentro do cálice.
Supondo-se que a cereja repousa
apoiada nas laterais do cálice e o
líquido recobre exatamente a
cereja a altura de 4 cm a partir
do vértice do cone, determine o valor de V.
3) (UFSCar – SP) – A figura representa um galheteiro
para a colocação de azeite e vinagre em
compartimento diferentes, sendo um cone no
interior de um cilindro.
c)
e)
164 cm 3
6) (UEL – PR) – Seja g a geratriz de um cone circular reto
inscrito num cilindro circular reto de mesma área lateral,
base e altura. O volume desse cone é:
a)
b)
 g3
c)
24
 g3
d)
8
 g3
e)
12
3 g 3
2
2 g 3
3
7) (UM – SP) – Num copo, que tem a forma de um cilindro
reto de altura 10 cm e raio da base 3 cm, são
introduzidos 2 cubos de gelo, cada um com 2 cm de
aresta. Supondo   3 , o volume máximo de líquido que
se pode colocar no copo é:
a) 158 ml
b) 230 ml
c) 300 ml
d) 254 ml
e) 276 ml
8) (UA – AM) – Um copo de vidro com formato de um
cilindro circular reto, cujo diâmetro interno mede 4 cm,
está cheio de um líquido até a borda. Inclinando esse
copo, despeja-se o líquido nele contido até que atinja a
marca que dista da borda
16

cm . O volume do líquido
despejado é:
Considerando h como altura máxima de líquido
que o galheteiro comporta e a razão entre a
capacidade total de azeite e vinagre igual a 5, o
valor de h é:
a) 7 cm
b) 8 cm
c) 10 cm
d) 12 cm
4) (UFSM – RS) – Bolas de tênis são
vendidas,
normalmente,
em
embalagens cilíndricas contendo 3
unidades. Supondo-se que as bolas
têm raio a em centímetros, e
tangenciam as paredes internas da
embalagem, o espaço interno dessa
embalagem que não é ocupado pelas
bolas é:
a)
b)
2 a 3
4 3
a
3
c)
d)
a
3
a)
36 cm 3
b)
16 cm 3
c)
64 cm 3
d)
32 cm 3
e)
80 cm 3
e) 15 cm
GABARITO DOS TESTES
1
3
e)
2 3
a
3
a3
Reflita!
“O que importa,
Não é a vitória, mas o esforço.
Não é o talento, mas a vontade.
Não é quem você é, mas quem você quer
ser.”
2
e
4
3
5
a
6
b
3
c
7
d
4
a
8
d