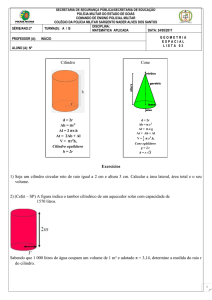
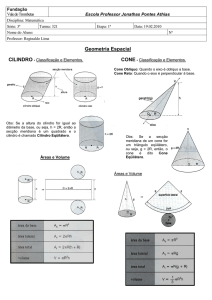
.::. Um cone e uma esfera.
.::. Uma questão que pode ser muito interessante é quando uma esfera de raio R "cai" dentro
de um cone reto de altura h e raio da base r. A situação é ilustrada abaixo:
.::. Podemos observar que a esfera está a uma distância d do vértice do cone, sendo esta a
menor distância. Os pontos M e N são pontos de tangência, e g é a geratriz do cone.
Queremos determinar a menor distância que a esfera está do vértice do cone. Para isso,
traçamos um segmento de reta do centro O da esfera a cada um dos pontos de tângencia da
geratriz do cone com a esfera.
.::. Os ângulos OMA e ONA são retos, pois os pontos M e N sãp pontos de tangência. Os
ângulos MÂO e NÂO também pertencem aos triângulos retângulos PÂC e PÂB,
respectivamente. Temos, portanto, um caso de semelhança de triângulos Ângulo - Ângulo.
Publicado por Rodrigo R. Gonçalez – 02/11/2007
.::. O teorema da semelhança de triângulos nos diz que se dois ângulos de um triângulo
qualquer são congruentes a dois ângulos de um outro triângulo qualquer, então esses
triângulos são semelhantes e seus lados homólogos são proporcionais.
.::. Logo, temos: ∆PÂC ∼ ∆MÂO
.::. Então:
R+d R
=
g
r
Rr + dr = Rg
dr = Rg − Rr
dr = R( g − r )
R( g − r )
d=
r
.::. Podemos ainda fazer:
g ² = h² + r ²
g = h² + r ²
Logo,
d=R
( h² + r ² − r )
r
.::. Vemos que quanto maior o raio da esfera R ou quanto menor o raio r da base do cone,
maior é d. E também que quanto menor o raio da esfera R ou maior o raio r da base do cone,
menor é d.
Publicado por Rodrigo R. Gonçalez – 02/11/2007
.::. Observamos de importante que a menor distância do vértice do cone a superfície da
esfera depende do raio da esfera, do raio da base do cone e da altura do cone. O ponto
mais distante da esfera ao vértice do cone é dado por:
( h² + r ² − r )
r
( h² + r ² − r )
D = R 2 +
r
2r + h ² + r ² − r
D = R
r
( h² + r ² + r )
D = R
r
D = 2R + R
.::. Como queríamos demonstrar.
Publicado por Rodrigo R. Gonçalez – 02/11/2007