aprovar_ano04_modulo03_apostila22_completa (1321771)

• Matemática – Prismas e
pirâmides
pg. 02
• Matemática – Sólidos circulares
pg. 04
• Física – Eletrodinâmica I
• Física – Eletrodinâmica II
pg. 06
pg. 08
• Português – Parnasianismo
pg. 10
Trichechus inungui, o peixe boi
4,5 metros e vive entre –as da Amazônia, pode chegar aos 750kg e
bacias dos rios Amazonas e
Orinoco
ir
Brasile
a
i
m
e
d
Aca
as de 1901
g
e
l
o
c
eus
de
he) e s o, em foto
l
a
t
e
d
ir
o
ilac (n Rio de Jane
B
o
v
a
Ol tras, no
de Le
a
Sábado é dia
de Simuladão
Matemática
A(lateral) = n . A(face lateral)
– Uma forma alternativa para obter a área lateral
de um prisma reto tendo como base um
polígono regular de n lados é tomar P como o
perímetro desse polígono e h como a altura
do prisma.
A(lateral) = P.h
Professor CLÍCIO
Prismas e pirâmides
Aplicação
Prisma é um sólido geométrico delimitado por
faces planas, no qual as bases se situam em
planos paralelos.
Quanto à inclinação das arestas laterais, os
prismas podem ser retos ou oblíquos.
3
Um prisma reto, de volume igual a 36cm , tem
como base um triângulo retângulo de hipotenusa
igual a
cm e como catetos números inteiros
consecutivos, medidos em centímetros. Calcule,
em centímetros, a altura H deste prisma.
Solução:
Catetos do triângulo: x, x + 1
2
2
x + (x + 1) = 13 , então x = 2. Logo os catetos
são 2 e 3;
Vp = Ab . H, então 36=3H, então H=12cm
Cubo
Um paralelepípedo retângulo com todas as
arestas congruentes ( a= b = c) recebe o nome
de cubo. Dessa forma, as seis faces são
quadrados.
No próximo sábado, dia 8, às 17h, a UEA
realiza o primeiro SIMULADÃO de 2007,
com as disciplinas ministradas nos dois
primeiros módulos: Português, Geografia
e História. É uma oportunidade de você
avaliar o aprendizado adquirido até
agora e testar seus conhecimentos.
Participe. A entrada é gratuita.
Quanto à base, os prismas mais comuns estão
mostrados na tabela:
Além disso, é uma chance para você tirar
suas dúvidas com os próprios professores
que ministraram as disciplinas. Ao término
da prova, todas as questões serão
analisadas por eles, e as respostas
exibidas nos telões.
Seções de um prisma
Na página 11, você vai encontrar uma
a) Seção transversal – a
região poligonal obtida pela
interseção do prisma com um
plano paralelo às bases,
sendo que esta região
poligonal é congruente a cada
uma das bases.
b) Seção reta (seção normal)
– É uma seção determinada por um plano
perpendicular às arestas laterais.
ficha que deve ser preenchida e entregue
no dia do teste. O SIMULADÃO terá 30
questões, sendo 10 de Português e
Literatura, 10 de História e 10 de
Geografia.
O gabarito oficial será publicado na
Apostila número 23, que circula no
próximo domingo, dia 16, encartada nos
jornais Diário do Amazonas, O Estado do
Amazonas, Jornal do Commercio e
Amazonas em Tempo, podendo também
ser acessado pelos sites e
www.linguativa.com.br, onde você vai
encontrar, também, números anteriores
de apostilas e todas as informações
sobre o Aprovar.
Na contracapa desta apostila, você vai
encontrar uma relação com os endereços
das 13 escolas da capital onde será
aplicado o SIMULADÃO. No interior, a
prova será nos Núcleos e Centros da
UEA e nas escolas que recebem
regularmente as transmissões das aulas
Diagonais da base e do cubo
Considere a figura a seguir:
dc=diagonal do cubo
Princípio de Cavalieri – Consideremos um
plano P sobre o qual estão apoiados dois
sólidos com a mesma altura. Se todo plano
paralelo ao plano dado interceptar os sólidos
com seções de áreas iguais, então os volumes
dos sólidos também serão iguais.
Prisma regular
É um prisma reto cujas bases são regiões poligonais regulares.
Exemplos: Um prisma triangular regular é um
1. prisma reto cuja base é um triângulo
equilátero.
2. Um prisma quadrangular regular é um prisma
reto cuja base é um quadrado.
3. Um prisma é um sólido formado por todos os
pontos do espaço localizados dentro dos
planos que contêm as faces laterais e os
planos das bases.
As faces laterais e as bases formam a envoltória
deste sólido. Esta envoltória é uma “superfície”
que pode ser planificada no plano cartesiano.
Tal planificação realiza-se como se cortássemos
com uma tesoura esta envoltória exatamente
sobre as arestas para obter uma região plana
formada por áreas congruentes às faces laterais
e às bases. A planificação é útil para facilitar os
cálculos das áreas lateral e total.
db = diagonal da base
Área lateral
A área lateral AL é dada pela área dos
quadrados de lado a:
AL=4a2
Área total
A área total AT é dada pela área dos seis
quadrados de lado a: AT=6a2
Volume
De forma semelhante ao paralelepípedo
retângulo, o volume de um cubo de aresta a é
dado por: V = a3
Paralelepípedo retângulo
Seja o paralelepípedo retângulo de dimensões
a, b e c da figura:
do Aprovar.
Temos quatro arestas de medida a, quatro
arestas de medida b e quatro arestas de medida
c; as arestas indicadas pela mesma letra são
paralelas.
Diagonais da base e do paralelepípedo
db = diagonal da base
Para os deficientes visuais, a prova será
aplicada na Biblioteca Braille do Estado
do Amazonas, instalada na Biblioteca
Pública (Rua Barroso, 57, Centro). Mas é
preciso agendar previamente com o sr.
Gilson Pereira pelo telefone 3234-0588.
Prepare-se e boa sorte!
a) O volume de um prisma é dado por:
V(prisma) = A(base).h
b) A área lateral de um prisma reto que tem por
base uma região poligonal regular de n lados
é dada pela soma das áreas das faces laterais.
Como nesse caso todas as áreas das faces
laterais são iguais, basta tomar a área lateral
como:
dp = diagonal do paralelepípedo
Área lateral
Sendo AL a área lateral de um paralelepípedo
retângulo, temos:
AL= ac + bc + ac + bc = 2ac + 2bc =AL =
2(ac + bc)
2
Área total
Planificando o paralelepípedo, verificamos que a
área total é a soma das áreas de cada par de
faces opostas:
AT= 2(ab + ac + bc)
Volume
Como o produto de duas dimensões resulta
sempre na área de uma face e como qualquer
face pode ser considerada como base,
podemos dizer que o volume do paralelepípedo
retângulo é o produto da área da base AB pela
medida da altura h:
resulta num octaedro. Quando as faces das
pirâmides são triângulos eqüiláteros, o
octaedro é regular.
Secção paralela à base de uma pirâmide
Um plano paralelo à base que intercepte todas
as arestas laterais determina uma secção
poligonal de modo que:
a) as arestas laterais e a altura sejam divididas
na mesma razão;
b) a secção obtida e a base sejam polígonos
semelhantes;
c) as áreas desses polígonos estejam entre si
assim como os quadrados de suas distâncias
ao vértice.
V =AB.h ⇒ V = abc
Pirâmides
Dados um polígono convexo R, contido em um
plano α, e um ponto V ( vértice) fora de α,
chamamos de pirâmide o conjunto de todos os
segmentos VP, com P∈R.
Elementos da pirâmide
Desafio
Matemático
z01.
Calcule a área lateral de um
prisma reto cuja base é um triângulo
de lados medindo 4cm, 6cm e 8cm e
cuja altura mede 2cm:
2
2
a) 24cm
2
d) 38cm
2
VA’
VB’
VC’ VD’
VE’
h
––– = ––– = ––– = ––– = ––– = –––
VA
VB
VC
VD
VE
H
2
área A’B’C’D’E’
h
–––––––––––––– = ––––
2
área ABCDE
H
Relações entre os elementos de uma
pirâmide regular
Vamos considerar uma pirâmide regular
hexagonal, de aresta lateral l e aresta da base a:
• base: o polígono convexo R
• arestas da base: os lados do polígono AB,
BC, CD, DE, EA
• arestas laterais: os segmentos VA, VB, VC,
VD, VE.
• faces laterais: os triângulos VAB, VBC, VCD,
VDE, VEA
• altura: distância h do ponto V ao plano
Classificação
Uma pirâmide é reta quando a projeção
ortogonal do vértice coincide com o centro do
polígono da base.
Toda pirâmide reta, cujo polígono da base é
regular, recebe o nome de pirâmide regular. Ela
pode ser triangular, quadrangular, pentagonal,
etc., conforme sua base seja, respectivamente,
um triângulo, um quadrilátero, um pentágono, etc.
a
MC = –––––
2
2
2
2
h =l –a
2
b) A face lateral da pirâmide é um triângulo
isósceles.
é o apótema da pirâmide (altura de uma
face lateral).
Áreas
Numa pirâmide, temos as seguintes áreas:
a) área lateral (AL): reunião das áreas das faces
laterais.
b) área da base (AB): área do polígono convexo
(base da pirâmide).
c) área total (AT): união da área lateral com a
área da base:
AT = AL +AB.
Para uma pirâmide regular, temos:
bg
AL = n. ––– AB =pa
em que:
2
b é a aresta; g é o apótema; n é o número de
arestas laterais; p é o semiperímetro da base;
a é o apótema do polígono da base.
Observações:
1.a Toda pirâmide triangular recebe o nome do
tetraedro. Quando o tetraedro possui como
faces triângulos eqüiláteros, ele é denominado
regular (todas as faces e todas as arestas são
congruentes).
Volume
O princípio de Cavalieri assegura que um cone
e uma pirâmide equivalentes possuem volumes
iguais:
2.a A reunião, base com base, de duas
pirâmides regulares de bases quadradas
3
2
b) 32cm
2
e) 26cm
c) 22cm
03. Um prisma triangular regular tem 60cm
de perímetro da base. Se o volume do
prisma é de 800
cm3, calcule a
medida da altura.
a) 6cm
d) 8cm
b) 10cm
e) 12cm
c) 4cm
04. Num paralelepípedo retângulo, o volume
é 600cm3. Uma das dimensões da base
é igual ao dobro da outra, enquanto a
altura é 12cm. Calcule as dimensões da
base desse paralelepípedo.
a) 5cm e 10cm
b) 7cm e 10cm
c) 4cm e 7cm
d) 5cm e 8cm
e) 10cm e 12cm
05. Um paralelepípedo retângulo tem
arestas medindo 5, 4 e k. Sabendo que
sua diagonal mede
, calcule k.
a) k = 6
d) k = 9
a) A base da pirâmide é um polígono regular
inscritível em um círculo de raio OB=R.
c) 36cm
02. Um prisma triangular regular tem
cm de aresta da base. Sabendo que a
medida da aresta lateral é o dobro da
medida da aresta da base, calcule a
área lateral do prisma.
a) 18cm
2
d) 16cm
Dada a pirâmide a seguir, temos os seguintes
elementos:
2
b) 34cm
2
e) 22cm
b) k = 7
e) k = 8
c) k = 5
06. Calcule a área total de um prisma reto,
de 6 metros de altura, tendo por base
um retângulo de área 12m2 e cuja
diagonal mede 5 metros.
2
2
a) 96m
2
d) 108m
2
b) 89m
2
e) 112m
c) 67m
07. Uma caixa-d’água tem forma cúbica
com 1m de aresta. Quanto baixa o
nível da água ao retirarmos 1 litro de
água da caixa?
a) 0,1cm
d) 0,4cm
b) 0,3cm
e) 0,6cm
c) 0,2cm
08. Calcule a área lateral de uma pirâmide
triangular regular, cuja aresta lateral
mede 13cm e o apótema da pirâmide
mede 12cm.
2
a) 100cm
2
d) 160cm
2
b) 110cm
2
e) 180cm
2
c) 140cm
09. Determine o volume de uma pirâmide
hexagonal regular, cuja aresta lateral
tem 10m e o raio da circunferência
circunscrita à base mede 6m.
3
a) 144m
3
d) 154m
3
b) 124m
3
e) 104m
3
c) 134m
Desafio
Matemático
Matemática
Professor CLÍCIO
Aplicação
2
a) 32cm
2
d) 30cm
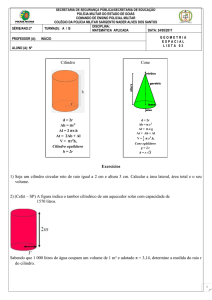
Sólidos circulares
2
b) 22cm
2
e) 32cm
c) 16cm
02. (FGV)Uma seringa tem a forma cilíndrica
com 2cm de diâmetro por 8cm de
comprimento. Quando o êmbolo se
afastar 5cm da extremidade da seringa
próxima à agulha,qual o volume,em
ml,de remédio líquido que a seringa
pode conter.
a) 15ml
d) 10ml
b) 15,7ml
e) 18,7ml
c) 14ml
2
2
2
b) 1032cm
2
e) 1234cm
c) 1024cm
04. (PUC)O raio de um cilindro circular reto
é aumentado em 25%; para que o
volume permaneça o mesmo, a altura
do cilindro deve ser diminuída em k%.
Então k vale:
a) 36
d) 30
b) 28
e) 32
c) 25
05. (PUC)Uma caixa cúbica de aresta
medindo 20cm está totalmente cheia de
mercúrio. Despeja- se o seu conteúdo
num tubo cilíndrico de 10cm de raio. A
que altura chega o mercúrio no tubo?
a) 20/cm
d) 60/cm
b) 30/cm
e) 80/cm
c) 40/cm
06. (UEA)A área lateral de um cone é
24πcm2 e o raio de sua base é 4cm.
Qual é a área total do cone?
2
a) 125,6cm
2
d) 130,8cm
2
b) 120,6cm
2
e) 120,3cm
2
c) 135,6cm
07. (UFPA) Um cone e um prisma
quadrangular regular retos têm bases
de mesma área. O prisma tem altura 12
e volume igual ao dobro do volume do
cone. Então, a altura do cone vale:
a) 18
d) 24
b) 16/3π
e) 8
c) 36
08. (UFMG) Um pedaço de cartolina possui
a forma de um semicírculo de raio 20cm.
Com essa cartolina um menino constrói
um chapéu cônico e o coloca com a
base apoiada sobre uma mesa. Qual a
distância do bico do chapéu à mesa?
a)
d) 20 cm
b)
e) 10 cm
O conceito de cilindro é muito importante. Nas
cozinhas, encontramos aplicações intensas do
uso de cilindros. Nas construções, observamos
caixas d’água, ferramentas, objetos, vasos de
plantas, todos eles com formas cilíndricas.
Classificação quanto à inclinação
Em função da inclinação do segmento AB em
relação ao plano do “chão”, o cilindro será
chamado reto ou oblíquo, respectivamente, se o
segmento AB for perpendicular ou oblíquo ao
plano que contém a curva diretriz.
2. Cones
O conceito de cone
Considere uma região plana limitada por uma
curva suave (sem quinas), fechada e um ponto
P fora desse plano. Chamamos de cone ao
sólido formado pela reunião de todos os
segmentos de reta que têm uma extremidade
em P e a outra num ponto qualquer da região.
Principais elementos
03. (FGV)Um retângulo gira em torno de
um dos seus lados, que mede 6cm.O
volume do sólido gerado por esse
retângulo é de 600cm3. Calcule a área
total desse sólido.
a) 1004,8cm
2
d) 1122cm
(UFAM) O raio de um cilindro de revolução
mede 1,5m. sabe- se que a área da base do
cilindro coincide com a área da secção
determinada por um plano que contém o eixo
do cilindro. Então, a área total do cilindro, em
2
m , vale:
a) 3π2/4
b) 9π(2 + π)/4 c) π(2 + π)
d) π2/2
e) 3π(1 + π)/2
Solução:
r = 1,5m
2
AB = AS ⇒ π r = 2rh ⇒ π r = 2h ⇒ h = 3π/4m
AT = 2π r (r + h)
AT = 2π.1,5.(1,5 + 3π/4)
AT = 9π (2 + π )/4
1. Cilindros
01. (MACK)Num cilindro, a alturaé igual ao
raio da base. Sabe- se também, que a
área lateral desse cilindro é 16cm2.
Calcule a área total do cilindro.
2
At= 2Ab + Al
At= 2.π. r2 + 2.π. r. h
At= 2.π .r (r + h)
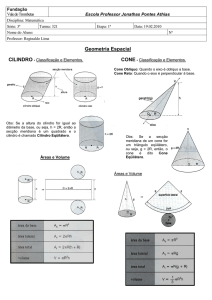
• Base: É a região plana contendo a curva
diretriz e todo o seu interior. Num cilindro
existem duas bases.
• Eixo: É o segmento de reta que liga os
centros das bases do "cilindro".
• Altura: A altura de um cilindro é a distância
entre os dois planos paralelos que contêm as
bases do "cilindro".
• Superfície Lateral: É o conjunto de todos os
pontos do espaço, que não estejam nas
bases, obtidos pelo deslocamento paralelo da
geratriz sempre apoiada sobre a curva diretriz.
• Superfície Total: É o conjunto de todos os
pontos da superfície lateral reunido com os
pontos das bases do cilindro.
• Área lateral: É a medida da superfície lateral
do cilindro.
• Área total: É a medida da superfície total do
cilindro.
• Seção meridiana de um cilindro: É uma
região poligonal obtida pela interseção de um
plano vertical que passa pelo centro do
cilindro com o cilindro.
Elementos do cone
• Base: A base do cone é a região plana
contida no interior da curva, inclusive a
própria curva.
• Vértice: O vértice do cone é o ponto P.
• Eixo: Quando a base do cone é uma região
que possui centro, o eixo é o segmento de
reta que passa pelo vértice P e pelo centro da
base.
• Geratriz: Qualquer segmento que tenha uma
extremidade no vértice do cone e a outra na
curva que envolve a base.
• Altura: Distância do vértice do cone ao plano
da base.
• Superfície lateral: A superfície lateral do cone
é a reunião de todos os segmentos de reta
que tem uma extremidade em P e a outra na
curva que envolve a base.
• Superfície do cone: A superfície do cone é a
reunião da superfície lateral com a base do
cone que é o círculo.
• Seção meridiana: A seção meridiana de um
cone é uma região triangular obtida pela
interseção do cone com um plano que
contem o eixo do mesmo.
Classificação dos cilindros circulares
• Cilindro circular oblíquo – Apresenta as
geratrizes oblíquas em relação aos planos
das bases.
• Cilindro circular reto – As geratrizes são
perpendiculares aos planos das bases. Este
tipo de cilindro é também chamado de
cilindro de revolução, pois é gerado pela
rotação de um retângulo.
• Cilindro eqüilátero – É um cilindro de revolução cuja seção meridiana é um quadrado.
Volume de um “cilindro”
Em um cilindro, o volume é dado pelo produto
da área da base pela altura.
V = A(base) h
Se a base é um círculo de raio r, e π=3,141593...,
então: V = π r² h
Classificação do cone
Área lateral e área total de um cilindro circular
reto
Quando observamos a posição relativa do eixo
em relação à base, os cones podem ser
classificados como retos ou oblíquos. Um cone é
dito reto quando o eixo é perpendicular ao plano
da base, e é oblíquo quando não é um cone
reto. Abaixo, apresentamos um cone oblíquo.
Em um cilindro circular reto, a área lateral é
dada por A(lateral)=2π.r.h, onde r é o raio da
base, e h é a altura do cilindro. A área total
corresponde à soma da área lateral com o
dobro da área da base.
c)
4
Observações sobre um cone circular reto
Um cone circular reto é chamado cone de
revolução por ser obtido pela rotação
(revolução) de um triângulo retângulo em torno
de um de seus catetos
A seção meridiana do cone circular reto é a
interseção do cone com um plano que contem o
eixo do cone. No caso acima, a seção meridiana
é a região triangular limitada pelo triângulo
isósceles VAB.
Em um cone circular reto, todas as geratrizes
são congruentes entre si. Se g é a medida de
cada geratriz então, pelo Teorema de Pitágoras,
temos: g2 = h2 + R2
A área da superfície esférica é dada por:
S = 4.π.R2
Calota esférica
É a parte da esfera gerada do seguinte modo:
A Área Lateral de um cone circular reto pode ser
obtida em função de g (medida da geratriz) e R
(raio da base do cone): ALat = π R g
A área da calota esférica é dada por:
S = 2.π.R.h
A Área total de um cone circular reto pode ser
obtida em função de g (medida da geratriz) e R
(raio da base do cone): ATotal = π . R . g + π R2
Desafio
Matemático
01. (USP)A altura e o raio da base de um
cone circular reto medem 4cm e 15cm,
respectivamente. Aumenta- se a altura
e diminui- se o raio da base desse
cone, de uma mesma medida x, x ≠ 0,
para obter- se outro cone circular reto,
de mesmo volume que o original.
Determine x em centímetros.
Fuso esférico
a) 2cm
b) 3cm
O fuso esférico é uma parte da superfície
esférica que se obtém ao girar uma semicircunferência de um ângulo (0< x <2π )em
torno de seu eixo:
d) 5cm
e) 6cm
02. (USP)O volume de um cone é 400m3 e
o raio de sua base é 5m. Calcule a área
lateral desse cone.
2
a) 230,5m
2
d) 222,5m
Aplicação
c) 4cm
2
b) 241,5m
2
c) 225,5m
2
e) 240,5m
03. (PUC-SP) Qual é o raio de uma esfera
1milhão de vezes maior (em volume)
que uma esfera de raio 1?
Os catetos de um triângulo retângulo medem b
2
e c e a sua area mede 2m . O cone obtido pela
rotação do triângulo em torno do cateto b tem
3
volume 16πm . Determine o comprimento do
cateto c.
A área do fuso esférico pode ser obtida por uma
regra de três simples:
As → 2π
2
⇒ Af= 2R α (α em radianos)
Af → α
As → 360°
Solução:
2
Como a área do triangulo mede 2m , segue que
(1/2)bc = 2, implicando que b.c = 4.
V =(1/3) Abase h
2
16π R b
16π = (1/3) πc.c.b
16 = c(4/3)
c = 12 m
Af → α
2
πR α
⇒ Af= ––––– (α em graus)
90°
Parte da esfera que se obtém ao girar um semicírculo em torno de seu eixo de um ângulo
α (0< α <2π ):
d) 2
e)2
Aplicação
Superfície esférica
A superfície esférica de centro O e raio R é o
conjunto de pontos do espaço cuja distância ao
ponto O é igual ao raio R.
Se considerarmos a rotação completa de uma
semicircunferência em torno de seu diâmetro, a
superfície esférica é o resultado dessa rotação.
5
c) 10 000
04. (UFMG) Duas bolas metálicas, cujos
raios medem 1cm e 2cm, são fundidas
e moldadas em forma de um cilindro
circular cuja altura mede 3cm. O raio
do cilindro, em cm, é:
b) 2
Seja 36π o volume de uma esfera circunscrita a
um cubo. Então, a razão entre o volume da
esfera e o volume do cubo é:
a) 8π/3
b) 2π/3
c) π/4
π
e) π/2
d)
Solução:
Partes da esfera
e) 100
a) 3/2
O volume da cunha pode ser obtido por uma
regra de três simples:
Volume
O volume da esfera de raio R é dado por:
4
3
V = –– .πR
3
b) 10
d) 1 000
Cunha esférica
3. Esferas
Chamamos de esfera de centro O e raio R o
conjunto de pontos do espaço cuja distância ao
centro é menor ou igual ao raio R.
Considerando a rotação completa de um
semicírculo em torno de um eixo e, a esfera é o
sólido gerado por essa rotação. Assim, ela é
limitada por uma superfície esférica e formada
por todos os pontos pertencentes a essa
superfície e ao seu interior.
a) 100 000
c) 6
05. (UFPE) Uma esfera de centro O e raio
igual a 5cm é cortada por um plano P,
resultando desta interseção uma
circunferência de raio igual a 4cm.
Assinale, então, a alternativa que
fornece a distância de O a P.
a) 10cm
b) 5cm
d) 1cm
e) 3cm
c) 2cm
06. (UFPA) O círculo máximo de uma
esfera mede 6πcm. Qual o volume da
esfera?
3
3
3
a) 12πcm
b) 24πcm
d) 72πcm
e) 144πcm
3
3
c) 36πcm
07. (UFRS) Uma panela cilíndrica de 20cm
de diâmetro está completamente cheia
de massa para doce, sem exceder a
sua altura de 16cm. O número de
doces em formato de bolinhas de 2cm
de raio que se podem obter com toda a
massa é:
a) 300
b) 250
d) 150
e) 100
c) 200
Desafio
Físico
Física
Professor CARLOS Jennings
Eletrodinâmica I
Leis de OHM
01. (Desafio da TV) Um chuveiro de 2400W,
funcionando 4 horas por dia durante 30
dias, consome a energia elétrica, em
kWh, de:
a) 288
d) 288.000
b) 320
e) 0,32
c) 18.000
02. (UFPE) Alguns cabos elétricos são feitos
de vários fios finos trançados e
recobertos com um isolante. Um certo
cabo tem 150 fios e a corrente total
transmitida pelo cabo é de 0,75A
quando a diferença de potencial é 220V.
Qual é a resistência de cada fio
individualmente, em kΩ?
03. (Unifesp) A linha de transmissão que
leva energia elétrica da caixa de relógio
até uma residência consiste de dois fios
de cobre com 10,0m de comprimento e
seção reta com área 4,0mm2 cada um.
Considerando que a resistividade
elétrica do cobre é ρ = 1,6 . 10-6Ω.m:
a) calcule a resistência elétrica r de
cada fio desse trecho do circuito.
b) Se a potência fornecida à residência
for de 3.300W a uma tensão de 110V,
calcule a potência dissipada P nesse
trecho do circuito.
04. (UFRS) Quando uma diferença de
potencial é aplicada aos extremos de
um fio metálico, de forma cilíndrica, uma
corrente elétrica i percorre esse fio. A
mesma diferença de potencial é
aplicada aos extremos de outro fio, do
mesmo material, com o mesmo
comprimento mas com o dobro do
diâmetro. Supondo os dois fios à
mesma temperatura, qual será a
corrente elétrica no segundo fio?
a) i
d) 4 i
b) 2 i
e) i / 4
c) i / 2
05. (Cesgranrio) O gráfico a seguir
representa as intensidades das
correntes elétricas que percorrem dois
resistores ôhmicos R1 e R2 em função
da ddp aplicada em cada um deles.
Abaixo do gráfico, há o esquema de um
circuito no qual R1 e R2 estão ligados
em série a uma fonte ideal de 12V.
Neste circuito, a intensidade, da
corrente elétrica que percorre R1 e R2
vale:
a) 0,8A
d)1,5A
b) 1,0A
e) 1,8A
a) Qual a intensidade e o sentido da corrente
elétrica i4 no fio 4?
b) Quantos elétrons passam por uma seção
transversal do fio 4 em cada segundo? (carga
–19
elétrica elementar = e = 1,6 . 10 C).
Solução:
a) A soma das correntes que chegam ao nó é
igual à soma das que saem dele. Saindo do
nó temos:
i2 + i3 = 15A+ 21A = 36A
Chegando ao nó:
i1 = 20A
Então, pelo fio 4 deve chegar uma corrente
i4 = 16A, para totalizar também 36A.
b)16A = 16C/s
–19
1,6 . 10 C → 1 elétron
16C → n elétrons
20
n = 1,0 . 10
Corrente elétrica – É o movimento ordenado de
portadores de carga elétrica, ou seja, um fluxo
de portadores de carga num determinado
sentido.
Gerador elétrico
Diz-se de todo sistema capaz de gerar correntes
elétricas, operando para converter alguma
modalidade de energia não-elétrica em energia
elétrica. Pilhas, baterias e usinas hidroelétricas
são exemplos de geradores.
Intensidade da corrente elétrica
Seja Q a soma dos módulos de todas as cargas
que atravessam uma seção transversal de um
condutor, num certo intervalo de tempo:
Diferença de potencial elétrico (ddp)
Considere o fio metálico representado abaixo,
cujas extremidades estão ligadas ao pólo de um
gerador. Entre elas, existe uma diferença de
potencial (ddp) ou tensão elétrica, cujo valor
absoluto vamos representar por U.
A intensidade i da corrente elétrica nesse
condutor é definida por:
Q
i = –––
∆t
Unidade no SI: C/s = ampère = A.
Uma intensidade de corrente de 10A, por
exemplo, significa que passam 10C de carga
pela seção em cada segundo.
Sentido convencional da corrente elétrica
O sentido que se convencionou para a corrente
elétrica no condutor é o sentido dos potenciais
decrescentes, como indica a figura anterior.
Note que esse sentido é oposto ao sentido real
do movimento dos elétrons livres. No caso de
portadores móveis positivos (como íons
positivos em soluções eletrolíticas), o sentido do
movimento dos portadores coincide com o
sentido convencional.
A ddp indica:
• a energia potencial elétrica que cada coulomb
de carga entrega ao fio na forma de energia
térmica, quando se desloca pelo fio, de uma
extremidade à outra;
Ou
• a energia potencial elétrica que o gerador
repõe em cada coulomb de carga que se
desloca pelo gerador, de um terminal a outro.
Se, num certo intervalo de tempo, o fio recebe do
gerador uma quantidade de energia elétrica E, a
potência elétrica Pot, consumida ou dissipada
pelo fio (ou fornecida pelo gerador), é dada por:
E
Pot =––––
∆t
Unidade no SI: J/s = watt = W.
Uma lâmpada operando numa potência de
100W, por exemplo, consome 100J de energia
elétrica em cada segundo.
Por outro lado, se há uma ddp igual a U volts
entre as extremidades do fio, isso significa que 1
coulomb de carga entrega ao fio U joules de
energia. Se, num certo intervalo de tempo,
passa uma carga de módulo Q coulombs pelo
fio, a energia E entregue a ele será:
1 coulomb → U joules
Q coulombs → E joules
E=Q.U
Então:
E
Q.U
Q
Pot =–––– = –––– = U. ––– ⇒ Pot = U. i
∆t
∆t
∆t
Relação entre as correntes elétricas em um nó
Nó é o ponto de um circuito elétrico em que
mais de dois fios condutores estão interligados
(ponto P da figura abaixo).
Em qualquer intervalo de tempo, a quantidade
de elétrons que chega ao nó é igual à que sai
dele. Então, a soma das intensidades das
correntes elétricas que chegam ao nó também é
igual à soma das que dele saem:
i1 + i 2 = i 3 + i 4
Aplicação
Quilowatt-hora (kWh)
É uma importante unidade de medida de
energia. Equivale à energia consumida, por
exemplo, por um aparelho que opera com
potência de 1kW durante 1h.
3
6
1kWh = 1kW . 1h = 10 W . 3600s = 3,6 . 10 J
A figura mostra quatro fios condutores
interligados no ponto P. Em três desses fios,
estão indicados os sentidos (convencionais) das
correntes elétricas:
Resistência elétrica
Considere um condutor submetido a uma
diferença de potencial U e percorrido por uma
corrente elétrica de intensidade i:
c) 1,2A
i1 = 20A, i2 = 15A e i3 = 21A (constantes).
6
Sua resistência elétrica R é definida por:
U
R = ––––
i
Unidade no SI: V/A = ohm = Ω.
Se a resistência elétrica de um fio metálico é,
por exemplo, igual a 5Ω, são necessários 5V
para produzir cada ampère de corrente. Assim,
no SI, a resistência informa quantos volts são
necessários para produzir 1A nesse fio.
Em esquemas de circuitos, a resistência elétrica
é simbolizada por:
Em esquemas de circuitos, um resistor é
simbolizado por:
A potência dissipada no resistor é a energia
elétrica que nele se converte em energia térmica
por unidade de tempo. Como já sabemos, essa
energia é dada por:
Pot = U . i
Mas como U = R . i:
Pot = R . i . i ⇒ Pot = R . i2
U
Como i = –––:
R
2
U
U
Pot = U. ––– = ⇒ Pot =–––
R
R
Condutor ideal
Diz-se de todo condutor cuja resistência elétrica
é igual a zero. Seu símbolo em esquemas de
circuitos é:
Entre os terminais de um condutor ideal, a
diferença de potencial é igual a zero, seja ele
percorrido por corrente ou não.
Mas é bom que se diga: excluindo o fenômeno
da supercondutividade, não existe condutor
ideal. Há, entretanto, condutores cujas resistências podem ser desprezadas em relação a
outras: os fios de cobre usados na instalação de
uma lâmpada, por exemplo, têm resistências
desprezíveis em comparação com a da lâmpada.
Os fusíveis de proteção de circuitos e os
interruptores também possuem resistências
desprezíveis.
Símbolos de um interruptor simples:
Segunda Lei de Ohm
Considere um condutor de comprimento L e
seção transversal uniforme de área A. A
resistência elétrica R desse condutor é
diretamente proporcional ao seu comprimento
L, e inversamente proporcional à área A. Sendo
ρ uma constante de proporcionalidade
denominada resistividade elétrica ou resistência
específica do material que constitui o condutor,
temos:
L
R = ρ. ––––
A
Ao se estabelecer uma corrente no condutor, L
é a distância percorrida pelos portadores de
carga livres, e A é a área através da qual eles
fluem. Numericamente, no SI, o valor de ρ é
igual ao da resistência de um condutor em que
2
L = 1m e A = 1m .
Da expressão anterior, temos:
A
ρ = R. ––––
L
2
Unidade de ρ no SI: Ω . m /m = Ω . m
2
Unidade prática de ρ: Ω . mm /m
Interruptor aberto (não passa corrente: i = 0).
Interruptor fechado (passa corrente: i ¹ 0).
Símbolo de um fusível:
Se um fusível for de 30A, por exemplo, ele
deverá queimar quando passar ele uma corrente
i superior a 30A. Ao queimar, o circuito ficará
aberto e teremos i = 0.
Valores nominais
Reostato
Valores nominais de um aparelho elétrico
(lâmpada, chuveiro, ferro de passar roupa, etc.)
são os valores de tensão e potência especificados pelo seu fabricante para que funcione
corretamente. Considere, por exemplo, uma
lâmpada cujos valores nominais são: 100W –
220V. Isso significa que ela opera com potência
de 100W desde que seja ligada a 220V.
É um resistor de resistência variável (ajustável
mecanicamente). Por exemplo, quando giramos
o potenciômetro de volume de um rádio, aumentamos ou diminuímos uma certa corrente elétrica,
e, assim, aumentamos ou diminuímos o volume
do som. Veja detalhes internos de um potenciômetro:
CONDUTORES ÔHMICOS
Primeira Lei de Ohm
Para alguns condutores (metais e grafite, por
exemplo), mantidos em temperaturas constantes,
a ddp U e a intensidade de corrente i são
diretamente proporcionais. A constante de
proporcionalidade é a sua resistência R:
U
––– = constante = R
i
Podemos escrever também:
U = R . i (sendo R constante em temperatura
constante).
O cursor é uma pequena haste metálica em
contato com a película de grafite. Dependendo
da posição do cursor, a corrente elétrica percorrerá uma parte mais longa ou menos longa
dessa película. Assim, para cada posição do
cursor, o potenciômetro terá uma resistência
elétrica diferente.
Em esquemas de circuitos, um reostato é
simbolizado por:
Curva característica de um condutor ôhmico
Gráfico que relaciona a intensidade de corrente i
no condutor com a ddp U entre seus terminais.
Resistores
São condutores em que a energia elétrica
converte-se exclusivamente em energia térmica.
Essa conversão (dissipação) é denominada
efeito Joule.
7
Caiu no
Vestibular
Caiu no vestibular
01. (UEA) Um chuveiro submetido a uma tensão
U = 220V opera com potência Pot = 4400W.
Calcule:
a) a intensidade de corrente no chuveiro;
b) a resistência elétrica do resistor do chuveiro
em funcionamento;
c) a energia elétrica E consumida pelo chuveiro
em 15 minutos de funcionamento, em J e em
kWh.
Solução:
a) Pot = U . i
4400 = 220 . i ⇒ i = 20A
b)U = R . i
220 = R . 20 ⇒ R = 11Ω
Ou:
Pot = R2 . i
4400 = R . 202 ⇒ R = 11Ω
Ou ainda:
2
U
Pot =–––
R
2
220
4400 = –––– ⇒ R = 11Ω
R
c) Pot = 4400W = 4,4kW
∆t = 15min = 900s = 1/4 h
E
Pot = ––––
∆t
E = Pot . ∆t
6
E = 4400W . 900s = 3,96 . 10 J
Ou:
E = 4,4kW . 1/4 h = 1,1kWh
Observe que é muito mais simples calcular o
consumo em kWh.
02. (UEA) Um fio de cobre sem a cobertura
isolante (desencapado) tem seção transversal
2
de área A = 6,0mm e é percorrido por uma
corrente elétrica de intensidade i = 30A. O
-2
cobre possui resistividade ρ = 1,8 . 10 Ω.
2
mm /m. Considere dois pontos, P e Q, desse
fio, separados por 10cm:
Calcule a diferença de potencial entre P e Q.
Solução:
A resistência elétrica entre P e Q, aplicando a
Segunda Lei:
L
RPQ = ρ. ––––
A
–2
10.10 m
–2
2
RPQ = 1,8.10 mm /m. ––––––––––
2
6,0mm
4
RPQ = 3,0 . 10 Ω
Agora, calculemos UPQ pela Primeira Lei:
4
UPQ = RPQ . i = 3,0 . 10 . 30
–3
UPQ = 9,0 . 10 V
Caiu no
Vestibular
Na montagem, temos três resistores de resistências
R1 = 100Ω, R2 = 30Ω, R3 = 60Ω, um reostato de
resistência R4 (variável de 0 a 80Ω) e um fio ideal F.
a) Determine a resistência equivalente RAB entre
os terminais A e B, considerando R4 = 80Ω.
b) Determine a intensidade de corrente elétrica
em R1, R2 e R3, quando é aplicada uma ddp U
= 300V entre A e B, com R4 = 0.
Solução:
a) Como as extremidades de um fio ideal estão no
mesmo potencial, associando uma letra a cada
nó, cuidando para que nós interligados por um fio
ideal recebam a mesma:
Em seguida, marcamos todos os pontos que
receberam letras, sem repetição, mantendo os
terminais em posições extremas.
Agora, redesenhamos o esquema, observando que
(na figura 1) R1 está entre A e B, R2 está entre B e
C, R3 está entre C e B, e R4, entre A e C.
30.60
R2.R3
RCB = ––––––––
= –––––– ⇒ RCB = 20Ω
R 2 + R3
30+60
Física
R
Req = ––––
n
• A resistência equivalente à de uma
associação de resistores em paralelo é menor
que a menor das resistências associadas.
Professor CARLOS Jennings
3. Associação mista:
Associação mista é aquela em que existem
resistores associados em série e em paralelo,
como na associação esquematizada abaixo:
Eletrodinâmica II
Associação de Resistores
1. Em série:
Resistores estão associados em série quando
estão interligados de modo a estabelecer um
único caminho para a corrente elétrica. Assim, a
corrente que passa por um deles é a mesma que
passa pelos demais. Esse tipo de associação é
freqüentemente utilizado na iluminação de
árvores de natal.
Consideremos n resistores de resistências R1, R2,
..., Rn associados em série. Estabelecendo uma
ddp U entre os terminais A e B da associação, os
resistores são percorridos por uma mesma
corrente de intensidade i e ficam submetidos à
ddp U1, U2, ..., Un, respectivamente, sendo cada
uma delas uma parte de U.
Resistência equivalente à da associação (Req)
é aquela que um único resistor deveria ter para
que a mesma ddp U produzisse nele uma
corrente de mesma intensidade.
Curto-circuito
Dois pontos estão em curto-circuito quando
existe um condutor ideal conectado entre eles. A
ddp entre esses dois pontos é igual a zero. Por
isso, em cálculos de circuitos, os dois pontos
podem ser considerados coincidentes.
GERADOR ELÉTRICO EM CIRCUITOS
Grandezas características de um gerador
elétrico
Quando um gerador não participa de um
circuito, ou seja, quando ele não é percorrido
por uma corrente elétrica, existe entre seus
terminais (pólos), A e B, uma ddp ε,
denominada “força” eletromotriz (fem). No
caso das pilhas comuns, ε = 1,5V, e, no caso
de baterias de automóvel, ε = 12V. É bom que
se diga: a denominação de “força” eletromotriz
é inadequada, pois não se trata de força, mas
de energia por unidade de carga.
Como todo condutor real, o gerador apresenta
uma resistência elétrica r, denominada
resistência interna do gerador.
Então:
A intensidade de corrente i é igual em todos os
resistores.
U = U1 + U2 + ...+ Un
Req . i = R1 . i + R2 . i+ ...+ Rn . i
Req = R1 + R2 + ...+ Rn (resistência equivalente
entre os pontos A e B).
2. Em paralelo:
Resistores estão associados em paralelo
quando estão interligados de modo a se
submeterem a uma mesma ddp U,
estabelecendo mais de um caminho para a
corrente elétrica. Esse tipo de associação é
usado, por exemplo, na iluminação de uma
residência.
Consideremos n resistores de resistências R1,
R2, ..., Rn associados em série. Estabelecendo
uma ddp U entre os terminais A e B da
associação, a ddp será igual a U em todos os
resistores, e neles serão estabelecidas correntes
elétricas de intensidades i1, i2, ..., in:
Circuito simples
Assim denomina-se um circuito em que um
gerador alimenta um resistor.
80Ω + 20Ω = 100Ω
Essa resistência de 100Ω está em paralelo com
R1, que também é igual a 100Ω :
100
100
RAB = ––––– = ––––– ⇒ RAB = 50Ω
n
2
b) R4 = 0 significa que o reostato tornou-se um
condutor ideal:
Redesenhando o esquema, temos:
O gerador estabelece entre os terminais do
resistor uma ddp U que é menor que a força
eletromotriz ε, como veremos adiante. Note que
o sentido (convencional) da corrente é de (–)
para (+) dentro do gerador, e de (+) para (–)
fora dele, ou seja, é de (+) para (–) no resistor.
Generalizando a informação:
Elementos em que a corrente passa de (–) para
(+) estão fornecendo energia elétrica (são os
geradores).
Elementos em que a corrente passa de (+) para
(–) estão recebendo energia elétrica (são os
resistores e os receptores).
Então:
A ddp U é igual em todos os resistores.
i = i1 + i2 + ... + in
U
U
U
U
–––– = –––– + –––– + ... + –––– ⇒
Req
R1
R2
Rn
1
1
1
1
⇒ –––– = ––– + –––– + ... + ––––
Req
R1
R2
Rn
Essa expressão dá a resistência equivalente
entre os pontos A e B.
Anote aí:
U = R1 . i1 → 300 = 100 . i1 → i1 = 3A
U = R2 . i2 → 300 = 30 . i2 → i2 = 10A
U = R3 . i3 → 300 = 60 . i3 → i3 = 5A
• Cálculo prático para apenas dois resistores
em paralelo:
R1.R2
Req = –––––––––
R 1 + R2
• n resistores de resistências iguais a R, em
paralelo:
Anote aí: quando um gerador alimenta dois ou
mais resistores, temos um circuito que pode ser
reduzido a um circuito simples, bastando
calcular a resistência equivalente à da
associação dos vários resistores alimentados.
8
Equação do gerador
U
também η = –––)
ε
Gerador ideal
Diz-se de um gerador hipotético cuja resistência
interna r é igual a zero. É simbolizado por:
U=ε–r.i
U = ddp aproveitada pela lâmpada.
ε = ddp gerada.
r . i = ddp “perdida” dentro do gerador.
Nesse gerador não há desperdício de energia,
por isso, seu rendimento é igual a 1, ou seja,
100%.
Anote aí: na resolução de exercícios, muitas
vezes somos obrigados a considerar o gerador
ideal, quando não temos informação sobre sua
resistência interna.
Potências no gerador
Potd: é a potência elétrica desperdiçada pelo
gerador, em razão de sua resistência interna.
Significa quantos joules de energia elétrica são
dissipados inutilmente dentro do gerador, em
cada segundo.
2
Potd = r . i
Potu: é a potência elétrica útil do gerador, ou
seja, a potência que o gerador fornece a quem
ele alimenta. Significa quantos joules de energia
elétrica o gerador efetivamente fornece, em
cada segundo.
Potu = U . i
Pott: é a potência elétrica total produzida pelo
gerador, obtida pela soma da potência útil com
a desperdiçada. Significa quantos joules de
algum tipo de energia (química, no caso das
pilhas) são transformados em energia elétrica,
em cada segundo.
Pott = Potu + Potd = U . i + r . i2
Pott = (U + r . i) . i → Pott = ε . i
Associação de geradores
Desafio
Físico
01. Determine o gerador equivalente entre
os pontos A e B:
1. Em série:
O pólo positivo de um gerador é ligado ao pólo
negativo do gerador seguinte. Considere n
geradores de forças eletromotrizes ε1, ε2, ..., εn,
e resistências internas r1, r2, ..., rn, respectivamente, associados em série:
Sendo εeq e req a força eletromotriz e
resistência interna do gerador equivalente à
associação, temos:
εeq = ε1 + ε2 + ...+ εn
req = r1 + r2 +... + rn
2. Em paralelo:
Os pólos positivos dos geradores são ligados
juntos, o mesmo ocorrendo com os pólos
negativos. Considere n geradores iguais, cada
um deles com força eletromotriz ε e resistência
interna r, associados em paralelo.
Rendimento elétrico de um gerador
É a grandeza adimensional (sem unidade,
porque resulta da razão entre grandezas de
mesma natureza) ç que informa qual a fração
da potência total é aproveitada como potência
útil.
U.i
U
Pot
η = ––––u = ––––
(0 ≤ η < 1)
ε .i = ––––
ε
Pott
Intensidade de corrente elétrica num circuito
simples
Num circuito simples, temos:
No gerador: U = ε – r . i
No resistor: U = R . i
Então: ε – r . i = R . i → ε = (R + r) . i
ε = Σ Resistências . i
A resistência R pode ser a resistência equivalente
à associação de uma quantidade qualquer de
resistores.
Sendo εeq e req a força eletromotriz e
resistência interna do gerador equivalente à
associação, temos:
εeq = ε
r
req = –––
n
Anote aí: na prática, não é comum associar, em
paralelo, geradores de diferentes forças
eletromotrizes, porque podemos ter geradores
alimentando outros geradores. Os alimentados
funcionariam como receptores elétricos.
Aplicação
Um gerador de fem ε = 12V, e resistência
interna r = 1Ω está ligado a um resistor de
resistência R = 3Ω.
Vantagens e desvantagens das associações
de geradores
Nas associações (I) e (II), cada pilha tem "força"
eletromotriz e e resistência interna r.
Calcule:
a) a intensidade da corrente elétrica no circuito;
b) a ddp U entre os terminais do gerador (ou do
resistor, pois é a mesma);
c) a potência útil do gerador;
d) a potência desperdiçada dentro do gerador;
e) a potência elétrica total gerada;
f) o rendimento elétrico do gerador.
Solução:
a) ε = Σ Resistências . i
12 = (3 + 1) . i → i = 3A
b)No gerador: U = ε – r . i = 12 – 1 . 3 = 9V
Ou no resistor: U = R . i = 3 . 3 = 9V
c) Potu = U . i = 9 . 3 = 27W (poderia ser
2
2
também R . i ou U /R)
2
2
d)Potd = r . i = 1 . 3 = 9W
e) Pott = ε . i = 12 . 3 = 36W (poderia ser
também Potu + Potd)
Potu
27
= ––– = 0,75 = 75% (poderia ser
f) η = –––––
Pott
36
Vamos discutir a vantagem e a desvantagem de
cada uma:
Em (I), as pilhas estão associadas em série.
Então:
εeq = ε1 + ε2 + ...+ εn
εeq = ε + ε + ε → εeq = 3ε (vantagem:
multiplica a força eletromotriz).
req = r1 + r2 +... + rn
req = r + r + r → req = 3r (desvantagem:
aumenta a resistência interna).
Em (II), as pilhas estão associadas em paralelo:
εeq = ε (desvantagem: mantém a força
eletromotriz dos geradores associados).
r
r
req = ––– → req = ––– (vantagem: diminui a
n
3
resistência interna).
9
Caiu no vestibular
Calcule a resistência R para que a resistência
equivalente entre A e B seja RAB = 35Ω.
Solução:
As resistências de 10Ω, 20Ω e 30Ω estão em série,
uma vez que são atravessadas pela mesma
corrente elétrica.
Essas resistências equivalem a:
10Ω + 20Ω + 30Ω = 60Ω
As resistências de 40Ω e 60Ω estão em paralelo
porque se ligam aos mesmos pontos, C e D,
estando submetidas à mesma ddp. A resistência
equivalente é dada por:
1
1
1
–––– = ––– + –––– ⇒ RCD = 24Ω
RCD
40
60
Poderíamos também usar o cálculo prático para
dois resistores em paralelo:
40.60
2400
RCD = ––––––– = –––––– ⇒ RCD = 24Ω
40+60
100
As três resistências que restaram estão em série:
RAB = R + 24 + 1
Como RAB = 35Ω:
35 = R + 24 + 1→ RAB = 10Ω
Desafio
literário
01. (Desafio do Rádio) Identifique o
autor do excerto de poema seguinte.
Longe do estéril turbilhão da rua,
Beneditino, escreve! No aconchego
Do claustro, na paciência e no sossego,
Trabalha, e teima, e lima, e sofre, e sua!
a)
b)
c)
d)
e)
Castro Alves
Alberto de Oliveira
Raimundo Correia
Olavo Bilac
Francisca Júlia
02. Leia as informações seguintes. Opte,
depois, pela alternativa coerente.
I
Olavo Bilac, apesar de ser considerado
um poeta parnasiano, apresenta
pequenos traços românticos.
II A fama de Raimundo Correia provém
mais dos sonetos antológicos (As
Pombas, Mal Secreto) do que do
sucesso de obras poéticas publicadas.
III Vicente de Carvalho ficou conhecido
pelo epíteto de “Poeta do Mar”.
a)
b)
c)
d)
e)
Todas são verdadeiras.
Todas são falsas.
São verdadeiras apenas a I e a III.
São verdadeiras apenas a I e a II.
Apenas a I é verdadeira.
03. (Desafio da TV) Somente uma das
afirmações abaixo não se aplica ao
Parnasianismo.
a) Concepção objetiva da vida.
b) Busca da perfeição formal.
c) Valorização de elementos da mitologia
grega.
d) Espiritualismo e misticismo.
e) Apego excessivo à métrica e à rima.
04. Leia a estrofe seguinte:
“Se se pudesse, o espírito que chora,
Ver através da máscara da face,
Quanta gente, talvez que inveja agora
Nos causa, então piedade nos causasse!”
(Raimundo Correia, Mal Secreto)
Assinale a alternativa que exprime a
oposição fundamental desse quarteto.
a)
b)
c)
d)
e)
Matéria versus espírito.
Infelicidade versus felicidade.
Piedade versus falsidade.
Essência do ser versus aparência.
Tristeza versus alegria.
05. A que período da Literatura Brasileira
o texto seguinte faz referência?
“A poesia com gosto refinado, mostrando
perfeição, agradou o público leitor
brasileiro da época. Prova disso é a
extensão da influência do período: não
desapareceu nem com as primeiras
manifestações modernistas.”
a)
b)
c)
d)
e)
Pré-Modernimso.
Simbolismo.
Romantismo.
Parnasianismo.
Realismo.
Literatura
3. AUTORES E OBRAS
ALBERTO DE OLIVEIRA
Nascimento e morte – Antônio Mariano
Alberto de Oliveira nasce em Palmital de
Saquarema (RJ), em 28 de abril de 1857.
Falece em Niterói (RJ), em 19 de janeiro de
1937.
Professor João BATISTA Gomes
Parnasianismo
Popularidade – Alberto de Oliveira, demonstrando a um só tempo talento e técnica na
arte de compor versos, torna-se um dos mais
populares poetas da literatura brasileira.
1. ASPECTOS GERAIS
Cronologia – Cronologicamente, o Parnasianismo dura no Brasil de 1880 a 1893. A
influência do movimento, entretanto, ultrapassa a primeira fase do Modernismo (1922 a
1930).
Atividades profissionais – Para sobreviver
(a situação de escritor profissional é sonho
na época), Alberto torna-se farmacêutico e
professor. Diploma-se em Farmácia, em 1884,
e cursa a Faculdade de Medicina até o terceiro ano, onde se torna amigo de Olavo Bilac.
Início no Brasil – As primeiras obras do Parnasianismo brasileiro são:
Estréia – Em 1878, estréia em livro, com as
Canções Romântiicas, mostrando-se ainda
preso aos cânones do Romantismo.
a) Sonetos e Rimas (poesias, 1880), de Luís
Guimarães Júnior.
b) Fanfarras (poesias, 1882), de Teófilo Dias.
Melhor livro – Nas páginas de Meridionais
(1884), está o seu momento mais alto no que
concerne à ortodoxia parnasiana, concretizando-se o forte pendor pelo objetivismo e pelas
cenas exteriores.
Poesia realista – A denominação “poesia
realista” não vinga. Por influência européia,
dá-se o nome Parnasianismo à produção
poética do Realismo-Naturalismo.
Oposição ao Romantismo – As manifestações poéticas durante a vigência do Realismo-Naturalismo opõem-se radicalmente ao
Romantismo.
Trindade parnasiana – Com Raimundo Correia e Olavo Bilac, constitui a trindade parnasiana no Brasil.
Príncipe dos poetas – No concurso organizado pela revista Fon-Fon, em 1924, é eleito
“Príncipe dos Poetas Brasileiros”.
Origem – O movimento parnasiano surge na
França, com a publicação de uma série de
antologias denominada Parnaso Contemporâneo. Por meio delas, prega-se um modo
novo de fazer poemas: sem a emoção e sem
o subjetivismo da época romântica.
OBRAS
1.
2.
3.
4.
Origem do nome – O nome Parnasianismo
é inspirado na mitologia grega. Parnaso é o
monte consagrado a Apolo (o deus da beleza) e às musas (divindades inspiradoras da
poesia).
Canções românticas (poesias,1878)
Meridionais (poesias, 1884)
Sonetos e poemas (poesias, 1885)
Versos e rimas (poesias, 1895)
Sonetos famosos:
1. Vaso Grego
2. Vaso Chinês
Cultura grega – Tomando a cultura grega
como modelo, os parnasianos retornam à
época clássica. Fugem, assim, da influência
romântica e adotam uma linguagem menos
brasileira, com gosto por termos rebuscados
e eruditos.
RAIMUNDO CORREIA
Nascimento e morte – Raimundo da Mota
de Azevedo Correia nasce em 13 de maio
de 1859, a bordo do navio brasileiro São Luís,
ancorado na baía de Mogúncia (MA). Falece
em Paris, França, em 13 de setembro de
1911.
Influência duradoura – A poesia com gosto
refinado, mostrando perfeição, agrada o público leitor brasileiro da época. Prova disso é
a extensão da influência parnasiana: não
desaparece nem com as primeiras manifestações modernistas.
Faculdade – Na Faculdade de Direito de São
Paulo, conhece Raul Pompéia, Teófilo Dias,
Eduardo Prado, Afonso Celso, Augusto de
Lima, Valentim Magalhães, Fontoura Xavier –
todos destinados a ser grandes figuras das
letras, do jornalismo e da política.
2. CARACTERÍSTICAS DO
PARNASIANISMO
Arte pela arte – É a arte pelo simples prazer
de fazer arte, sem a influência dos sentimentos, das emoções.
Estréia – Começa na literatura em 1879, com
o volume de poesias Primeiros sonhos, experiência ainda romântica.
Perfeição formal – O poeta busca, a qualquer custo, a perfeição exterior dos poemas.
Passam a ter valor os seguintes aspectos:
As Pombas – Em 1883, publica as Sinfonias,
em cujas páginas se encontra um dos mais
conhecidos sonetos da língua portuguesa:
As Pombas.
a) rimass ricas e raras;
b) vocabulário erudito, às vezes técnicocientífico;
c) composição de soneto (2 quartetos e 2
tercetos);
d) clareza e lógica;
e) poesia descritiva;
f) ausência de emoção.
OBRAS
1.
2.
3.
4.
Primeiros Sonhos (poesias, 1879)
Sinfonias (poesias, 1883)
Versos e Versões (poesias, 1887)
Aleluias (poesias, 1891)
Sonetos famosos:
Retomada do Classicismo – Valoriza-ção
da cultura grega, com referência a obras de
arte e a nomes de deuses.
1. As Pombas
2. Mal Secreto
3. Anoitecer
Amor carnal e erótico – O amor, ao contrário
da postura ingênua adotada no Romantismo,
ganha o erotismo. Os poemas falam da nudez feminina, destacando partes do corpo
da mulher cuja descrição era proibida no período anterior.
OLAVO BILAC
Nascimento e Morte – Olavo Braz Martins
dos Guimarães Bilac nasce no Rio de Janeiro (RJ), em 16 de dezembro de 1865, onde
Falece, em 28 de dezembro de 1918.
Impassibilidade – O poeta tenta abster-se do
sentimento, da emoção, preocupando-se mais
com os aspectos técnicos da composição.
Medicina – Matricula-se na Faculdade de Medicina do Rio de Janeiro, mas é expulso no
quarto ano, acusado de necrofilia. Tenta, a
10
seguir, o curso de Direito em São Paulo, mas
não passa do primeiro ano.
Jornalista e poeta – Dedica-se, desde cedo,
ao jornalismo e à literatura. Tem intensa participação na vida política do Brasil e em campanhas cívicas, das quais a mais famosa é
em favor do serviço militar obrigatório.
Perseguido por Floriano – Fazendo jornalismo político nos começos da República, é
um dos perseguidos por Floriano Peixoto.
Briga com Pompéia – Fica famosa a briga
entre Olavo Bilac e Raul Pompéia. Os dois
chegam a comparecer em praça pública para
um duelo de espadas, que, felizmente, não
acontece.
Estréia – Publica a primeria obra em 1888,
Poesias, tornando-se o mais típico dos parnasianos brasileiros. Na obra, encontram-se os
famosos sonetos de Via-Láctea e a antológica Profissão de Fé, na qual codifica o seu
credo estético, que se distingue pelo culto
do estilo, pela pureza da forma e da linguagem e pela simplicidade como resultado do
lavor.
Poeta épico – Ao lado do poeta lírico, há em
Bilac um poeta de tonalidade épica, de que
é expressão o poema O Caçador de Esmeraldas, celebrando os feitos, a desilusão e a
morte do bandeirante Fernão Dias Pais Leme.
Príncipe dos poetas – Bilac é, no seu tempo,
um dos poetas brasileiros mais populares e
mais lidos, tendo sido eleito o “Príncipe dos
Poetas Brasileiros”, no concurso da revista
Fon-Fon (1913).
Hino à Bandeira – Na linha patriótica, compõe a letra do Hino à Bandeira.
OBRAS
1.
2.
3.
4.
Poesias (poesias, 1888)
Crônicas e Novelas (prosa, 1894)
Sagres (poesias, 1898)
Poesias Infantis (poesias, 1904)
Poemas famosos:
1. Ouvir Estrelas
2. Profissão de Fé
3. Língua Portuguesa
Língua Portuguea
Última flor do Lácio, inculta e bela,
És, a um tempo, esplendor e sepultura:
Ouro nativo, que na ganga impura
A bruta mina entre os cascalhos vela...
Amo-te assim, desconhecida e obscura.
Tuba de alto clangor, lira singela,
Que tens o trom e o silvo da procela,
E o arrolo da saudade e da ternura!
Amo o teu viço agreste e o teu aroma
De virgens selvas e de oceano largo!
Amo-te, ó rude e doloroso idioma,
em que da voz materna ouvi: “meu filho!”,
E em que Camões chorou, no exílio amargo,
O gênio sem ventura e o amor sem brilho!
VICENTE DE CARVALHO
Nascimento e morte – Vicente Augusto de
Carvalho nasce em Santos (SP), em 5 de
abril de 1866. Falece em São Paulo (SP), em
22 de abril de 1924.
Direito – Em 1882, aos 16 anos, ingressa na
Faculdade de Direito, bacharelando-se aos
21 anos incompletos.
Faz parte da chamada Boêmia Abolicionista,
cujas reuniões muitas vezes se realizam nos
bancos das praças públicas, impedidos que
são pelas autoridades policiais de irem à sede.
Estréia – Em 1885, publica seu primeiro livro
de versos, Ardêntias, nome inspirado na fosforescência das ondas. A obra faz sucesso,
consagrando-o aos 19 anos.
Muitas atividades – Em Santos, assume a
chefia da imprensa republicana, militando em
todos os jornais. Depois de casado, vira político, fazendeiro, empresário, mas faz carreira
de verdade na área jornalística. Colabora, durante muitos anos, em O Estado de S. Paulo,
em A Tribuna, e funda, em 1905, O Jornal.
Sucesso literário – Publica, em 1908, o livro
Poemas e Canções, com enorme sucesso.
Apelido – Pela obsessão que tinha de falar
do mar, ganha o apelido de “Poeta do Mar”.
OBRAS
1.
2.
3.
4.
Ardêntias (poesias, 1885)
Relicário (pesias, 1888)
Rosa, rosa de amor (poesias, 1901).
Poemas e canções (poesias, 1908).
Poemas famosos:
1.
2.
3.
4.
Velho Tema
Palavras ao Mar
Pequenino Morto (elegia)
A Flor e a Fonte
FRANCISCA JÚLIA
Nascimento e morte – Francisca Júlia nasce
em Xiririca, hoje Eldorado (SP), em 1871. Morre em São Paulo (SP), em 1920.
ESTRÉIA – Em 1895, publico sua primeira
obra, Mármores, um livro de sonetos que causa sensação nas rodas culturais de São Paulo
e do Rio de Janeiro. Olavo Bilac faz-lhe elogios emocionados.
Talento feminino – Num universo inteiramente dominado por poetas do chamado sexo
forte, Francisca Júlia prova que mulher também sabe fazer poesia de qualidade. Cria versos perfeitos, elevando-se ao nivel da “trindade parnasiana” (Olavo Bilac, Raimundo Correia e Alberto de Oliveira), que são seus admiradores e principais incentivadores.
Última obra – Seu segundo e último livro de
poesias, Esfinges, só vem a lume em 1903,
merecendo os mesmos aplausos do primeiro.
OBRAS
1. Mármores (poesias, 1895)
2. Esfinges (poesias, 1903)
Poemas famosos:
1. Musa Impassível
2. Esfinges
Leitura
obrigatória
As Pombas
Raimundo Correia
Vai-se a primeira pomba despertada...
Vai-se outra mais... mais outra... enfim
[dezenas
De pombas vão-se dos pombais, apenas
Raia sanguínea e fresca a madrugada...
E à tarde, quando a rígida nortada
Sopra, aos pombais de novo elas, serenas,
Ruflando as asas, sacudindo as penas,
Voltam todas em bando e em revoada...
Também dos corações onde abotoam,
Os sonhos, um por um, céleres voam,
Como voam as pombas dos pombais;
No azul da adolescência as asas soltam,
Fogem... Mas aos pombais as pombas
[voltam,
E eles aos corações não voltam mais...
1. ENJAMBEMENT – Processo poético de pôr
no verso seguinte uma ou mais palavras que
completam o sentido do verso anterior. O termo francês pode ser substituído por cavalgamento ou encadeamento. No poema As
Pombas, o processo em questão ocorre entre os versos 2/3 e 5/6
2. VERSOS DECASSÍLABOS – Todos os versos do soneto têm dez sílabas métricas.
Vamos verificar o 13.o verso:
Fo/gem/... Mas/ aos/ pom/bais/ as/
1 2
3
4
5
6
7
pom/bas/ vol/tam
8
9 10
3. RIMAS MASCULINAS – São masculinas as
rimas que ocorrem entre palavras oxítonas
ou monossílabas. Em todo o soneto, há
apenas uma rima masculina:
pombais/mais.
4. RIMAS RICAS – Ocorrem entre palavras de
classes diferentes. Encontramo-las nos seguintes pares de versos: 1/4 (despertada:
adjetivo; madrugada: substantivo), 2/3 (dezenas: numeral; apenas: advérbio), 6/7
(serenas: adjetivo; penas: substantivo) e
11/14 (pombais: substantivo; mais: advérbio).
5. SÍMILE – É figura que consiste em comparar, de maneira comum, coisas semelhantes.
Note a comparação que o poeta faz entre o
fenômeno que ocorre com as pombas
(saem dos pombais, mas voltam) e o que
ocorre no coração dos seres humanos (os
sonhos saem e não voltam mais).
Encarte referente ao curso pré-vestibular
Aprovar da Universidade do Estado do
Amazonas. Não pode ser vendido.
Confira as escolas onde será rea
lizado o Simuladão do Aprovar UEA
:
Governador
Eduardo Braga
Vice-Governador
Omar Aziz
Reitor
Lourenço dos Santos Pereira Braga
Vice-Reitor
Carlos Eduardo Gonçalves
Pró-Reitor de Planejamento e Administração
Antônio Dias Couto
Pró-Reitor de Extensão e
Assuntos Comunitários
Ademar R. M. Teixeira
Pró-Reitor de Pós-Graduação e Pesquisa
Walmir Albuquerque
Coordenadora Geral
Munira Zacarias Rocha
Coordenador de Professores
João Batista Gomes
Coordenador de Ensino
Carlos Jennings
Coordenadora de Comunicação
Liliane Maia
Coordenador de Logística e Distribuição
Raymundo Wanderley Lasmar
Produção
Renato Moraes
Projeto Gráfico – Jobast
Alberto Ribeiro
Antônio Carlos
Aurelino Bentes
Heimar de Oliveira
Mateus Borja
Paulo Alexandre
Rafael Degelo
Tony Otani
DESAFIO MATEMÁTI
CO (p. 3)
01. A; 02. B; 03. C; 04.
D; 05. D;
06. B; 07. C; 08. D;
DESAFIO MATEMÁTI
CO (p. 4)
01. B; 02. E; 03. E; 04.
B; 05. E;
06. A;
DESAFIO MATEMÁTI
CO (p. 5)
01. C; 02. C; 03. E; 04.
C; 05. E;
06. A;
DESAFIO FÍSICO (p.
6)
01. III;
02. a) I – aumenta, II
– diminui;
b) A distribuição de
cargas
esfera cria um novo camna
po
elétrico
03. E;
EXERCÍCIOS (p. 7)
01. E; 02. D;
DESAFIO FÍSICO (p.
7)
01. a) errada, b)certa
, c)errada, d)
errada e e)errada;
02. a) Q/3, b) FAC=0
;
03. B;
DESAFIO FÍSICO (p.
8)
01. P = 1,2 . 10-2N;
02. A;
03. a) “Saindo da par
tíicula;
2.105N/C,
b) “Chegando” à partícu
la;
5.104N/C;
04. E;
Editoração Eletrônica
DESAFIO FÍSICO (p.
9)
01. 85V; 02. D; 03. E
DESAFIO LITERÁRIO
(p. 10)
01. D; 02. D; 03. D; 04.
C; 05. E;
Horácio Martins
Este material didático, que será distribuído nos Postos de Atendimento (PAC) na capital e Escolas da Rede Estadual de Ensino, é
base para as aulas transmitidas diariamente (horário de Manaus), de segunda a sábado, nos seguintes meios de comunicação:
• TV Cultura (7h às 7h30); sábados: reprise às 23h
• Amazon Sat (21h30 às 22h)
• RBN (13h às 13h30) reprise: 5h30 e 7h (satélite)
• Rádio Rio Mar (19h às 19h30)
• Rádio Seis Irmãos do São Raimundo
(8h às 9h e reprise de 16h às 16h30)
• Rádio Panorama de Itacoatiara (11h às 11h30)
• Rádio Difusora de Itacoatiara (8h às 8h30)
• Rádio Comunitária Pedra Pintada de Itacoatiara
(10h às 10h30)
• Rádio Santo Antônio de Borba (18h30 às 19h)
• Rádio Estação Rural de Tefé (19h às 19h30) – horário local
• Rádio Independência de Maués (6h às 6h30)
• Rádio Cultura (6h às 6h30 e reprise de 12h às 12h30)
• Centros e Núcleos da UEA (12h às 12h30)
Postos de distribuição:
•
•
•
•
PAC São José – Alameda Cosme Ferreira – Shopping São José
PAC Cidade Nova – Rua Noel Nutles, 1350 – Cidade Nova I
PAC Compensa – Av. Brasil, 1325 – Compensa
PAC Porto – Rua Marquês de Santa Cruz, s/n.°
armazém 10 do Porto de Manaus – Centro
• PAC Alvorada – Rua desembargador João
Machado, 4922 – Planalto
• PAC Educandos – Av. Beira Mar, s/nº – Educandos
www.uea.edu.br e www.linguativa.com.br
Endereço para correspondência: Projeto Aprovar - Reitoria da UEA - Av. Djalma Batista,
3578 - Flores. CEP 69050-010. Manaus-AM