lançamento oblíquo - Cursinho PET

VISUALIZANDO A
INDEPENDÊNCIA DOS
MOVIMENTOS
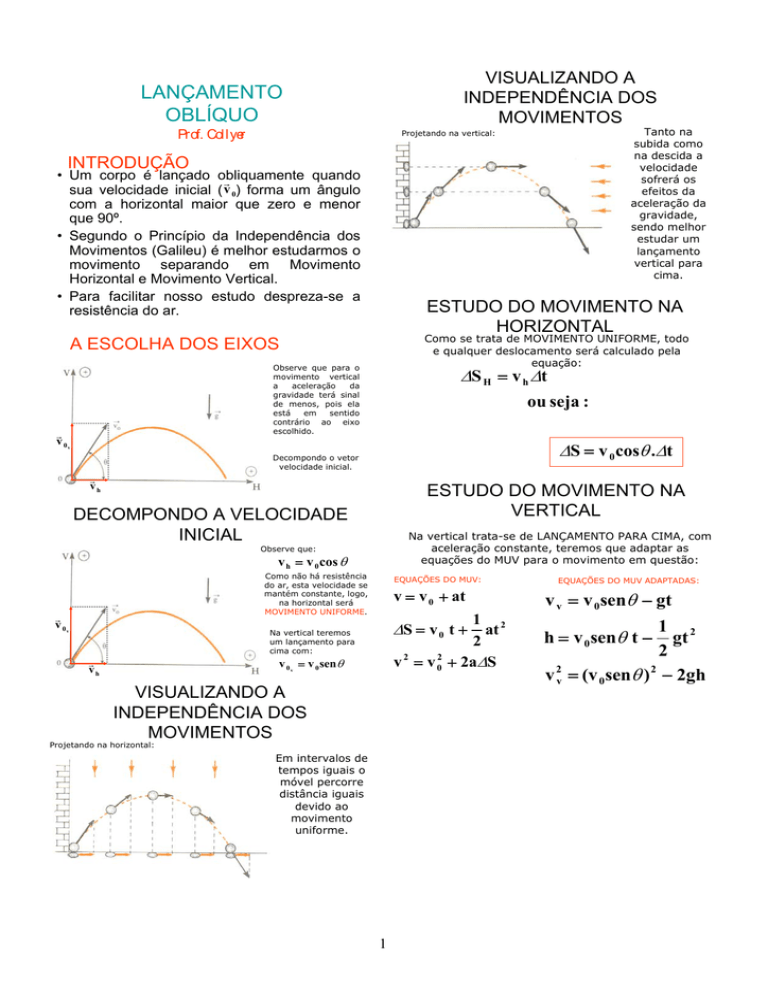
LANÇAMENTO
OBLÍQUO
Tanto na
subida como
na descida a
velocidade
sofrerá os
efeitos da
aceleração da
gravidade,
sendo melhor
estudar um
lançamento
vertical para
cima.
Projetando na vertical:
Prof. Collyer
INTRODUÇÃO
• Um corpo é lançado obliquamente
quando
r
sua velocidade inicial ( v 0) forma um ângulo
com a horizontal maior que zero e menor
que 90º.
• Segundo o Princípio da Independência dos
Movimentos (Galileu) é melhor estudarmos o
movimento separando em Movimento
Horizontal e Movimento Vertical.
• Para facilitar nosso estudo despreza-se a
resistência do ar.
ESTUDO DO MOVIMENTO NA
HORIZONTAL
Como se trata de MOVIMENTO UNIFORME, todo
e qualquer deslocamento será calculado pela
equação:
A ESCOLHA DOS EIXOS
Observe que para o
movimento vertical
a
aceleração
da
gravidade terá sinal
de menos, pois ela
está
em
sentido
contrário ao eixo
escolhido.
r
v 0v
ΔS H = v h Δt
ou seja :
ΔS = v 0 cosθ .Δt
Decompondo o vetor
velocidade inicial.
r
vh
ESTUDO DO MOVIMENTO NA
VERTICAL
DECOMPONDO A VELOCIDADE
INICIAL
Na vertical trata-se de LANÇAMENTO PARA CIMA, com
aceleração constante, teremos que adaptar as
equações do MUV para o movimento em questão:
Observe que:
v = v cos θ
h
0
Como não há resistência
do ar, esta velocidade se
mantém constante, logo,
na horizontal será
MOVIMENTO UNIFORME.
r
v 0v
EQUAÇÕES DO MUV:
v 0 v = v 0 senθ
r
vh
v = v 0 + at
v v = v 0 senθ − gt
1 2
at
2
v 2 = v 02 + 2aΔS
h = v 0 senθ t −
ΔS = v 0 t +
Na vertical teremos
um lançamento para
cima com:
VISUALIZANDO A
INDEPENDÊNCIA DOS
MOVIMENTOS
Projetando na horizontal:
Em intervalos de
tempos iguais o
móvel percorre
distância iguais
devido ao
movimento
uniforme.
1
EQUAÇÕES DO MUV ADAPTADAS:
1 2
gt
2
v 2v = (v 0 senθ ) 2 − 2gh
UMA PERGUNTA
ESTUDO DO MOVIMENTO NA
VERTICAL
• v0 é uma característica da arma.
• g é uma característica do planeta.
• Não podem ser mudados.
• Quando é que o alcance de uma arma será
máximo?
Se aplicarmos alguns conhecimentos às equações do
movimento na vertical, poderemos deduzir fórmulas
especiais, as quais não aconselho decorar “e sim
fazer a dedução”:
Você obterá:
Cálculo do tempo de subida:
Como no ponto de altura
máxima a velocidade vertical
é nula, faça vv = 0 na
equação v v = v 0 senθ − gt
h = v 0 senθ t −
1 2
gt
2
v v = v 0 senθ − gt
v 2 .sen 2θ
A= 0
g
0 = v 0 senθ − gt
gt = v 0 senθ
t sub =
v 0 senθ
g
Observe que:
v o2 .2senθ cosθ
A=
g
0 = v 0 senθ − gt
v 0 senθ
g
⇒
t total = 2.
v 0 senθ
g
ESTUDO DO MOVIMENTO NA
VERTICAL
Cálculo da altura máxima atingida:
Como no ponto de altura máxima temos v v = 0 :
v 2v = (v 0 senθ ) 2 - 2gh
0 = (v 0 senθ ) 2 - 2gh
2gh = (v 0 senθ ) 2
h max =
(v 0 senθ ) 2
2g
CÁLCULO DO ALCANCE
Alcance (A) é a distância que o
projétil atinge.
ΔSH = v 0 cosθ .Δt mas Δt TOT = 2.
log o : A = v 0 cosθ 2.
2.v 0senθ
g
Como o alcance é
uma distância na
horizontal, ela
deve ser
calculada pela
equação do
movimento na
horizontal:
2.v 0senθ v o2 .2senθ cosθ
=
g
g
A=
2θ = 900
θ = 450
• Quando é que, mudando os ângulos de
lançamentos, atingiremos sempre o mesmo
alcance?
Como no lançamento para cima aprendemos
que tsubida= tdescida, o tempo total do
= v 0 senθ − gtserá igual a duas vezes o t
v vmovimento
subida.
t sub =
Ou seja:
A ÚLTIMA PERGUNTA
ESTUDO DO MOVIMENTO NA
VERTICAL
Você
obterá:
= v 0 sen
gt
θ
A será máximo,
quando sen2θ for
máximo.
v 02 .sen 2θ
g
2
Toda vez que tivermos
ângulos
complementares, o
produto 2senθcosθ,
apresentará o mesmo
valor, logo o projétil
terá o mesmo alcance.