Deslocamento, velocidade e aceleração linear e

Deslocamento, velocidade
e aceleração linear e
angular
Definição
Para estudar o movimento dos objetos utilizamos conceitos como
espaço s, velocidade v e aceleração a.
Definição
Para movimento circular existe também
Aceleração centrípeta
Período de revolução
Equação horária do
movimento
Definição
Equação horária da velocidade
Equação horária da posição
Equação de Torricelli
Definição
Equações lineares e angulares
Equação linear
Equação angular
Definição
Relações entre grandezas lineares e angulares
s = θR
θ em rad
vtan = ωR ω em rad/s
atan= αR α em rad/s2
Definição
Movimento combinado de translação e rotação
Translação
Velocidade do centro
de massa vcm
Rotação em torno do
centro de massa:
Para rolamento sem
deslizamento, todos os
pontos da periferia se
movem com velocidade
escalar vcm
Movimento combinado de
rotação e translação,
rolamento sem deslizamento.
A roda fica instantaneamente
em repouso quando toca no
solo.
Exemplo
Exemplo
Alysson arremessa seu IPhone para o alto
a uma velocidade inicial de 12m/s. Em
quanto tempo seu IPhone atinge a altura
máxima? Qual sua altura máxima?
Exemplo
Alysson arremessa seu IPhone para o alto
a uma velocidade inicial de 12m/s. Em
quanto tempo seu IPhone atinge a altura
máxima? Qual sua altura máxima?
V0 = 12 m/s
g = 9,8 m/s2
x=?
Exemplo
Solução:
Exemplo
Exemplo
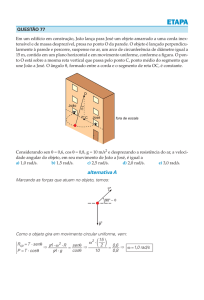
Engenheiro mecânico Jr Metrô-SP 2012
Um perito concluiu que um trem trafegava com velocidade constante
quando acionou os freios, percorrendo uma distância de 25 m até a
parada total, próximo a uma estação de passageiros. Assumindo que
a frenagem ocorreu a uma taxa constante de 2 m/s2, a velocidade
com que o trem trafegava é igual a
(A) 36 km/h
(B) 48 km/h
(C) 60 km/h
(D) 68 km/h
(E) 80 km/h
Exemplo
Dados:
Aceleração constante a = -2 m/s2, vfinal=0, deslocamento 25 m.
Solução:
0 = vo2 - 2.2.25
Vo=10 m/s
Vo=36 km/h
alternativa A
Exemplo
Engenheiro mecânico Jr Metrô-SP 2012
Uma roda rígida de um veículo, de raio 100 mm, rola sem escorregar
sobre um plano com rotação constante de 300 rpm. As velocidades do
veículo e do ponto de contato da roda com o plano são,
(A)
(B)
(C)
(D)
(E)
30 m/s e 3,14 m/s, respectivamente.
3,14 m/s e nula, respectivamente.
ambas iguais a 3,14 m/s.
ambas iguais a 30 m/s.
ambas nulas.
Exemplo
Solução:
rotação sem escorregar → velocidade no ponto de contato roda/solo = 0
Alternativa B
Velocidade do veículo = vcm
Velocidade tangencial vtan= ωR
rotação sem escorregar vtan= vcm
R = 0,1 m e ω = 300 rpm = 300.2π/60 = 10 π rad/s
vcm= ωR
Então vcm= π m/s
Exemplo
Exemplo
[Geofísico jr Petrobras 2005]
Exemplo
movimento vertical:
y = vo.senθ.t – g.t2/2
v = vo.senθ – gt
vy2 = (vo.senθ)2 – 2g y
(1)
(2)
(3)
altura máxima: y = h → vy = 0
de (5) e considerando mesmo h
(vo1.senα)2/2g = (vo2.senβ)2/2g
(vo1.senα) = (vo2.senβ)
então de (4)
de (2)
t = vo.senθ/g
(4)
t1 = t2
alternativa A
de (3)
h = (vo.senθ)2/2g
(5)