FÍSICA

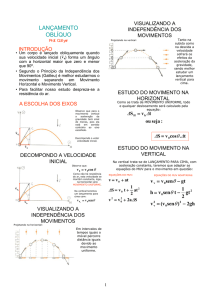
FÍSICA
Questão 01
A figura abaixo ilustra um pequeno bloco e uma mola sobre uma mesa retangular de largura d, vista de cima. A mesa é
constituída por dois materiais diferentes, um sem atrito e o outro com coeficiente de atrito cinético μ igual a 0,5. A mola tem uma
de suas extremidades fixada no ponto A e a outra no bloco. A mola está inicialmente comprimida de 4 cm, sendo liberada para
que o bloco oscile na região sem atrito na direção y. Depois de várias oscilações, ao passar pela posição na qual tem máxima
velocidade, o bloco é atingido por uma bolinha que se move com velocidade 2 m/s na
direção x e se aloja nele. O sistema é imediatamente liberado da mola e se desloca na
parte áspera da mesa. Determine:
a) o vetor quantidade de movimento do sistema bloco + bolinha no instante em que ele é
liberado da mola;
b) a menor largura e o menor comprimento da mesa para que o sistema pare antes de
cair.
Dados: comprimento da mola = 25 cm;
Constante elástica da mola = 10 N/cm;
Massa da bolinha = 0,2 kg;
Massa do bloco = 0,4 kg;
Aceleração da gravidade = 10 m/s2.
Resolução:
a) Cálculo da máxima velocidade do bloco:
kx 2 mv 2
=
2
2
v = x⋅
k
10 ⋅102
m/s
= 4 ⋅10−2 ⋅
m
0, 4
v = 4 ⋅10−2 ⋅10 ⋅ 5 m / s
v = 2 m/ s
Cálculo da quantidade de movimento do sistema bloco + bolinha imediatamente antes da colisão:
Q2 = m2 v2 = 0, 2 kg ⋅ 2 m / s = 0, 4 kg m / s
Q1 = m1v1 = 0, 4 ⋅ 2 kg m / s = 0,8 kg m / s
Q
2
2
Qantes
= Q12 + Q22 = 0,82 + 0, 42
∴ QAntes = 0, 4 ⋅ 5 kg m / s
Q
Antes
Q
1
Na colisão temos conservação da quantidade de movimento,
JG
JG
logo: Q depois = Q antes
x
q
Qdepois = 0,89 kg m / s e θ = arc tg 2
Qdepois
y
b) Durante o percurso da parte com atrito temos:
C
A
q
τ Fat = ΔEc
Fat ⋅ AB ⋅ cos 180º =
V
A
−μmg ⋅ AB = −
mv B2 mv A2
−
2
2
mv A2
2
⎛ Qdepois ⎞
⎜
⎟
2
vA ⎝ m ⎠
AB =
=
2μg
2 ⋅μ ⋅ g
B
2
2
⎛ 0, 4 5 ⎞
⎜⎜
⎟
0, 6 ⎟⎠
AB = ⎝
2 ⋅ 0,5 ⋅10
2
∴ AB = m
9
Lembrando que tg θ = 2 temos BC = 2 ⋅ AC.
AB 2 = BC 2 + AC 2
4
= 4 AC 2 + AC 2
81
4
AC 2 =
81.5
∴ AC = 0,10 m e BC = 0, 20 m
Do exposto concluímos que a menor largura d e o menor comprimento L da mesa para que o conjunto não caia serão dados
por:
d
= AC ⇒ d = 0, 20 m
2
L = BC + 0, 25
↑
comprimento original
da mola
L = 0, 45 m
2
Questão 02
Em um recipiente, hermeticamente fechado por uma tampa de massa M, com volume
interno na forma de um cubo de lado a, encontram-se n mols de um gás ideal a uma
temperatura absoluta T. A tampa está presa a uma massa m por um fio que passa por uma
roldana, ambos ideais. A massa m encontra-se na iminência de subir um plano inclinado de
ângulo θ com a horizontal e coeficiente de atrito estático μ. considerando que as variáveis
estejam no Sistema Internacional e que não exista atrito entre a tampa M e as paredes do
recipiente, determine m em função das demais variáveis.
Dados: aceleração da gravidade = g;
Constante universal dos gases perfeitos = R.
Resolução:
Considerando a pressão atmosférica na região como sendo P0 temos:
Equilíbrio do êmbolo
∑F
=0
T’ + FG = F0 + P’
T’ + P · A = P0 ·A + Mg ⇒ T’ + P · a2 = P0 · a2 + Mg (1)
Equilíbrio do bloco:
∑F = 0
N = P” · cosθ
N = mg cosθ
T’ = P” senθ + Fate
T’ = mg senθ +μe · N
∴ T’ = mg senθ + μe · mg · cosθ
T’ = mg (senθ + μe cosθ) (2)
Para o gás ideal podemos escrever:
P · V = nRT
P · a3 = nRT
nRT
P = 3 (3)
a
De (1), (2) e (3) vem:
nRT
mg (senθ + μe cosθ) + 3 · a2 = P0 · a2 + M · g
a
mg (senθ + μe cosθ) = P0 · a2 + Mg –
∴m=
nRT
a
⎛ P ·a 2
nRT ⎞
·⎜ 0
+M –
⎟
g ·a ⎠
( senθ + μe cos θ ) ⎝ g
1
Se fosse vácuo do lado de fora do recipiente, bastaria fazermos P0 = 0 na equação acima que ficaríamos com
nRT
1
m=
· (M –
).
ga
( senθ + μe cos θ )
3
Questão 03
Uma máquina opera a 6000 ciclos termodinâmicos por minuto, executando o ciclo de Carnot, mostrado na figura abaixo. O
trabalho desta máquina térmica é utilizado para elevar verticalmente uma carga de 1000 kg com velocidade constante de 10 m/s.
Determine a variação da entropia no processo AB, representado na figura. Considere a aceleração da gravidade igual a 10 m/s2
e os processos termodinâmicos reversíveis.
Temperatura
600K
B
A
300K
Entropia
Resolução:
i) Cálculo da potência útil:
mg Δ h
m
m
Pútil =
= mgv = 1000 kg · 10 2 · 10
Δt
s
s
Pútil = 1,0 · 105 W
ii) Cálculo do rendimento:
T
1
300
η=1– 1 =1–
= = 50 %
600
T2
2
De i e ii temos:
P
Pretirada da fonte quente = útil = 2,0 ⋅105 W
η
6000 Qretirado da fonte quente em um ciclo
60s
Qretirado da
fonte quente em um ciclo
J
s
= 2, 0 ⋅103 J
= 2,0 ⋅105
Daí temos:
Δ HAB =
Qretirado da fonte quente em um ciclo
T fonte quente
2 , 0 · 103 J
600 K
Δ HAB = 3,3 J/K
Δ HAB =
Questão 04
A malha de resistores apresentada na figura a seguir é conectada pelos terminais A e C a uma fonte de tensão constante. A
malha é submersa em um recipiente com água e, após 20 minutos, observa-se que o líquido entra em ebulição. Repetindo as
condições mencionadas, determine o tempo que a água levaria para entrar em ebulição, caso a fonte tivesse sido conectada aos
terminais A e B .
4
Resolução:
Se uma d.d.p. U é aplicada nos terminais A e C , podemos encontrar RAC :
VB = VE = VD
RAC =
Primeira forma de calcular RAB :
Usando que:
equivale a:
5
2
R
3
Temos
1
1
1
1
8
= +
+
⇒ RAB = R
15
RAB R 2 R ⎛ 8 R ⎞
⎜
⎟
⎝ 3 ⎠
Segunda forma de calcular RAB :
⇒
1
1
1
=
+
RAB ⎛ 2 R ⎞ ⎛ 8R ⎞
⎜
⎟ ⎜
⎟
⎝ 3 ⎠ ⎝ 3 ⎠
8
RAB = R
15
Considerando P =
Q
, com Q de mesmo valor em ambas situações, temos:
Δt
Q1 = Q2
P1 ⋅ Δt1 = P2 ⋅ Δt2
U12
R1
⋅ Δt1 =
U 22
R2
⇒
Mas U1 = U 2 , então:
⋅ Δt 2
Δt1 =
R1
⋅ Δt 2
R2
Δt AB
8
R
RAB
=
⋅ Δt AC ⇒ Δt AB = 15 ⋅ 20 ⇒ Δt AB = 16 min
2
RAC
R
3
6
Questão 05
A figura abaixo mostra uma caixa d’água vazia, com peso de 125 kgf , sustentada por um cabo inextensível e de massa
desprezível, fixado nos pontos A e D . A partir de um certo instante, a caixa d’água começa a ser enchida com uma vazão
constante de 500 L / h . A roldana B possui atrito desprezível. Sabendo que o cabo possui seção transversal circular de 1 cm de
diâmetro e que admite força de tração por unidade de área de no máximo 750 kfg / cm 2 , determine o tempo de entrada de água
na caixa, em minutos, até que o cabo se rompa.
Dado: peso específico da água = 1000 kfg / cm3
π ≅ 3,14
B
D
2,5 m
C
caixa
d'água
5,5 m
A
6,0 m
6,0 m
2,5 m
Resolução:
Obs.: Para a resolução desta questão, consideraremos os pontos B e D alinhados horizontalmente.
JJG
Tensão de Ruptura TR
( )
Área da seção transversal do cabo ( Ac )
Ac =
π D2
=
4
750 kgf
3,14 ⋅12
= 0,785 cm 2
4
1 cm 2
0, 785 cm 2
TR
TR = 588, 75 kgf
JJG
Peso de água PA
( )
B
y
2,5m
T1
2,5m
T1x
T1y
6m
T2y
45°
q
T3
T2x
D
T2
2,5m
x
T3
Obs.:
PA PR
d 2 = 6 2 + 2 , 52 ⇒ d = 6 , 5 m
2 ,5
5
senθ =
⇒ senθ =
6 ,5
13
6
12
cosθ =
⇒ cosθ =
6 ,5
13
7
FRx = 0 ⇒ T1x = T2 x
T1 ⋅ cos45º = T2 ⋅ cosθ
2
12
= T2 ⋅
2
13
12 2
T1 =
T2
13
Como T1 > T2 , teremos: T1 = TR = 588, 75 kgf
T1 ⋅
Fazendo
2 = 1, 41 , teremos:
12 2
T2
13
12 ⋅1, 41
588, 75 =
T2
13
T2 = 452 ,35 kgf
T1 =
FRy = 0 ⇒ T1 y + T2 y = T3
Como T3 = PA + PR , onde PR = 125 kgf (peso do recipiente), teremos:
T1 y + T2 y = PA + PR
T1 ⋅ sen45º +T2 ⋅ senθ = PA + 125
2
5
+ 452 ,34 ⋅ = PA + 125
2
13
PA = 464 ,05 kgf
588, 75 ⋅
Tempo de entrada de água ( Δt )
ρA =
PA
464 , 05
⇒ 1000 =
V
V
V = 0 , 46405 m3 = 464 , 05 L
V
464 , 05
⇒ 500 =
Δt
Δt
Δt = 0 ,9281 h
Z=
Δt = 55, 7 min
Questão 06
Em certa experiência, ilustrada na figura abaixo, uma fina barra de latão, de comprimento L = 8 m , inicialmente à temperatura de
20ºC , encontra-se fixada pelo ponto médio a um suporte presa à superfície e pelas extremidades e dois cubos idênticos A e B ,
feitos de material isolante térmico e elétrico. A face esquerda do cubo A está coberta por uma fina placa metálica quadrada P1 ,
distante d0 = 5 cm de uma placa idêntica P2 fixa, formando um capacitor de 12 μ F , carregado com 9 μ F . Na face direita do cubo
B está fixado um espelho côncavo distante 11 cm de um objeto O , cuja imagem I está invertida. Aquece-se a barra até a
temperatura T em ºC , quando então a distancia entre O e I se torna igual a 24 cm e a imagem I , ainda invertida, fica com
quatro vezes o tamanho do objeto O .
Considerando a superfície sob os cubos sem atrito, determine:
a) a distância focal do espelho;
b) a tensão elétrica entre as placas ao ser atingida a temperatura T ;
c) a temperatura T .
Dados: coeficiente de dilatação linear do latão (α ) = 1,8 × 10−5 ( ºC )−1 .
8
Resolução:
Na situação final a distância entre objeto e imagem é de 24 cm e o aumento linear transversal vale A = – 4:
− pÍf
pIf − pOf = 24 e A = –4 =
, logo:
pOf
(
)
4 pOf = 24 + pOf ⇒ pOf = 8cm e pIf = 32 cm
Por fim:
1
1
1
1 1 5
=
+
=
+ =
⇒ p = 6, 4 cm
f
pIf pOf 32 8 32
b) Pela figura nota-se:
ΔL = pO − pOf = 11 − 8 = 3 cm
Assim, no capacitor:
d = do − ΔL = 5 − 3 = 2 cm
εA
∴ εA = CO ⋅ do
do
Que usado na situação final:
εA CO ⋅ do
F ⋅ 5 cm
C=
=
= 12μ
= 30μF
d
d
2 cm
E ainda, CO =
E por fim: U =
Q 9μC
=
= 0,3V
C 30μF
c) Podemos calcular a dilatação da barra da forma:
ΔL
3 cm
=
= 417º C
L ⋅ α 4 ⋅102 cm ⋅1,8 ⋅10-5 º C −1
E assim: T = 20º +ΔT = 437º C
ΔL = L ⋅ α ⋅ ΔT ∴ ΔT =
Questão 07
Considere uma pequena bola de gelo de massa M suspensa por um fio de densidade linear de massa p e comprimento L à
temperatura ambiente. Logo abaixo deste fio, há um copo de altura H e diâmetro D boiando na água. Inicialmente o copo está
em equilíbrio com um comprimento C submerso. Este fio é mantido vibrando em sua freqüência natural à medida que a bola de
gelo derrete e a água cai no copo. Determine a freqüência de vibração do fio quando o empuxo for máximo, ou seja, quando o
copo perder a sua flutuabilidade.
Dados: aceleração da gravidade = g;
massa específica da água = μ
Resolução:
O empuxo adicional corresponderá ao peso do volume V do copo que passará a ficar submerso:
ΔE = PA = μ ⋅ V ⋅ g
PA = μ ⋅
PA =
πD 2
⋅h⋅g
4
μg πD 2
⋅(H − C)
4
Mas, o peso acional PA é o mesmo perdido pela bola de gelo:
P ' gelo = PO − PA
P0= M·g
P 'gelo = M ⋅ g −
h
C
D
H
μ · g π· D2
(H − C)
4
P 'gelo = f( tração no
fio )
9
F = Mg −
μ · g π· D2
(H − C)
4
A freqüência natural de vibração será dada por:
f1 =
1 F
2L ρ
f1 =
⎤
μ · π· D2
1
1⎡
⋅
⋅ g ⋅ ( H – C )⎥
⎢ Mg –
2 L ρ ⎣⎢
4
⎦⎥
f1 =
1 g⎡
4 ⋅ M – μ⋅π⋅ D 2 ⋅ ( H – C ) ⎤
⎦
4L ρ ⎣
Questão 08
O circuito ilustrado na figura abaixo apresenta um dispositivo F capaz de gerar uma corrente contínua e constante I,
independentemente dos valores da resistência R e da capacitância C. Este circuito encontra-se sujeito a variações na temperatura
ambiente Δθ. O calor dilata apenas as áreas Ac das placas do capacitor e AR da seção reta do resistor. Considere que não variem
com a temperatura a distância d entre as placas do capacitor, a permissividade e do seu dielétrico, o comprimento L do resistor e
sua resistividade p. Determine a relação entre os coeficientes de dilatação superficial βc das placas do capacitor e βR da seção
reta do resistor, para que a energia armazenada pelo capacitor permaneça constante e independente da variação da temperatura
Δθ. Despreze o efeito Joule no resistor e adote no desenvolvimento da questão que (βR Δθ)2 << 1.
Resolução:
A energia armazenada no capacitor pode ser calculada da forma
CU 2
,
2
onde ainda podemos calcular
εA
ρL
⋅I
C = c e U = R⋅I =
d
AR
Assim, levando em conta variações de temperatura Δθ devemos escrever:
A (1 + β c Δθ )
ρ LI
eU=
C =ε⋅ c
d
AR (1 + β R Δθ )
E=
E a nova energia acumulada será:
2
E=
E=
⎞
(1 + β c Δθ ) ⎛
1
ρ LI
⋅ ε ⋅ Ac
⋅ ⎜⎜
⎟⎟ ⇒
d
2
⎝ AR (1 + BR Δθ ) ⎠
ε ⋅ ρ 2 ⋅ L2 I 2 ⋅ Ac ⎛ (1 + β c Δθ ) ⎞
2 ⋅ dAR 2
⎟
⋅⎜
⎜ (1 + β Δθ )2 ⎟
R
⎝
⎠
Sendo assim, para que E não varie, precisamos que o fator seja constante e
1 + β c Δθ
(1 + β R Δθ )
Logo,
2
=
1 + β c Δθ
1 + 2β R Δθ + ( β R Δθ )
2
= 1 , onde podemos desprezar ( β R Δθ )2
1 + β c Δθ
=1
1 + 2 β R ⋅ Δθ
1 + β c ⋅ Δθ = 1 + 2 β R ⋅ Δθ ⇒ β c ⋅ Δθ = 2 β R ⋅ Δθ ⇒
βc
=2
βR
10
1 + β c Δθ
(1 + β R Δθ )2
=1
Questão 09
Uma partícula com, carga elétrica positiva q e massa M apresenta velocidade inicial v na direção y em t = 0, de acordo com a
figura ao lado. A partícula está submetida a um campo magnético variável e periódico, cujas componentes estão mostradas na
figura ao lado em função do tempo. Verifica-se, que durante o primeiro pulso da componente Bz, a partícula realiza uma
trajetória de um quarto de circunferência, enquanto que no primeiro pulso da componente By realiza uma trajetória de meia
circunferência. Determine:
a) o período T em função de M · q e b2.
b) a relação b / b2.
c) o gráfico da componente x da velocidade da partícula em função do tempo durante um período.
B
B
Resolução:
a) Seja Δt o tempo que seria necessário para a partícula realizar uma circunferência completa sob ação de bz caso sua duração
fosse suficientemente grande:
2πM
Δt =
qbz
Do enunciado notamos que
T=
10 Δt 5 2πM
= ⋅
4
2 qbz
T=
5πM
qbz
Δt
= 0,1 T , daí:
4
(I )
b) Seja Δt’ o tempo que seria necessário para a partícula realizar uma circunferência completa sob ação de b caso sua duração
fosse suficientemente grande
2πM
Δt ' =
qb
Δt '
= 0, 05 T , logo:
2
2πM 20πM
T = 10 Δt ' = 10 ⋅
=
( II )
qb
qb
De (I) e (II) vem:
5πM 20πM
b
T=
=
⇒
=4
q bz
qb
bz
c) Primeiro façamos um gráfico da trajetória da partícula:
Agora podemos escrever
z
t0 = 0
x
t7= 0,95 T
t1= 0,2 T
y
t2 = 0,3 T
t6= 0,75 T
t5 = 0,65 T
t3 = 0,45 T
t4 = 0,50 T
11
Do exposto na figura acima, atendo-nos somente à velocidade no eixo x, podemos construir o gráfico abaixo:
Questão 10
Um radar Doppler foi projetado para detectar, simultaneamente, diversos alvos com suas correspondentes velocidades radiais de
aproximação. Para isso, ele emite uma onda eletromagnética, uniformemente distribuída em todas as direções e, em seguida,
capta os ecos refletidos que retornam ao radar.
Num experimento, o radar é deslocado com velocidade constante v em direção a um par de espelhos, conforme ilustra a figura
abaixo. Calcule os vetores de velocidade relativa (módulo e direção) de aproximação dos quatro alvos simulados que serão
detectados pelo radar após as reflexões no conjunto de espelhos, esboçando para cada um dos alvos a trajetória do raio
eletromagnético no processo de detecção.
π
π
Dado: < θ < .
4
3
Resolução:
A velocidade radial de aproximação com que o observador O percebe as imagens I1 e I4 são, em módulo, são iguais a 2 v senθ .
As direções são as das retas OI1 e OI4 indicadas na figura.
I3
I4
I2
I1
v
v
q
q q
q
q
v sen q
v
q
v sen q
Já as imagens I2 e I3 não são percebidas por O. Isso ocorre uma vez que nenhuma onda eletromagnética originada em O retorna
π
a ele após duas reflexões nos espelhos. Para a percepção de I2 e I3 o ângulo θ deveria ser menor que .
4
12
⎤π π
Se o ângulo θ estivesse no intervalo ⎥ ,
⎦5 4
⎡
⎢ , teríamos:
⎣
I3
I2
v
a
v
q
I4
v cos a
90°–q
90°–q
I1
90°–a
va
v cos a
O
As soluções para I1 e I4 são idênticas às já apresentadas.
Da figura notamos que:
90º −θ + 90º −α + 90º −θ = 180º
α = 90º −2θ
cos α = cos ( 90º −2θ ) = sen 2θ = 2sen θ cos θ
Finalmente as velocidades de aproximação de I2 e I3 em relação a O serão, em
2 v cos α = 2 v 2senθ cos θ = 4 v senθ cos θ . Suas direções são dadas pelas retas OI1 e OI2 conforme a figura.
13
módulo,
iguais
a
Professores:
Física
Adriano Medeiros
Bernadelli
Frederico Bittencourt
Marcelo Moraes
Rodrigo Lacerda
Walfredo
Digitação e Diagramação
Antônio A. Vitor
Deise Lara
Plínio Lagares
Val Pinheiro
Vinícius Eduardo
Projeto Gráfico
Antônio A. Vitor
Assistente Editorial
Alicio Roberto
Supervisão Editorial
Alicio Roberto
Rodrigo Bernadelli
Marcelo Moraes
Copyright©Olimpo2007
A Resolução Comentada das provas do IME poderá ser obtida diretamente no
OLIMPO Pré-Vestibular, ou pelo telefone (62) 3251 – 9009
As escolhas que você fez nessa prova, assim como outras escolhas na vida, dependem de conhecimentos, competências,
conhecimentos e habilidades específicos. Esteja preparado.
14
15
8
MATRÍCULAS ABERTAS
TEL.(62) 3251-9009
16