Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 34 – O CAMPO MAGNÉTICO
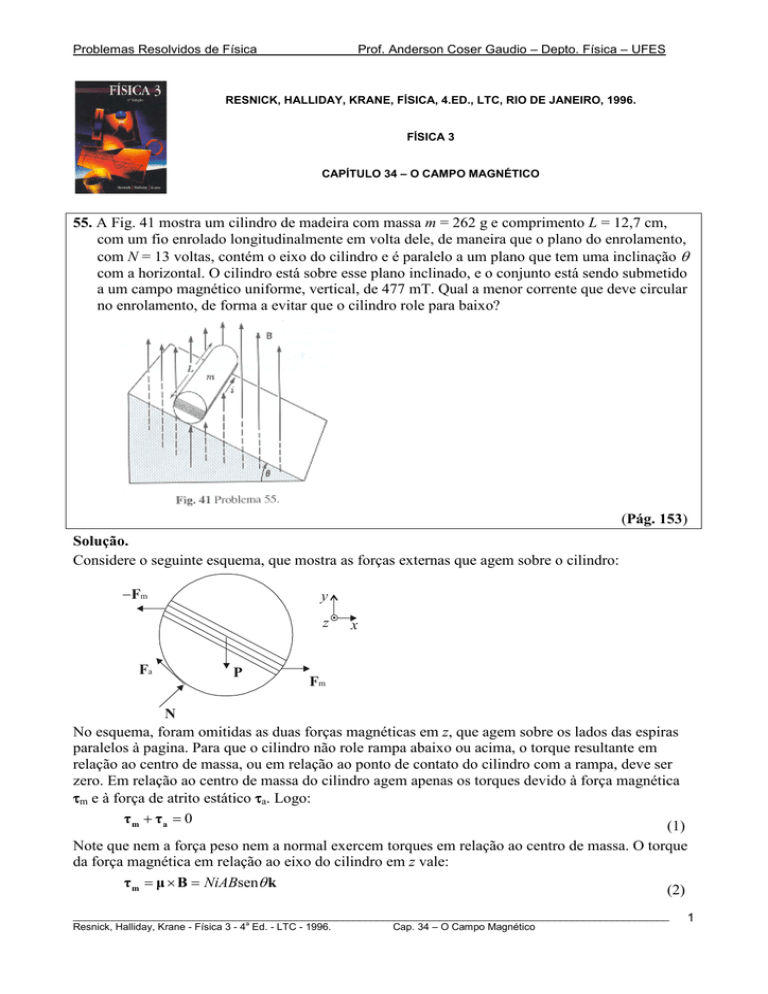
55. A Fig. 41 mostra um cilindro de madeira com massa m = 262 g e comprimento L = 12,7 cm,
com um fio enrolado longitudinalmente em volta dele, de maneira que o plano do enrolamento,
com N = 13 voltas, contém o eixo do cilindro e é paralelo a um plano que tem uma inclinação θ
com a horizontal. O cilindro está sobre esse plano inclinado, e o conjunto está sendo submetido
a um campo magnético uniforme, vertical, de 477 mT. Qual a menor corrente que deve circular
no enrolamento, de forma a evitar que o cilindro role para baixo?
(Pág. 153)
Solução.
Considere o seguinte esquema, que mostra as forças externas que agem sobre o cilindro:
−Fm
y
z
Fa
P
x
Fm
N
No esquema, foram omitidas as duas forças magnéticas em z, que agem sobre os lados das espiras
paralelos à pagina. Para que o cilindro não role rampa abaixo ou acima, o torque resultante em
relação ao centro de massa, ou em relação ao ponto de contato do cilindro com a rampa, deve ser
zero. Em relação ao centro de massa do cilindro agem apenas os torques devido à força magnética
τm e à força de atrito estático τa. Logo:
τm + τa =
0
(1)
Note que nem a força peso nem a normal exercem torques em relação ao centro de massa. O torque
da força magnética em relação ao eixo do cilindro em z vale:
τ m = μ × B = NiABsenθ k
(2)
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 34 – O Campo Magnético
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
O torque da força de atrito em relação ao mesmo eixo é dado por:
τ a= ra × Fa
(3)
O cálculo da força de atrito pode ser feito pelas componentes das forças em x e y. Forças em x:
N x − Fax =
0
Nsenθ − Fa cos θ =
0
N=
Fa cos θ
senθ
(4)
Forças em y:
N y + Fay − P =
0
Ncosθ + Fa senθ =
mg
(5)
Substituindo-se (4) em (5):
Fa cos θ
cosθ + Fa senθ =
mg
senθ
 cos 2 θ + sen 2θ
Fa 
senθ


 = mg

Fa = mgsenθ
(6)
Pode-se agora resolver (3):
τ a = −rmgsenθ k
(7)
Substituindo-se (2) e (7) em (1):
NiAB sen θ k − rmg sen θ k =
0
Ni (2rL) B = rmg
2NiLB = mg
( 0, 262 kg ) ( 9,81 m/s )
mg
=
i =
= 1, 6318 A
2 NLB 2 (13)( 0,127 m )( 0, 477 T )
2
i ≈ 1, 63 A
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 34 – O Campo Magnético
2