ESTABILIDADE DA α–QUIMOTRIPSINA A pH ALCALINO POR

ESTABILIDADE DA α–QUIMOTRIPSINA A pH ALCALINO POR
ABSORÇÃO NO UV
Ana Rita Gafaniz*, Nuno Santos** e Rúben Pereira***
* Nº55763
Mestrado Integrado em Engenharia Biomédica
Instituto Superior Técnico – Departamento de Física
e-mail: [email protected]
** Nº55746
Mestrado Integrado em Engenharia Biomédica
Instituto Superior Técnico – Departamento de Física
e-mail: [email protected]
*** Nº55754
Mestrado Integrado em Engenharia Biomédica
Instituto Superior Técnico – Departamento de Física
e-mail: [email protected]
Palavras-chave: α-Quimotripsina, Espectrofotometria
Desnaturação, Estabilidade Térmica a pH Alcalino
de
Absorção
no
UV,
Resumo Com este trabalho experimental pretendeu-se estudar a estabilidade
térmica da α-quimotripsina a pH alcalino. Para tal, recorreu-se à medição de
absorvância de várias amostras da proteína, a várias temperaturas (no intervalo entre
25ºC e 60ºC), aos comprimentos de onda de 250nm e 278nm. Esta técnica permitiu
seguir o grau de desnaturação da proteína pela observação da alteração do espectro de
absorção do tirosinato (resultante da ionização dos resíduos de tirosina por exposição
ao solvente) no UV.
Após o registo dos valores de absorvância das várias amostras representaram-se
graficamente as fracções de α-quimotripsina desnaturada e a variação de energia livre
em função da temperatura. Calculou-se também a temperatura de transição e os
valores das variações de entalpia e de entropia.
A experiência foi realizada por cada um dos grupos para diferentes valores de pH.
Os resultados obtidos apontam para uma desestabilização térmica da proteína com
o aumento do pH, tendo-se obtido os valores de temperatura de transição de 42,25ºC,
40,81ºC, 40,50ºC e 39,87ºC para os valores de pH de 9,8, 10,2, 10,6 e 11,
respectivamente.
1
1. INTRODUÇÃO TEÓRICA
Este trabalho teve como objectivo, o estudo da estabilidade da α-quimotripsina com
o aumento da temperatura num meio de pH alcalino, com base nas alterações no
espectro de absorção da proteína.
1.1. Determinação da temperatura de transição da proteína
A experiência realizada é feita num meio alcalino, uma vez que a reacção em causa
requer uma ionização do grupo fenol da Tyr, que apenas é mensurável para valores de
pH superiores a 9,0.
O
O
NH2
NH2
OH
pK ~ 10.1
O
-
Figura 1. Ionização do grupo fenol da tirosina.
Quando a proteína está na sua forma nativa, as Tyr encontram-se “escondidas” no
interior da sua estrutura terciária e não são afectadas por variações de pH [1]. Contudo,
à medida que se aumenta a temperatura, dá-se a desnaturação (desenrolamento) da
proteína e o número de resíduos de Tyr em contacto com o meio aumenta. Como é
possível observar na reacção esquematizada na figura 1, ao entrar em contacto com o
meio, o grupo fenol sofre perda do hidrogénio, ocorrendo ionização do grupo OH
(pK≈10,1) formando assim o ião tirosinato.
Em consequência, ocorre o aumento da absorvância entre os 280nm e 310nm. Este
aumento sobrepõe-se à variação observada no espectro quando ocorre desenrolamento
da proteína sem ionização da Tyr (diminuição da absorvância entre os 285nm e 295nm
devido ao deslocamento do espectro de absorção da tirosina para a zona do vermelho),
sendo assim necessárias quantidades menores de proteína nas amostras para se
observarem resultados, daí se monitorizar a desnaturação da proteína através dos
resíduos ionizados [1].
Para efectuar este estudo assumiu-se que a absorvância da proteína resulta da soma
das absorvâncias dos resíduos aromáticos que a constituem.
Traçando o gráfico de absorção para cada um dos comprimentos de onda (250nm e
278nm), em função da temperatura no intervalo estudado, verifica-se que a 278nm não
ocorrem grandes variações no espectro de absorvância (porque o fenol e o fenolato
possuem igual coeficiente de absortividade molar para este comprimento de onda, ou
seja, absorvem de forma semelhante [1]). Portanto, este comprimento de onda vai ser
usado como referência para calcular a razão αprot/α. Esta razão corresponde ao grau de
exposição das Tyr na superfície da proteína, com o aumento da temperatura, em que
αprot é o grau de ionização das Tyr (experimental).
Sabendo que ao comprimento de onda de 278nm a Phe possui espectro de absorção
nulo podemos então aproximar a lei de Lambert-Beer
e formular a absorvância da proteína a 250nm
2
(1)
!
!
!
' & "# 1 % & "
!
!
(2)
em que ε NATyr ( OH ) A , ε NATyr (O − ) A , ε NATrpA e ε NAPhe são os coeficientes de absorção molar de
NATyrA (N-acetil-L-tirosinamida) a pH 7,7, NATyrA a pH 12,4, NATrpA (N-acetil-Ltriptofanamida) e NAPhe (N-acetil-L-fenilalanina) respectivamente [1].
No entanto esta formulação é muito afectada pelo erro associado à concentração da
proteína (note-se que, a absorvância é proporcional à concentração de proteína – Lei de
Beer1). Assim, ao se realizarem os cálculos a dois comprimentos de onda, recorrendo-se
à razão A250/A278 para a obtenção do valor de αprot (sendo que um é o de referência),
pretendeu-se eliminar o efeito da concentração de proteína nos resultados (elimina-se a
dependência do factor de concentração). Deste modo [1]
& ()*)+,-,
(,.
(3)
onde
!
/ "# !
0 !
1 !
2 (4)
!
3 !
4 " ' Cada termo da equação é expresso em função da absorvância das diferentes espécies
aos dois comprimentos de onda. É então necessário conhecer a priori os valores
experimentais da Abs250 e de Abs278, bem como o número de cada tipo de aminoácidos
aromáticos da proteína e a absortividade molar, ε, de cada uma das espécies.
Quando a proteína se encontra num estado desnaturado ideal com os resíduos
isolados pelo solvente espera-se que os resíduos de Tyr se comportem como NATyrA e
assim o grau de ionização é dado pela equação de Henderson-Hasselbalch, que
relaciona o pH com o pK de uma determinada espécie [1]
&
5!67'68
5)5!67'68
Assim, a razão entre o grau da ionização do fenol na proteína (αprot) e o previsto pela
relação de Henderson-Hasselbalch (α) descreve o grau de exposição dos resíduos de
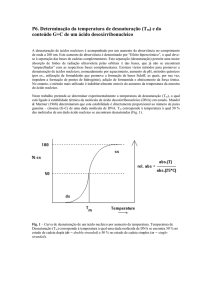
tirosina ao meio. Na figura 2 apresenta-se uma curva típica da variação desta razão com
a temperatura.
1
Princípio de Beer (1852): a absorvância é directamente proporcional à concentração da substância em
solução.
3
(5)
Figura 2. Curva de desnaturação térmica (linha contínua) para a α-quimotripsina [1].
A forma sigmóide da curva, permite-nos afirmar que o processo de desenrolamento
(ou desnaturação) da proteína é um processo cooperativo. Com o aumento da
temperatura há interacções intramoleculares responsáveis pela manutenção da estrutura
tridimensional da proteína que vão enfraquecendo progressivamente. Contudo, a
estrutura mantém-se até certo instante, instante esse em que se desfaz uma ligação que é
determinante neste processo de desnaturação. A partir daí, quebram-se todas as outras
ligações e rapidamente se atinge a desnaturação da proteína, perdendo esta a sua
actividade biológica.
Neste processo, há uma temperatura para a qual existem 50% de moléculas na forma
nativa e 50% na forma desnaturada, designada de temperatura de ponto médio
(temperature at the midpoint – Tm), assim como temperatura de desnaturação ou de
transição.
Exprime-se então a razão de absorvância, αprot/α (assumindo que o processo de
desnaturação é reversível) apenas em função da fracção desnaturada deste processo, fD,
96:;<
9
=
96:;<
9
> . 4 =
96:;<
9
> . 4@ DEEEEEF 4@ @
.A B5,.C
G6:;<
G6:;<
,=
>
G
G
A
G6:;<
G6:;<
=
> ,=
>
G
G
C
A
(6)
onde (αprot/α)N e (αprot/α)D representam a variação da absorvância com a temperatura
nos estados nativo e desnaturado respectivamente (expressão resultante da aproximação
linear feita a cada um dos “patamares” observáveis na representação gráfica de αprot/α
em função da temperatura, correspondentes a cada um dos estados da proteína –
patamar inferior: estado nativo; patamar superior: estado desnaturado) e fN e fD
representam as fracções de proteína nativa e desnaturada, respectivamente, para cada
temperatura.
Obteve-se em seguida a constante de equilíbrio, Keq, do processo de desnaturação da
proteína
.
HI 5,.C
C
(7)
A partir da relação da termodinâmica calculou-se a variação de energia livre de
Gibbs, ∆G, associado a este processo
∆K %L. M. HI 4
(8)
onde R é a constante dos gases perfeitos (1.98720 cal.mol-1.K-1) e T a temperatura
(em K).
Foi depois possível obter a temperatura de desnaturação, Tm, que corresponde ao
ponto em que ∆G=0 no gráfico da variação da energia livre do processo em função da
temperatura. Desta forma foi possível obter também os valores da variação de entalpia,
∆H, e de entropia, ∆S, na temperatura de desnaturação através da expressão
∆K ∆N % M. ∆O
1.2. Método Experimental
Relativamente à sua componente prática, este trabalho é bastante simples e ao
mesmo tempo útil de utilizar.
Basicamente, ele consiste em solubilizar a α-quimotripsina num tampão carbonatobicarbonato (pré termostatizado a 25ºC) e colocar no reactor. Depois, medindo a
temperatura, a cada elevação térmica de 1ºC retira-se uma amostra de 1ml da solução,
até aos 60ºC.
Este procedimento terá de ser repetido para os vários valores de pH da solução
tampão.
No final obtêm-se os valores das absorvâncias provenientes da espectroscopia de UV
nos 250 e 278nm.
2. TRATAMENTO DE RESULTADOS
A partir dos resultados obtidos da espectrofotometria de UV foi possível calcular o
αprot através da equação 3. A equação foi aplicada aos vários valores de absorvâncias,
medidos através dos dois comprimentos de onda, às várias temperaturas. Através da
equação 5 calculou-se, também, o valor de α.
Com estes valores foi possível obter um gráfico que relaciona o quociente αprot/α
com a temperatura (figura 3).
5
(9)
Figura 3. Gráficos de relação entre o quociente αprot/α e a temperatura (K) aos pH’s de 9,8 (ο), 10,2
(*), 10,6 (×) e 11 (É).
De forma a obter os quocientes entre os graus de ionização do fenol quando a
proteína está na forma naturada, (αprot/α)N, e desnaturada, (αprot/α)D, analisaram-se os
gráficos da figura 3. Através dos patamares inferior e superior é possível obter rectas de
ajuste aos pontos. Estas rectas são obtidas por regressão linear em software apropriado.
Assim obtêm-se as várias equações que são representadas graficamente na figura 4,
5, 6 e 7. A valores inferiores de temperatura (verde) estão representadas as equações
correspondentes ao estado de proteína naturada enquanto que, a valores mais elevados
(azul) corresponde o estado de proteína desnaturada.
6
Figura 5. Gráfico representativo da relação
entre αprot/α e a temperatura (K) (ο) e das rectas
de ajuste, por regressão linear, de (αprot/α)N
(verde) e (αprot/α)D (azul) em função da
temperatura (K), a pH 10,2. As equações das
rectas de ajuste são, respectivamente,
PQRST
=
> 0,0006266 M % 0,011156 e
Figura 4. Gráfico representativo da relação
entre αprot/α e a temperatura (K) (ο) e das rectas
de ajuste, por regressão linear, de (αprot/α)N
(verde) e (αprot/α)D (azul) em função da
temperatura (K), a pH 9,8. As equações das
rectas de ajuste são, respectivamente,
PQRST
=
> 0,0072966 M % 2,0285 e
=
P
N
PQRST
P
N
PQRST
=
> 0,011296 M % 2,7879
P
D
Figura 6. Gráfico representativo da relação
entre αprot/α e a temperatura (K) (ο) e das rectas
de ajuste, por regressão linear, de (αprot/α)N
(verde) e (αprot/α)D (azul) em função da
temperatura (K), a pH 10,2. As equações das
rectas de ajuste são, respectivamente,
P
= QRST> 0,00018084 M % 0,40581 e
P
> 0,015324 M % 4,2585.
D
Figura 7. Gráfico representativo da relação
entre αprot/α e a temperatura (K) (ο) e das rectas
de ajuste, por regressão linear, de (αprot/α)N
(verde) e (αprot/α)D (azul) em função da
temperatura (K), a pH 10,2. As equações das
rectas de ajuste são, respectivamente,
PQRST
=
> 0,0013926 M % 0,025663 e
P
N
PQRST
=
P
P
N
PQRST
> 0,0093924 M % 2,0682.
=
D
P
> 0,006068 M % 0,97215.
D
Por forma a obter a constante de equilíbrio, Ku/f, é necessário calcular previamente a
fracção de α–quimotripsina desnaturada, fD. Recorrendo à expressão (6), calculam-se as
fD para cada valor de temperatura, em cada pH. Estes valores estão representados nos
gráficos da figura 8.
Aplicando a equação (7) obtém-se o valor da Ku/f, também para cada instante
térmico.
7
Figura 8. Representação dos pontos da fracção de α–quimotripsina desnaturada, fD, em função da
temperatura. Mais uma vez estes valores são apresentados relativos aos pH’s 9,8 (ο), 10,2 (*), 10,6 (×) e
11 (Ñ).
Recorrendo à termodinâmica, obtém-se facilmente a variação da energia de Gibbs,
ΔG, através da sua relação directa com a constante de equilíbrio e a temperatura, dada
pela equação (8).
a)
b)
Figura 9. Representação dos pontos da ΔG (kcal.mol-1) em função da temperatura, a) em toda a gama
de temperatura considerada na experiência (25 a 60ºC) e b) apenas numa zona considerada linear. Foram
considerados os valores para os 4 pH’s: 9,8 (ο), 10,2 (*), 10,6 (×) e 11 (Ñ).
8
Por análise dos gráficos da figura 9 a) é possível reconhecer uma gama de
temperaturas em que os valores da energia de Gibbs aproximam uma recta linear. Esta
zona (figura 9 b)) é chamada de zona linear e é através desses pontos que se irá traçar
uma recta de ajuste, obtida por regressão linear (figura 10, 11, 12 e 13). Estas rectas são
definidas pelas equações (9).
Figura 10. Variação da energia de Gibbs em
função da temperatura, como recta de ajuste aos
pontos experimentais. O intervalo de
temperatura considerado para a regressão foi
entre 310,15 e 323,15. pH = 9,8.
Figura 11. Variação da energia de Gibbs em
função da temperatura, como recta de ajuste aos
pontos experimentais. O intervalo de
temperatura considerado para a regressão foi
entre 313,15 e 321,15. pH = 10,2.
Figura 12. Variação da energia de Gibbs em
função da temperatura, como recta de ajuste aos
pontos experimentais. O intervalo de
temperatura considerado para a regressão foi
entre 314,15 e 320,15. pH = 10,6.
Figura 13. Variação da energia de Gibbs em
função da temperatura, como recta de ajuste aos
pontos experimentais. O intervalo de
temperatura considerado para a regressão foi
entre 307,15 e 321,15. pH = 11.
A temperatura de transição é facilmente obtida por simples intersecção das rectas de
ajuste com o eixo dos xx (temperatura). Desta forma, obtêm-se os valores apresentados
na tabela 1.
9
pH
9,8
10,2
10,6
11
Tm (ºC)
42,2519
40,8069
40,4968
39,8676
Tabela 1. Temperaturas de transição nos vários pH’s.
Pela equação (9), os valores da variação de entalpia e entropia no ponto da
temperatura de transição estão automaticamente determinados, como sendo o declive e a
ordenada na origem, das equações das rectas de ajuste determinadas anteriormente.
Assim, obtêm-se os valores da tabela 2.
pH
9,8
10,2
10,6
11
ΔHm (kcal.mol-1)
114,88
118,05
126,04
117,47
ΔSm (kcal.mol-1.deg-1)
-0,36181
-0,37310
-0,39755
-0,37319
Tabela 2. Variação da entalpia e entropia no ponto médio, nos vários pH’s.
3. DISCUSSÃO DE RESULTADOS
Em todos os gráficos da variação do grau de exposição das Tyr (αprot/α) com a
temperatura (figura 3) é visível uma curva sigmóide (numa visão aproximada) que
traduz o efeito cooperativo do processo de desnaturação, já referido. Há inicialmente
uma variação muito pouco significativa, correspondente ao momento em que a proteína
ainda se encontra na forma nativa. Nesta altura os efeitos do aumento de temperatura
são quase imperceptíveis, ou seja, a exposição dos resíduos de tirosina ao solvente é
ainda reduzida e não varia consideravelmente. Isto deve-se ao facto da estrutura da
proteína não estar significativamente alterada. A partir de certa temperatura o grau de
exposição das Tyr aumenta bruscamente (principalmente para os valores de pH mais
elevados). Passada esta grande variação, tem-se novamente uma variação pouco
perceptível do grau de exposição das Tyr com o aumento da temperatura. Desta vez,
deve-se ao facto de praticamente todos os resíduos de tirosina estarem expostos ao
solvente.
Observa-se então, que à medida que o pH se torna mais alcalino as oscilações nas
curvas diminuem, bem como a transição para o estado mais próximo do desnaturado se
revela mais rápida. De facto, sendo o pH óptimo desta enzima 8,0 [2] (menor que os
estudados), é de esperar que, para valores de pH maiores e, com o aumento da
temperatura, a proteína perca a estabilidade mais rapidamente.
Para os valores de pH de 9,8 notam-se oscilações em praticamente toda a curva e a
passagem para um estado totalmente desenrolado pode-se considerar lenta, quando
comparada com os outros gráficos. Nestes, as oscilações continuam a ser perceptíveis,
contudo com o aumento do pH, elas acontecem mais para zonas de temperaturas mais
baixas, quando a proteína ainda está na forma nativa. Verifica-se então que, com o
aumento do pH as curvas se vão identificando cada vez mais com a curva apresentada
na figura 2, obtendo-se portanto, uma avaliação da desnaturação mais exacta, devido à
maior percentagem de ionização das Tyr expostas.
Atendendo agora à variação das curvas de variação de fracção desnaturada, fD, com a
temperatura, verificamos que à medida que o pH aumenta, as curvas se deslocam para a
esquerda, tal como era esperado. Isto ocorre como consequência da temperatura de
transição ser cada vez menor, confirmando novamente que, à medida que o pH aumenta
10
mais fácil é provocar a desnaturação da proteína por temperatura, isto é, menor é a sua
estabilidade térmica.
Quanto à representação gráfica das energias livres de Gibbs é importante salientar o
facto de os declives serem negativos em todos eles, como seria de esperar. Isto porque,
para que a proteína se desnature é necessário que o processo se torne favorável (ΔG
negativos).
Quanto aos valores da variação de entropia e entalpia à temperatura de desnaturação,
verifica-se que estes não variam substancialmente com o pH (tendo em conta a sua
ordem de grandeza). Deste modo é possível comparar estes valores (tabela 2) com os da
bibliografia [1]. Para um pH de 10,0, os valores teóricos apresentam um ΔSm de
120kcal.mol-1 e um ΔHm de 0,38kcal.mol-1.deg-1. Confrontando os valores, conclui-se
que estes são muito semelhantes.
Ainda assim, analisando o valor de ΔHm (assim como ΔSm) numa ordem de grandeza
abaixo, observa-se um aumento de ∆Hm com o aumento do pH (que não se verificou
apenas para pH de 11,0), que surge como consequência de ser necessário fornecer mais
energia ao sistema para que ocorra a alteração conformacional proteica. Já o aumento de
∆Sm (que, novamente, não se verificou apenas para pH de 11,0) revela uma maior
desorganização do sistema e consequente reestruturação do solvente.
Quanto à Tm, por observação geral dos gráficos obtidos, nomeadamente o gráfico das
variações da fracção de proteína desnaturada com a temperatura (figura 8), verificamos
que à temperatura de transição a fracção de proteína desnaturada é de aproximadamente
0,5 em cada um dos pH estudados, como seria de esperar, uma vez que nesta fase
metade das moléculas proteicas presentes na amostra se encontram no estado nativo (a
outra metade no estado desnaturado).
Relativamente aos valores numéricos obtidos, e apresentados na tabela 1, é possível
verificar que estes diminuem com o aumento do pH. Esta conclusão vem de encontro ao
que foi dito para as curvas de fD, ou seja, com o aumento do pH as curvas tendem a
deslocar-se para a esquerda, o que faz com que a temperatura ao qual se dá a transição
do estado naturado para o desnaturado seja menor.
Apesar dos bons resultados numéricos, há a salientar que grande parte dos cálculos
foram obtidos com recurso a dados aproximados. Assumiu-se que o valor do pK
característico da ionização das Tyr era constante e igual a 10,1 (a 25ºC) e que a proteína
funcionava como a soma dos seus aminoácidos aromáticos.
Em suma, pode-se concluir que a metodologia utilizada para estudar a estabilidade
térmica da α-quimiotripsina, para além de ser simples e pouco dispendiosa, é eficaz,
uma vez que através dela se obtiveram resultados bastante aceitáveis.
11
4. BIBLIOGRAFIA
[1] Thermal unfolding of proteins at high pH range studied by UV absorbance.
Melo, E. Pinho et al. s.l. : Elsevier Science B.V., 1997. Journal of biochemical
and biophysical methods. Vol. 34, pp. 45-59.
[2] Nelson, David L. e Cox, Michael M. Lehninger: Principles of Biochemistry. 4ª.
New York : W. H. Freeman and Company, 2005. pp. 213-215.
12