PDF - ELITE CAMPINAS

(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE IME 2007 – FÍSICA – QUESTÕES DISCURSIVAS
em 28,8 μJ . Considerando que a resistência por unidade de
comprimento do fio resistivo é constante, determine a massa
específica do líquido que substituiu a água.
Dados: aceleração da gravidade (g) = 10 m/s2;
massa específica da água ( μa ) = 1 g/cm3.
FÍSICA
QUESTÃO 1
No instante t = 0, uma fonte sonora que gera um tom com freqüência
500 Hz é arremessada verticalmente do solo com velocidade inicial 40
m/s. Pede-se:
a) a maior e a menor freqüência do som ouvido por um observador
estacionário situado muito próximo do local do arremesso;
b) um esboço do gráfico da freqüência ouvida pelo observador em
função do tempo após o lançamento para 0 < t < 10 s.
Dados: aceleração da gravidade (g) = 10 m/s2
velocidade do som (vs) = 340 m/s
Obs.: despreze o atrito da fonte sonora com o ar e suponha que a
fonte permaneça imóvel após atingir o solo.
c
b
K
a
M
Resolução
a) As variações de freqüência são devidas ao efeito Doppler, assim:
- A menor freqüência é percebida no afastamento da fonte, no
instante t=0 , em que a velocidade é máxima. Logo:
fo
fF
=
Vs ± Vo
Vs ± VF
C1 = 10 μF
R1 = 1Ω
H
24 V
Resolução
O sinal correto é determinado pela convenção de sinais da figura
abaixo:
Na primeira situação, com o tanque preenchido com água e a chave K
aberta, temos um circuito com a fonte (E = 24 V) e dois resistores
( R1 = 1Ω e Rab ) associados em série. A corrente que percorre esse
+
circuito é dada a partir da potência dissipada em 1:
Pot1 = R1 ⋅ i12 ⇒ 16 = 1⋅ i12 ⇒ i1 = 4A .
F
Então, a resistência
o
Rab
pode ser determinada por:
E = (R1 + Rab ) ⋅ i1 ⇒ 24 = (1 + Rab ) ⋅ 4 ⇒ Rab = 5Ω
Assim:
Agora vamos substituir a água pelo líquido mais denso e fechar a
chave K. Após um longo intervalo de tempo, quando o capacitor já
estiver totalmente carregado, não haverá mais corrente passando
através dele, e novamente teremos um circuito com a fonte e dois
resistores ( R1 = 1Ω e Rab ' ) associados em série, onde Rab ' é a
fo
500
340.500
=
⇒ fo =
⇒ fo = 447 Hz
340 + 0
340 + 40
380
- A maior freqüência é percebida na aproximação da fonte, no ponto
onde a velocidade é máxima (no retorno da fonte à origem).
Sabendo que metade do tempo total é o tempo para a fonte chegar na
altura máxima, onde a velocidade é nula, temos:
v1/2 = v0 – g.t1/2 ⇒ 0 = 40 – 10.t1/2 ⇒ t1/2=4s ⇒ ttotal=8s
Neste ponto o módulo da velocidade é igual ao da velocidade inicial,
no sentido contrário.
fo
500
340.500
=
⇒ fo =
⇒ fo = 567 Hz
340 + 0
340 − 40
300
b) A fonte sonora se move num MUV, então sua velocidade é dada
pela expressão:
VF (t) = 40-10.t
nova resistência determinada pelo cursor metálico.
Como o capacitor está em paralelo com o resistor R1 , ambos estarão
submetidos à mesma diferença de potencial, que pode ser calculada
pela energia acumulada no capacitor:
E=
C ⋅ U2
10 ⋅ 10−6 ⋅ U2
⇒ 28,8 ⋅ 10−6 =
⇒ U = 2,4V
2
2
Assim:
Portanto, a nova corrente no circuito é calculada por:
U = R1 ⋅ i ⇒ 2,4 = 1⋅ i ⇒ i = 2,4A
fo
500
34.500
=
⇒ fo =
340 + 0
340 + (40-10.t)
38-t
A partir daí, podemos construir o seguinte esboço:
Assim, determinamos R:
E = (Rab '+ R1) ⋅ i ⇒ 24 = (Rab '+ 1) ⋅ 2,4 ⇒ Rab ' = 9Ω
f (Hz)
Usando a informação do enunciado que a resistência por unidade de
comprimento é constante, vem que:
Rab Rab '
5
9
=
⇒
= ⇒ A ' = 0,18m
A
A'
0,1 A '
Agora, analisando o empuxo em cada situação, observamos que em
ambos os casos o empuxo deve equilibrar o peso do bloco. Como o
peso do bloco não muda, os empuxos nas duas situações devem ser
de mesma intensidade:
G
G
G
G
| E1 |=| E2 |⇒ V1 ⋅ ρ A ⋅ | g |= V2 ⋅ ρL ⋅ | g | ,
onde
ρA
e
ρL
são
567
500
447
4
8
10 t (s)
QUESTÃO 2
respectivamente as densidades da água e do líquido mais denso.
Chamando de S área da base do bloco e de h1 e h2 as alturas da
A figura ilustra um bloco M de madeira com formato cúbico,
parcialmente submerso em água, ao qual está fixado um cursor
metálico conectado a um circuito elétrico. Na situação inicial, a face do
fundo do bloco se encontra a 48 cm da superfície da água, a chave K
está aberta e o capacitor C1 descarregado. O comprimento do fio
resistivo entre a posição b do cursor metálico e o ponto a é 10 cm. A
potência dissipada no resistor R1 é 16 W.
Em determinado instante, a água é substituída por outro líquido mais
denso, mantendo-se constante o nível H da coluna de água
inicialmente existente. Fecha-se a chave K e observa-se que, após um
longo intervalo de tempo, a energia armazenada em C1 se estabiliza
parte submersa nas situações anterior e posterior respectivamente,
temos:
G
G
h
(S ⋅ h1) ⋅ ρ A ⋅ | g |= (S ⋅ h2 ) ⋅ ρL ⋅ | g |⇒ ρL = 1 ⋅ ρ A
h2
Para determinar a nova altura h2 do cilindro, fazemos:
h1 − h2 = A '− A ⇒ 0,48 − h2 = 0,18 − 0,10 ⇒ h2 = 0,4m
Então, finalmente, ρL =
1
0,48
⋅ 1,0 = 1,2g / cm3
0,4
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE IME 2007 – FÍSICA – QUESTÕES DISCURSIVAS
QUESTÃO 3
QUESTÃO 4
Uma mola com constante elástica k, presa somente a uma parede
vertical, encontra-se inicialmente comprimida em 10 cm por um bloco
de massa m = 4 kg, conforme apresenta a figura abaixo. O bloco é
liberado e percorre uma superfície horizontal lisa OA sem atrito. Em
seguida, o bloco percorre, até atingir o repouso, parte da superfície
rugosa de uma viga com 4 m de comprimento, feita de material
uniforme e homogêneo, com o perfil mostrado na figura. Sabendo que
a força normal por unidade de área no tirante CD de seção reta 10
mm2 é de 15 MPa na posição de repouso do bloco sobre a viga,
determine o valor da constante elástica k da mola.
Dados: pesos por unidade de comprimento da viga (PL1) = 20 N/m e
(PL2) = 40 N/m; coeficiente de atrito cinético ( μ c ) = 0,50;
Um pequeno corpo é abandonado com velocidade inicial nula no ponto
A de uma rampa, conforme ilustra a Figura 1. No instante em que esse
corpo passa pelo ponto P, um dispositivo provoca o fechamento da
chave S1 do circuito elétrico apresentado na Figura 2.
No instante em que o resistor R1 desse circuito atinge o consumo de
0,05 W.h, um percussor é disparado, perpendicularmente ao trecho BC, com o objetivo de atingir o corpo mencionado. Sabe-se que ao
percorrer a distância d mostrada na Figura 1, o corpo tem sua
velocidade reduzida a 1/3 da alcançada no ponto B. Considerando que
os trechos A-B e P-C não possuem atrito e que o corpo permanece em
contato com o solo até o choque, determine o ângulo de inclinação θ
da rampa para que o corpo seja atingido pelo percussor.
Dado: aceleração da gravidade (g) = 10 m/s2.
aceleração da gravidade (g) = 10 m/s2;
1 Pa = 105 N/m2.
A
Obs.: o tirante não prejudica o movimento do bloco.
percussor
2,5 m
θ
B
P
D
C
10 m
d
k
m
Figura 1
P L1
O
1,2Ω
4Ω
2,8Ω
apoio
C
viga
P L2
A
B
2,0 m
2,0 m
Resolução
NOTA: Há um erro no enunciado desta questão que pode ter
prejudicado muitos candidatos, o qual consistiu em afirmar que 1 Pa =
105 N/m2, quando o correto seria 1Pa = 1N/m2.
Utilizando-se a informação correta, temos:
G
G
Peso do bloco: | P |= m⋅ | g |= 4 ⋅ 10 = 40N
Na posição de equilíbrio do bloco, a força aplicada pelo tirante CD
G
vale: | FT |= p ⋅ A = (15 ⋅ 10 6 ) ⋅ (10 ⋅ 10 −6 ) = 150N
G
G
Chamando de P1 e P2 os pesos das vigas dos lados esquerdo e
Figura 2
Resolução
No circuito, a resistência equivalente será
4 ⋅ (1,2 + 2,8)
REQ =
= 2Ω
4 + (1,2 + 2,8)
Ao fecharmos a chave S1 , a corrente que aparece no circuito é
i=
rugosa
lisa
R1
S1
20 V
tirante
bloco
E
20
=
= 10A . Como ambos os trechos em paralelo no circuito
REQ
2
direito respectivamente, temos:
G
N
| P1 |= 20 ⋅ 2m = 40N
m
G
N
| P2 |= 40 ⋅ 2m = 80N
m
Seja x a distância percorrida pelo bloco a partir do ponto A até parar,
de acordo com a figura:
possuem uma resistência igual ( 4Ω ), a corrente será dividida
igualmente entre os dois trechos, ou seja, cada resistor é percorrido
por uma corrente de 5A . Logo, a potência dissipada no resistor de
1,2Ω é
2
⎛ i⎞
Pot = R ⋅ ⎜ ⎟ = 1,2 ⋅ 52 = 30W
⎝2⎠
O tempo decorrido para que este resistor dissipe os 0,05W ⋅ h é:
G
FT
2,0 m
G
N
E
0,05W ⋅ h
1
1
Pot = DISSIP ⇒ 30W =
⇒ Δt =
h=
⋅ 3600s = 6s
Δt
Δt
600
600
x
Durante esse intervalo de tempo de 6 s o corpo deve percorrer o
trecho PC, ou seja, deve percorrer 10 m.
Assim, a velocidade no trecho PC é:
v
1
PC 10 5
VPC =
=
= m / s . Como PC = ⇒ vB = 3 ⋅ vPC = 5 m
s
vB
3
Δt
6
3
A
Ou seja, partindo do repouso em A, o corpo acelera até o ponto B
atingindo nesse ponto uma velocidade de 5 m/s.
Para descobrir a aceleração no trecho AB, vamos impor que a força
resultante no plano inclinado sem atrito é a componente do peso na
direção da rampa:
G
G
G
G
G
| FRES |=| P | ⋅senθ ⇒ m⋅ | a |= m⋅ | g | ⋅senθ ⇒ | a |=| g | ⋅senθ
B
G
P1
G
PB
1,0 m
G
P2
Como o movimento no trecho AB é uniformemente variado
(aceleração constante), da equação de Torricelli:
v 2 = v 02 + 2 ⋅ a ⋅ Δs ⇒ 52 = 02 + 2 ⋅ (10 ⋅ senθ ) ⋅ 2,5 ⇒
senθ =
3,0 m
Impondo o equilíbrio dos torques em relação ao ponto B, temos:
G
G
G
G
G
| P1 | ⋅3+ | PB | ⋅( 4 − x )+ | P2 | ⋅1 =| FT | ⋅2+ | N | ⋅0 ⇒
1
⇒ θ = 30°
2
2
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE IME 2007 – FÍSICA – QUESTÕES DISCURSIVAS
40 ⋅ 3 + 40 ⋅ ( 4 − x ) + 80 ⋅ 1 = 150 ⋅ 2 ⇒ x = 1,5m
Durante o movimento do bloco ao longo desses 1,5 m na superfície
rugosa da viga, a desaceleração a que ele está submetido é:
G
G
G
G
G
FRES = FAT ⇒ m | ⋅a |= μ ⋅ m⋅ | g |⇒| ⋅a |= 0,5 ⋅ 10 = 5m / s 2
Desse modo, a potência que o resistor RA irá dissipar é:
Q 57,6 ⋅ 10 3 J
Pot =
=
= 32W
Δt
30 ⋅ 60s
Quando a chave é S1 fechada, a corrente que passa pelo amperímetro
(i0 = 2A) é a mesma corrente que passa pelo resistor RA. Logo:
Pela equação de Torricelli: v 2 = v 0 + 2 ⋅ a ⋅ Δs ⇒
2
Pot = R A ⋅ i 0 ⇒ 32 = R A ⋅ 22 ⇒ R A = 8Ω
2
0 = v 0 + 2 ⋅ ( −5) ⋅ 1,5 ⇒ v 0 = 15(m / s )
2
2
2
2
2
b) Estando S1 fechada e S2 ainda aberta, temos que:
E = (RS + R A ) ⋅ i 0 ⇒ 24 = (RS + 8) ⋅ 2 ⇒ RS = 4Ω
Impondo a conservação da energia mecânica no trecho liso:
2
k ⋅ x mola
m ⋅v0
=
2
2
2
3
k ⋅ (0,1) = 4 ⋅ 15 ⇒ k = 6 ⋅ 10 N / m
2
c) Quando fechamos a segunda chave (S2), ou seja, estando ambas
as chaves (S1 e S2) fechadas, teremos um circuito onde o resistor S2 é
percorrido pela nova corrente total i = 2,4 A, e esta se divide em duas
partes i A e i B , que percorrem respectivamente os resistores R A e
E O = E A ⇒ E ELÁSTICA = E CINÉTICA ⇒
RB (com i A + i B = i ).
QUESTÃO 5
Estando os resistores R A e RB em paralelo, ambos estão submetidos
A figura 1 ilustra uma bateria, modelada através de uma fonte de
tensão elétrica VF em série com um resistor RS, conectado a um
voltímetro V, cuja leitura indica 24 V. Essa bateria é ligada em série
com o amperímetro A e com um circuito composto por uma resistência
de aquecimento RA em paralelo com uma resistência RB, conforme
mostra a Figura 2. A resistência RA encontra-se imersa em 0,2 L de
um líquido com massa específica de 1,2 g/cm3.
Inicialmente, as chaves S1 e S2 da Figura 2 encontram-se abertas. A
chave S1 é acionada. Observa-se que o amperímetro indica 2A e que
a temperatura do líquido se eleva de 10 °C para 40 °C em 30 minutos.
Em seguida, a chave S2 é fechada e o amperímetro passa a indicar
2,4 A. Considerando que não exista perda de energia no aquecimento
da água e que o voltímetro e o amperímetro sejam ideais, determine:
a) a resistência RA em ohms;
b) a resistência RS em ohms;
c) a resistência RB em oms.
Dados:
calor específico do líquido (c) = 2 cal/(g .°C); 1 cal ≅ 4 J
Bateria
RS
à mesma diferença de potencial, que vale:
U A = U B = E − RS ⋅ i = 24 − 4 ⋅ 2,4 = 14,4V
Assim, U A = R A ⋅ i A ⇒ 14,4 = 8 ⋅ i A ⇒ i A = 1,8 A
Em RB , temos: i B = i − i A = 2,4 − 1,8 = 0,6 A ,e portanto:
U B = RB ⋅ i B ⇒ 14,4 = RB ⋅ 0,6 ⇒ RB = 24Ω
QUESTÃO 6
Uma massa m de ar, inicialmente a uma pressão de 3 atm, ocupa 0,1
m3 em um balão. Este gás é expandido isobaricamente até um volume
de 0,2 m3 e, em seguida, ocorre uma nova expansão através de um
processo isotérmico, sendo o trabalho realizado pelo gás durante esta
última expansão igual a 66000 J. Determine
a) o trabalho total realizado em joules pelo gás durante todo o
processo de expansão;
b) o calor total associado às duas expansõoes, interpretando
fisicamente o sinal desta grandeza.
Cp
kgf
; 1 kgf = 10 N ; γ =
= 1,4
Dados: 1 atm = 1
2
C
cm
v
Obs.: suponha que o ar nestas condições possa ser considerado como
gás ideal.
+
VF
V
–
Resolução
Figura 1
Bateria
RS
S1
S2
A
RA
+
VF
RB
–
Figura 2
a) O trabalho total realizado durante todo o processo de expansão
será dado por τtotal = τ12 + τ23
Resolução
a) Quando colocamos o voltímetro nos extremos da bateria, não
haverá corrente circulando, pois o voltímetro é ideal (resistência
infinita). Assim, a indicação do voltímetro é a fem (E) da bateria, já que
não haverá queda de tensão na resistência interna.
Logo, E = 24V .
A densidade do líquido é: ρ L = 1,2g / cm 3 = 1,2kg / L
onde:
τ12 é o trabalho da transformação isobárica;
τ23 é o trabalho da transformação isotérmica.
Logo:
τ12 = P. ΔV = 3 atm ⋅ 0,1 m3 = 3 ⋅ 105
N
⋅ 0,1 m3 ⇒ τ12 = 30 kJ
m2
Considerando τ23 = 66 kJ (do enunciado), temos
τtotal = 30 + 66 ⇒ τtotal = 96 kJ
A massa nesse caso é dada por: m = ρ ⋅ V = 1,2 ⋅ 0,2 = 0,24kg
O calor específico sensível do líquido é:
cal
J
4J
c=2
= 2 −3
= 8 ⋅ 10 3
g ⋅ °C
kg ⋅ °C
10 kg ⋅ °C
O calor necessário para elevar a temperatura do líquido de 10ºC para
40ºC é:
Q = m ⋅ c ⋅ Δθ = 0,24 ⋅ 8 ⋅ 10 3 ⋅ ( 40 − 10 ) = 57,6 ⋅ 10 3 J
b) O calor total trocado durante todo o processo de expansão será
dado por Qtotal = Q12 + Q23
onde:
Q12 é o calor trocado na transformação isobárica;
3
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE IME 2007 – FÍSICA – QUESTÕES DISCURSIVAS
b) Logo após bater no obstáculo, temos um movimento circular de raio
R, como ilustra a figura:
Q23 é o calor trocado na transformação isotérmica.
Logo:
Q12 = n ⋅ Cp ⋅ ΔT
L’
Do gráfico temos:
⎧⎪P1 ⋅ V1 = n ⋅ R ⋅ T1
P ⋅ ΔV
⇒ Como P1 = P2 ⇒ ΔT =
⎨
n⋅R
⎪⎩P2 ⋅ V2 = n ⋅ R ⋅ T2
θ = 60
0
Considerando Cp − Cv = R :
Q12 = n ⋅ Cp .
Q12 = n ⋅ Cp ⋅
R
P ⋅ ΔV
P ⋅ ΔV
= n ⋅ Cp ⋅
⇒
n ⋅R
n ⋅ (Cp − Cv )
P . ΔV
⎛
C
n ⋅ Cp ⋅ ⎜ 1 − v
⎜
Cp
⎝
Q12
⇒ Q12 =
⎞
⎟
⎟
⎠
= 105 kJ
Na figura, temos: L’cos60º = 0,2L ⇒ L’= 0,4L, logo:
R = L – 0,4L = 0,6L
Montando o diagrama de forças para a situação dada, temos:
P ⋅ ΔV
30 kJ
=
⎛
Cv ⎞ ⎛ 1 − 1 ⎞
⎜1 −
⎟ ⎜
⎟
⎜
Cp ⎟⎠ ⎝ 1,4 ⎠
⎝
T
Como no processo 2-3 não temos alteração da energia interna, pela
1ª. lei da termodinâmica:
Q23 = τ23 ⇒ Q23 = 66 kJ
60º
Então o calor total trocado será:
Qtotal = 105 + 66 ⇒ Qtotal = + 171 kJ
(M+m) g
Da figura, vem:
O sinal positivo do calor total informa que neste processo de
expansão a massa de ar contida no balão, recebeu calor do meio
externo.
(M + m )v 22
⇒
R
⎛v2 g ⎞
(III)
T = (M + m )⎜⎜ 2 + ⎟⎟
2⎠
⎝R
Mas v2 pode ser calculado pela conservação de energia entre os
instantes 1 e 2:
(M + m )v 12 (M + m )v 22
=
+ (M + m )g (L − L cos 60 0 ) ⇒
2
2
v 22 v 12 gL
=
−
⇒ v 22 = 16 − 10 = 6 (m/s)2
(IV)
2
2
2
T – (M+m)g.cos60º = Rcp =
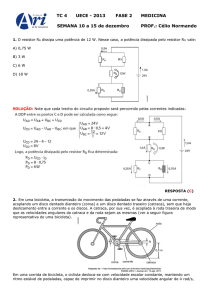
QUESTÃO 7
Um pêndulo com comprimento L = 1 m, inicialmente em repouso,
sustente uma partícula com massa m = 1 kg. Uma segunda partícula
com massa M = 1 kg movimenta-sena direção horizontal com
velocidade constante v0 até realizar um choque perfeitamente
inelástico com a primeira. Em função do choque, o pêndulo entra em
movimento e atinge um obstáculo, conforme ilustrado na figura.
Observa-se que a maior altura alcançada pela partícula sustentada
pelo pêndulo é a mesma do ponto inferior do obstáculo. O fio pendular
possui massa desprezível e permanece sempre esticado.
Considerando a aceleração da gravidade g = 10 m/s2 e a resistência
do ar desprezível, determine:
a) a velocidade v0 da partícula com massa M antes do choque
b) a força que o fio exerce sobre a partícula de massa m
imediatamente após o fio bater no obstáculo.
⎛ 6
⎞
De (III) e (IV): T = 2⎜⎜
+ 5 ⎟⎟ (N ) ⇒ T = 30N
⎝ 0,6
⎠
QUESTÃO 8
Uma partícula de massa m e carga elétrica q é arremessada com
velocidade escalar v numa região entre duas placas de comprimento
G
d, onde existe um campo elétrico uniforme E , conforme ilustra figura.
Ao sair da região entre as placas, a partícula entra numa região sujeita
G
a um campo magnético uniforme B e segue uma trajetória igual a
uma semicircunferência, retornando à região entre as placas. Pede-se:
a) o ângulo θ de arremesso da partícula indicado na figura;
b) a energia cinética da partícula no instante de seu retorno à região
entre as placas;
G
c) a faixa de valores de B para que a partícula volte à região entre as
θ = 60o
G
v0
placas;
d) verificar, justificando, se existe a certeza da partícula se chocar com
alguma das placas após regressar à região entre as placas.
d
q , m
θ
Resolução
a) Como o choque é perfeitamente inelástico, a partícula ficará
“colada” ao pêndulo após a colisão, assim:
Mv0 + m.0 = (M+m)v1
onde v1 é a velocidade do conjunto imediatamente após o choque.
Como M = m = 1 kg, logo:
v1 = v0/2 (I)
Pela conservação de energia:
Ec1 = Ep2
onde 1 é o momento imediatamente após o choque e 2 é o instante
em que o conjunto atinge a altura máxima. Assim, substituindo os
valores:
(M + m )v 12
= (M + m )g (L − 0,2L ) ⇒ v 12 = 1,6gL ⇒ v 1 = 4 m / s (II)
2
Substituindo (II) em (I): v0 = 8 m/s.
v
→
B
→
E
Resolução
Devemos observar que, para percorrer uma trajetória igual a uma
semicircunferência, a partícula deve atingir a região de campo
magnético perpendicularmente a este. Note que isto somente ocorre
se a carga q for positiva.
4
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE IME 2007 – FÍSICA – QUESTÕES DISCURSIVAS
Podemos observar assim, o lançamento obliquo executado pela
partícula sob a ação exclusiva de uma força elétrica vertical, para
cima. Note que se a carga for negativa. Assim:
E..q
Fe = E..q = m.a → a =
m
d
d
d
vx = → t =
=
t
vx
v . cos θ
v y = v 0 y − a.t
E.q
d
.
m v . cos θ
a) Fazendo, vy=0 no momento em que a carga atinge o campo
magnético, temos:
E.q
d
1
E.q d
v .senθ =
.
⇒ sen 2θ =
.
m v . cos θ
2
m v2
v y = v .senθ −
θ =
Como a velocidade horizontal é a mesma na ida e na volta e a
velocidade vertical é nula no ponto de fronteira entre os campos
elétrico e magnético, então, dado que a carga estará sempre sob
mesma aceleração a distância entre as trajetórias sobre um eixo
vertical qualquer é constante e igual a 2R, provocando a colisão no
ponto ilustrado como C, na figura, qualquer que seja R.
⎛ 2.E.q.d ⎞
1
⎟
arcsen ⎜
⎜ m.v 2 ⎟
2
⎝
⎠
QUESTÃO 9
Um explorador especial sofreu um acidente e encontra-se em um
planeta desconhecido. Entre seus equipamentos, ele dispõe de um
telescópio, um dinamômetro, um bloco de massa M conhecida e um
fio de comprimento L. O telescópio é composto por uma objetiva e
uma ocular com distâncias focais f e f’, respectivamente. O explorador
observou a existência de um satélite no céu deste planeta e o
telescópio apresentou uma imagem de diâmetro máximo 2r’. Medidas
anteriores ao acidente indicavam que o raio deste satélite era, na
realidade, R. O astronauta determinou que o período de revolução do
satélite em torno do planeta era equivalente a 5000 períodos de um
pêndulo improvisado com o bloco e o fio. Se o dinamômetro registra
que este bloco causa uma força F sob efeito da gravidade na
superfície do planeta, determine:
a) a massa M em função dos parâmetros fornecidos;
b) o diâmetro D deste planeta em função dos parâmetros fornecidos
Dado: constante de gravitação universal = G
b) No retorno da semicircunferência, novamente vy=0, portanto toda a
Energia cinética está relacionada a vx:
1
1
E c = mv x2 = mv 2 . cos 2 θ , mas
2
2
2 ⎞
⎛
1⎜
1 + cos 2θ
1
⎛ 2.E.q.d ⎞ ⎟
cos2θ =
= ⎛⎜1 + 1 − sen 2 2θ ⎞⎟ = ⎜1 + 1 − ⎜
⎟ ⎟
2
⎠ 2⎜
2
2⎝
⎝ m.v ⎠ ⎟
⎝
⎠
2 ⎞
⎛
⎛ 2.E.q.d ⎞ ⎟
⎜
1
1
+
−
⎜
⎟
⎟
⎜
2
⎜
⎝ m.v ⎠ ⎟
⎠
⎝
c) O raio máximo de semicircunferência deve ser no máximo igual à
metade distância entre as placas (Δh), de acordo com a figura:
logo, Ec =
1
mv 2
4
Resolução
a) Segundo o enunciado, a massa M do corpo é conhecida, admitimos
assim que o examinador tenha pedido a massa MP do planeta.
D/2
Desta forma, supondo B>0 (ou seja, respeitando a orientação de B
indicada na figura):
0=
2
v 0y
2
v 0y
E.q
= 2.a.Δh ⇒ v .sen θ = 2.
.2Rmáx
m
− 2.a.Δh
2
Rmáx =
Consideremos t o período do pêndulo. Temos:
L
L
t = 2π
⇒ t 2 = 4 π2
g
g
m.v 2 .sen2θ
4.E.q
Consideremos T o período do satélite. Pela 3ª lei de Kepler:
T2 =
m.v . cos θ m.v sen θ
<
q.B
4.E.q
2
Como cos2 θ =
Satélite
Planeta
2
m.v x
, então:
Sendo R =
q.B
B > 4.E.
R
d
cos θ
vsen2θ
. = 4.E.
⎛
2
⎛ 2.E.q.d ⎞
1⎜
1+ 1− ⎜
⎟
⎜
2
2⎜
⎝ m.v ⎠
⎝
2
(
Segundo o enunciado, temos
cos θ
2
v 1 − cos θ
)
T2
t
.
Como g =
⎞
⎟ , temos:
⎟
⎟
⎠
2
4 π2 3
d .
GMP
= 50002 =
d3 GMP
d3
g
=
Lg
GMPL
1
F
F
d3F
d3 .
, temos 50002 =
⇒ MP =
M
LGMPM
50002 LGM
Determinaremos d em função dos parâmetros dados. Considere o
seguinte esquema para o telescópio:
⎛
⎛
2⎞
2⎞
⎛ 2.E.q.d ⎞ ⎟
⎛ 2.E.q.d ⎞ ⎟
1⎜
1⎜
+
−
1+ 1− ⎜
1
1
⎟
⎜
⎟
2 ⎜⎜
2 ⎜⎜
⎝ m.v 2 ⎠ ⎟⎟
⎝ m.v 2 ⎠ ⎟⎟
⎝
⎠
⎝
⎠
=
B>
⎛
⎛ ⎛
⎛
2 ⎞⎞
2 ⎞⎞
⎛ 2.E.q.d ⎞ ⎟ ⎟
⎛ 2.E.q.d ⎞ ⎟ ⎟
1
⎜
⎜1
v ⎜1 − ⎜1 + 1 − ⎜
v ⎜ ⎜1 − 1 − ⎜
⎟ ⎟
⎜
⎜
2 ⎟ ⎟⎟
2
2
⎝ m.v ⎠ ⎟ ⎟
⎝ m.v 2 ⎠ ⎟⎟ ⎟
⎜
⎜
⎜ ⎜
⎝
⎠
⎝
⎠⎠
⎝
⎠
⎝
d) Após retornar à região do campo elétrico, a partícula irá descrever
sempre uma trajetória idêntica à sua trajetória de ida, a menos do fato
de que esta trajetória estará deslocada em y de 2R (para cima em
relação à trajetória de ida, ponto a ponto). Veja a figura abaixo:
d-D/2
Fo’
r
Fi’
R
r'
Fi
Ocular
5
Fo
Objetiva
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE IME 2007 – FÍSICA – QUESTÕES DISCURSIVAS
2d
Objetiva:
A distância do satélite à objetiva (d – D/2) é muito maior que a
distância focal da mesma, f. Portanto a imagem conjugada está no
foco imagem da objetiva, Fi na figura.
iOb
p′
−r
f
Rf
=−
⇒ d−D 2 =
(1)
= − Ob ⇒
R
d−D 2
r
oOb
pOb
A
L
Ocular:
A medida do tamanho da imagem fornecida pelo telescópio é r’. Para
escrever r em função de r’ é preciso detalhar a conjugação na ocular.
A distância focal da objetiva é f’. Assim temos
1
1
1
=
+
f ′ pOc p′Oc
E
D
B
Fs
folhas de
papel
d
Para a maior ampliação possível, a imagem virtual formada pela ocular
deve ficar o mais próximo possível do observador, no ponto próximo.
Um observador normal tem ponto próximo a aproximadamente 0,25 m,
portanto:
p′Oc = −0,25 m
Resolução
Observe a figura:
1
1
1
1
f′
⇒ pOc =
⇒ pOc =
(2)
=
+
1 f′ + 4
f ′ pOc −0,25
1 + 4f ′
O aumento linear transversal na ocular permite escrever:
iOc
p′
p r′
r′
−0,25
⇒ r = Oc ⇒ r = 4pOcr ′ (3)
= − Oc ⇒ = −
r
pOc
oOc
pOc
0,25
4f ′r ′
(4)
1 + 4f ′
Telescópio (objetiva + ocular)
Substituindo (4) em (1):
D fR ⎛
1⎞
fR ⎛
1⎞ D
D Rf (1 + 4f ′ )
d− =
⇒ d− =
⎜1 +
⎟ ⇒ d = ′ ⎜1 +
⎟+
2
r′ ⎝
4f ⎠
r ⎝
4f ⎠ 2
2
4f ′r ′
Considerando que o raio do planeta, D/2, possa ser desprezado em
relação à distância do centro do planeta ao satélite, d, temos:
fR ⎛
1⎞
d=
⎜1 +
⎟ ; D << d (5)
r′ ⎝
4f ⎠
Substituindo (2) em (3): r =
Temos finalmente MP =
F ⎡ fR ⎛
1 ⎞⎤
1+
⎟⎥
2 LGM ⎢ r ′ ⎜
4f
⎠⎦
5000
⎣ ⎝
1
3
Da figura acima temos que:
h a
h a
h
+
−
2
2
2
2
tgθ1 =
tgθ 2 =
tgθ = 2
2d
2d
2d
Consideraremos que h >> a , uma vez que a é largura da fenda (da
b) A aceleração da gravidade no ponto do corpo de massa M é:
gP =
GMP
GMPM
F
=
⇒ D=2
.
M ( D 2 )2
F
ordem de grandeza do comprimento de onda) e h é o espaço entre a
placa superior e a face da folha de papel que se encontra no topo da
pilha. Desse modo podemos assumir que tgθ1 ≅ tgθ 2 ≅ tgθ , ou seja,
Substituindo MP por sua expressão determinada no item a obtemos,
após algumas simplificações:
1
1 ⎡ fR ⎛
1 ⎞⎤
D=
⎢ ⎜1 +
⎟⎥
2500 L ⎣ r ′ ⎝
4f ⎠ ⎦
os raios incidentes que interferem destrutivamente para formar o
mínimo de difração de primeira ordem no ponto A são praticamente
paralelos. Então, podemos considerar, que a diferença de caminho
entre os pares de raios que se cancelam é dada por:
3
QUESTÃO 10
Δ=
A figura ilustra uma empacotadora de papel que utiliza um capacitor
de placas quadradas e paralelas para empilhar a quantidade exata de
folhas contidas em cada embalagem. Ao atingir a altura limite do bloco
de papel, o laser L acoplado à fenda simples Fs projeta os mínimos de
intensidade de difração de primeira ordem nos pontos A e B,
eqüidistantes da linha tracejada ED. Sabendo que cada folha de papel
possui uma espessura ef, determine o número de folhas contidas em
cada embalagem.
Dados: comprimento de onda do laser λ;
largura da fenda simples = a;
distância entre a fenda e a reta AB = 2 d
área da superfície das placas do capacitor = d2
permissividade do vácuo = ε0
permissividade do papel = ε
capacitância do capacitor com o limite máximo de folhas de
papel = C
Obs.: despreze o efeito da borda do capacitor
λ
a
λ
⎛λ⎞
senθ = ⇒ senθ = ⇒ cos θ = 1 − ⎜ ⎟
2
2
a
⎝a⎠
cos θ =
a 2 − λ2
⇒ tgθ =
a
2
⇒
λ
a − λ2
2
Logo:
h
=
4d
λ
⇒ h=
a −λ
2
2
4⋅d⋅λ
(I)
a 2 − λ2
O conjunto de folhas junto com o capacitor formam um sistema de dois
capacitores em série (um cujo dielétrico é o papel e outro cujo
A
temos as
dielétrico é o vácuo). Assim, lembrando que C = ε
d
capacitâncias:
d2
d2
e Cvacuo = ε0
H
h
Cpapel.Cvacuo
A capacitância equivalente é dada por: C =
Cpapel + Cvacuo
Cpapel = ε
6
(19) 3251-1012
www.elitecampinas.com.br
O ELITE RESOLVE IME 2007 – FÍSICA – QUESTÕES DISCURSIVAS
ε 0 ⋅ d2 ε ⋅ d2
⋅
2
h
H ⇒ C = ε0 ⋅ ε ⋅ d ⇒
C=
2
ε0 ⋅ H + ε ⋅ h
ε0 ⋅ d
ε ⋅ d2
+
h
H
2
⎞
ε ⎛⎜ ε 0 ⋅ d
C ⋅ ε 0 ⋅ H + C ⋅ ε ⋅ h = ε 0 ⋅ ε ⋅ d2 ⇒ H =
⋅
− h⎟ ⇒
⎟
ε0 ⎜ C
⎝
⎠
H=
ε
ε0
⎛ ε ⋅ d2
4⋅d⋅λ
⋅ ⎜⎜ 0
−
⎜ C
a 2 − λ2
⎝
⎞
⎟.
⎟⎟
⎠
Resultados Turma
ITA/IME/AFA somente da
unidade CAMPINAS
Como H = n ⋅ e f , temos:
n=
ε
ef ⋅ ε0
⎛ ε ⋅ d2
4⋅d⋅λ
⋅ ⎜⎜ 0
−
⎜ C
a 2 − λ2
⎝
⎞
⎟
⎟⎟
⎠
NOTA: Para que o ângulo θ fosse considerado pequeno deveríamos
h
ter << 2d , o que não necessariamente é verdade.
2
Caso o enunciado colocasse esta condição como verdadeira,
teríamos:
h
λ
4.d.λ
= senθ = tgθ = 2 ⇒ h =
a
2.d
a
Substituindo na equação da associação de capacitores:
2
⎞
ε ⎛ ε0 ⋅ d2
4⋅d⋅λ ⎞
ε ⎛ εo ⋅ d
⎜
⎟⇒
H=
⋅⎜
− h ⎟ ⇒ n ⋅ ef =
−
⎟
ε0 ⎜ C
a ⎟
ε0 ⎜ C
⎝
⎠
⎝
⎠
n=
2006:
•
•
•
•
2
4⋅d⋅λ ⎞
ε ⎛ εo ⋅ d
⎜
⎟
−
e f ⋅ ε0 ⎜ C
a ⎟
⎝
⎠
4 alunos aprovados e classificados na
AFA (além de 2 aprovados e não
classificados), dos 7 que prestaram!
3 alunos aprovados na EPCAr (dos 6 que
prestaram)
4º lugar de SP na EPCAr (3º ano)
... em 2006 é só o começo... venha
ser aprovado você também!
2005:
•
•
•
•
2 alunos aprovados na AFA
1º lugar da UNESP - Matemática
1º lugar da UFSCar - Matemática
80% dos alunos foram aprovados em
Universidades públicas
2004:
•
•
•
•
•
4 alunos aprovados na AFA (dos 5 que
haviam prestado)!
7º lugar de SP na AFA
15º lugar de SP na AFA
1 aprovado no IME
1 aprovado EsPCEx
2003:
•
•
•
•
•
•
7
3º lugar de SP na EsPCEx
1º lugar de SP na EPCAr (3º ano)
12º lugar de SP na AFA
1 aprovado no IME
100% dos alunos foram aprovados na 1ª
fase da Unicamp
80% dos alunos foram aprovados na 2ª
fase da Unicamp