TC 1 UECE - UNIFOR 2013 FASE 1

TC 4
UECE - 2013
FASE 2
SEMANA 10 a 15 de dezembro
MEDICINA
PROF.: Célio Normando
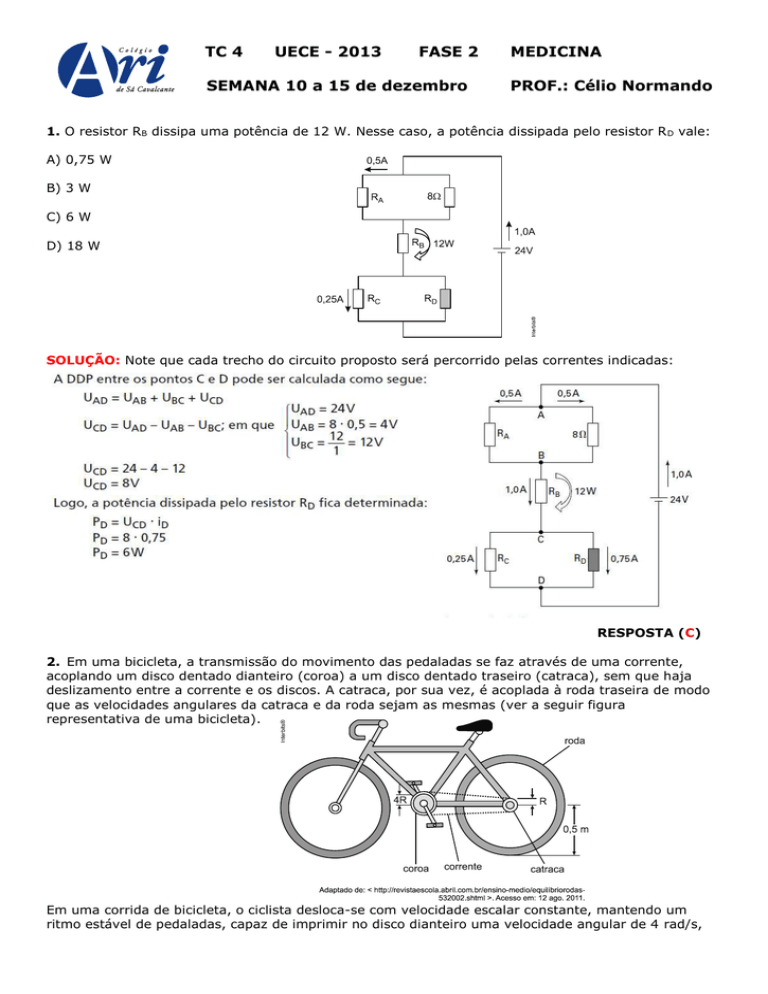
1. O resistor RB dissipa uma potência de 12 W. Nesse caso, a potência dissipada pelo resistor R D vale:
A) 0,75 W
B) 3 W
C) 6 W
D) 18 W
SOLUÇÃO: Note que cada trecho do circuito proposto será percorrido pelas correntes indicadas:
RESPOSTA (C)
2. Em uma bicicleta, a transmissão do movimento das pedaladas se faz através de uma corrente,
acoplando um disco dentado dianteiro (coroa) a um disco dentado traseiro (catraca), sem que haja
deslizamento entre a corrente e os discos. A catraca, por sua vez, é acoplada à roda traseira de modo
que as velocidades angulares da catraca e da roda sejam as mesmas (ver a seguir figura
representativa de uma bicicleta).
Em uma corrida de bicicleta, o ciclista desloca-se com velocidade escalar constante, mantendo um
ritmo estável de pedaladas, capaz de imprimir no disco dianteiro uma velocidade angular de 4 rad/s,
para uma configuração em que o raio da coroa é 4R, o raio da catraca é R e o raio da roda é 0,5 m.
Com base no exposto, conclui-se que a velocidade escalar do ciclista é:
A) 2 m/s
B) 4 m/s
C) 8 m/s
D) 16 m/s
SOLUÇÃO: Dados: ωcor = 4 rad/s; Rcor = 4 R; Rcat = R; Rroda = 0,5 m.
A velocidade tangencial (v) da catraca é igual à da coroa:
v cat  v cor  ωcat Rcat  ωcor Rcor  ωcat R  4  4 R   ωcat  16 rad / s.
A velocidade angular ( ω ) da roda é igual à da catraca:
ωroda  ωcat

vroda
 ωcat
Rroda

vroda
 16  v roda  8 m / s 
0,5
RESPOSTA (C)
vbic  vroda  8 m / s.
3. No circuito RC, mostrado abaixo, a chave Ch está aberta. Inicialmente o capacitor está carregado e
sua ddp é VC  22 V . A chave Ch é fechada e uma corrente elétrica começa a circular pelo circuito.
A intensidade da corrente elétrica inicial que circula no resistor, em ampères, vale:
A) 5A
B) 11A
C) 6A
D) 17A
SOLUÇÃO: De acordo com a segunda lei de Kirchhoff, teremos:
VC  VR  ε  0  22  VR  12  0
VR  10V
Aplicando a definição de resistência elétrica:
R
VR
10
2
i
i
i  5A
TEXTO PARA AS QUESTÕES 4 e 5.
O tempo de reação tR de um condutor de um automóvel é definido como o
intervalo de tempo decorrido entre o instante em que o condutor se depara
com urna situação de perigo e o instante em que ele aciona os freios.
(Considere dR e dF, respectivamente, as distâncias percorridas pelo veículo
durante o tempo de reação e de frenagem; e dT, a distância total percorrida.
Então, dT = dR + dF).
Um carro trafega com velocidade constante de módulo v = 54,0 km/h
em uma pista horizontal. Em dado instante, o condutor visualiza uma
situação de perigo, e seu tempo de reação a essa situação é de 4/5 s, como
ilustrado na sequência de figuras.
RESPOSTA (A)
4. Considerando-se que a velocidade do carro permaneceu inalterada durante o tempo de reação tR, é
correto afirmar que a distância dR é de
A) 3,0 m.
B) 12,0 m.
C) 43,2 m.
D) 60,0 m.
SOLUÇÃO: Convertendo a velocidade para unidades SI:
vM  54 3,6  15 m s
Sendo o tempo de reação igual a  4 5  s, temos:
4
 34
5
dR  12 m
dR  15 
RESPOSTA (B)
5. Em comparação com as distâncias dR e dF, já calculadas, e lembrando que dT = dR + dF, considere as
seguintes afirmações sobre as distâncias percorridas pelo carro, agora com o dobro da velocidade
inicial, isto é, 108 km/h.
I. A distância percorrida pelo carro durante o tempo de reação do condutor é de 2dR.
II. A distância percorrida pelo carro durante a frenagem é de 2dF.
III. A distância total percorrida pelo carro é de 2dT.
Quais estão corretas?
A) Apenas I.
B) Apenas II.
C) Apenas I e II.
D) Apenas I e III.
SOLUÇÃO: I. Convertendo a velocidade para unidades SI:
vM  108 3,6  30 m s
Sendo o tempo de reação igual a  4 5  s, temos:
4
 64
5
 24 m
dR2  30 
dR2
 dR2  2dR (Verdadeiro)
II. Utilizando a equação de Torricelli, temos:
v 2  v 02  2a ΔS
02  302  2( 7,5)dF2
15 dF2  900
dF2  60 m
 dF2  4dF (Falso)
III. A distância total dR percorrida no primeiro caso:
dT  dR  dF
dT  12  15
dT  27 m
A distância total dR2 percorrida no segundo caso:
dT2  dR2  dF2
dT2  24  60
dT2  84 m (Falso)
RESPOSTA (A)
6. Outro exemplo de desenvolvimento, com vistas a recargas rápidas, é o protótipo de uma bateria de
íon-lítio, com estrutura tridimensional. Considere que uma bateria, inicialmente descarregada, é
carregada com uma corrente média im  3,2 A até atingir sua carga máxima de Q = 0,8 Ah . O tempo
gasto para carregar a bateria é de:
A) 240 minutos.
B) 90 minutos.
C) 15 minutos.
D) 4 minutos.
SOLUÇÃO: Da definição de corrente elétrica:
Q
Q 0,8 Ah
im 
 t  
 0,25 h  0,25  60 min  
t
im
3,2 A
t  15 min.
RESPOSTA (C)
7. Um móbile pendurado no teto tem três elefantezinhos presos um ao outro por fios, como mostra a
figura. As massas dos elefantes de cima, do meio e de baixo são, respectivamente, 20g, 30g e 70g. Os
valores de tensão, em newtons, nos fios superior, médio e inferior são, respectivamente, iguais a:
Note e adote: Desconsidere as massas dos fios.
Aceleração da gravidade g  10 m/s2 .
A) 1,2; 1,0; 0,7.
B) 1,2; 0,5; 0,2.
C) 0,7; 0,3; 0,2.
D) 0,2; 0,5; 1,2.
SOLUÇÃO: Analisemos o diagrama de forças sobre cada móbile.
Dados: mc = 20 g = 2010–3 kg; mm = 30 g = 3010–3 kg; mb = 70 g = 7010–3 kg; g = 10 m/s2.
De Cima (C)
Do Meio (M)
De Baixo (B)
Como se trata de um sistema em equilíbrio, a resultante das forças em cada elefante é nula. Assim:
(C)  TS  PC  TM  0

(M)  TM  PM  TB  0
(B)  T  P  0
B
B

+
 TS  PC  PM  PB  0  TS  PC  PM  PB
TS   20  30  70   10 3   10  TS  120  10 2
TS  1,2 N.


Em (B):
TB  PB  0  TB  PB  70  103  10 
TB  0,7 N.
Em (M):
TM  PM  TB  0  TM  PB  TB  30  70   103   10 
TB  1,0 N.
RESPOSTA (A)
8. Dentro do tubo de imagem de um televisor, a corrente elétrica, numa bobina, aplica sobre um
elétron passante um campo magnético de 5  104 T, de direção perpendicular à direção da velocidade
do elétron, o qual recebe uma força magnética de 1 1014 N. Qual o módulo da velocidade desse
elétron? (Considere o módulo da carga do elétron como 1,6  1019 C. )
A) 1,60  105 m s
B) 7,60  106 m s
C) 4,33  107 m s
D) 1,25  108 m s
SOLUÇÃO: Dados: B = 5  10–4 T; q = 1,6  10–19 C; F = 1  10–14 N; θ = 90°.
Da expressão da força magnética:
F | q | v B senθ  v 
F
1,4  1014

q B sen90 1,6  1019  5  104

F  1,25  108 m / s.
RESPOSTA (D)
9. Uma pessoa, de massa 80,0 kg, consegue aplicar uma força de tração máxima de 800,0 N. Um
corpo de massa M necessita ser levantado como indicado na figura a seguir. O coeficiente de atrito
estático entre a sola do sapato da pessoa e o chão de concreto é  e  1,0 .
A maior massa M que pode ser levantada pela pessoa sem que esta deslize, para um ângulo   45º .
A) 20 kg
B) 20 2 kg
C) 40 kg
D) 40 2 kg
SOLUÇÃO: Esboço das forças que atuam no sistema:
Condição da questão:
Tmax  800N
P '  T  M.g  T  M.10  800
Mmax  80kg
Para que a pessoa levante a caixa sem deslizar, temos:
Na pessoa: A  T.cosθ
Na caixa: T  P'  M.g
Ou seja, A  T.cos θ  A  P'.cos θ  A  M.g.cos θ (EQUAÇÃO 1)
Força de atrito que atua na pessoa: A  μ.N
Como: N  T.senθ  P  N  P  T.senθ  N  m.g  T.senθ
Teremos: A  μ.N  μ.(m.g  T.senθ)
Substituindo na equação 1:
A  M.g.cos θ  μ.(m.g  T.senθ)  M.g.cos θ
Lembre-se que: T  P'  M.g
Ou seja: μ.(m.g  T.senθ)  M.g.cos θ  μ.(m.g  M.g.senθ)  M.g.cos θ
Substituindo os valores determinaremos o maior valor da massa (M) da caixa que a pessoa pode
levantar sem deslizar
2
2
μ.(m.g  M.g.senθ)  M.g.cos θ  1.(80.10  M.10.sen45º )  M.10.cos 45º  800  M.10
 M.10.
2
2
RESPOSTA (D)
M  40 2kg
10. Um disjuntor é um dispositivo eletromecânico destinado a proteger circuitos contra a sobrecarga e
o superaquecimento. Pretende-se dimensionar um disjuntor para proteger um ambiente cuja rede
elétrica fornece uma tensão de 120 V e possui uma lâmpada de 60 W, um ar condicionado de 1000 W
e um computador de 140 W. Este ambiente ficará mais bem protegido, considerando-se a tolerância
de 30%, com um disjuntor de:
A) 30 A
B) 22 A
C) 20 A
D) 13 A
SOLUÇÃO: Dados: U = 120 V; PL = 60 W; Par = 1000 W; Pcomp = 140 W; Imáx = 1,3 i.
P  U i  60  1.000  140  120 i  1.200  120 i  i  10 A.
Imáx  1,3 i  1,3 10 
 Imáx  13 A.
RESPOSTA (D)
11. Em um trecho retilíneo de estrada, dois veículos, A e B, mantêm velocidades constantes
VA  14 m/s e VB  54 km/h .
Sobre os movimentos desses veículos, pode-se
afirmar que:
A) mantidas essas velocidades, A não conseguirá
ultrapassar B.
B) A está mais rápido do que B.
C) a cada segundo que passa, A fica dois metros
mais distante de B.
D) depois de 40 s A terá ultrapassado B.
SOLUÇÃO: Dados: VA = 14 m/s; VB = 54 km/h = 15 m/s.
Como a velocidade de A é menor que a de B, A não conseguirá ultrapassar B.
RESPOSTA (A)
12. Um estudante do ensino médio quer montar em seu quarto um circuito com quatro lâmpadas
idênticas com a seguinte especificação (2,0 V – 8,0 W). Mas para alimentar o circuito ele conta
somente com uma fonte (ε  20,0 V e r  1,0 ). Para não queimar as lâmpadas ele usa um resistor R,
como está indicado na figura abaixo:
Com base na situação exposta, é CORRETO afirmar que:
A) as lâmpadas vão queimar, independentemente do valor de R.
B) a resistência R vale 2,0 .
C) o objetivo do resistor R neste circuito é transformar energia
elétrica em energia luminosa.
D) se o estudante associar as lâmpadas em paralelo, elas
não vão queimar.
SOLUÇÃO: Dados: UL = 2 V; PL = 8 W; ε = 20 V e r = 1 .
Como as lâmpadas estão em série, a tensão na associação de lâmpadas é a soma das tensões
individuais:
Uassic  4  2  8 V.
Calculando a corrente no circuito:
PL  UL i  8  2 i  i  4 A.
Calculando a resistência de cada lâmpada:
UL  RL i  2  RL 4  RL  0,5 .
Aplicando a lei das malhas ao circuito:
ε  Req i  ε  r  Rassoc  R  i  20  1  4 0,5   R  4  5  3  R 
R  2 .
RESPOSTA (B)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
PUC-SP 2012
UFPB 2012
UFPE 2012
UFRS 2012
UFRS 2012
UNICAMP 2012
FUVEST 2012
UCS 2012
UEL 2012
IFBA 2012
IFSP 2012
IFSC 2012