ET2N-3 - Gabarito

Curso de Engenharia de Petróleo
Disciplina:
Nota:
Professor: Rudson Ribeiro Alves
Rubrica
Coordenador
Aluno:
Turma: ET2N
Semestre: 1 sem/2014
Data: 29/05/2014
Avaliação: 3a Prova
Valor: 10,0 ptos
INSTRUÇÕES DA PROVA:
•
•
•
•
•
Leia atentamente as questões antes de respondê-las;
Todas as questões devem ser feitas com caneta Azul;
Provas feitas a lápis, com uso de corretivos ou repassadas a caneta por sobre execução a lápis serão tratadas como
feitas a lápis;
Não é permitido o empréstimo de qualquer material durante a prova;
Somente é permitido o uso de calculadora científica simples (como as Casio fx82), para a realização dos cálculos,
qualquer outro equipamento eletrônico é proibido.
F (N)
Questão 1.
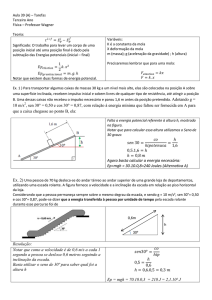
O gráfico ao lado representa a força resultante atuando
sobre um bloco de 1,20 kg, enquanto que este desliza sobre
uma superfície ao longo de um eixo fixo. Sendo a
velocidade do bloco igual a 9,00 m/s, ao atingir a posição
8,00 m, determine o trabalho realizado sobre este nos
intervalos:
m=1,20 kg
v 8=9,00 m /s
20
10
0
0,0
2,0
4,0
6,0
8,0 x (m)
-10
(a) 0 a 3,00 m;
W F =área sob a curva F× x
W 03=W 01+W 13=
(10+20).1 20.2
+
=15+20=35 J
2
2
(b) 3,00 a 6,00 m.
W 36=0
(c) Qual a potência aplicada sobre o bloco quando este passa pela posição 8,00 m?
P 8= F 8⋅v 8 =F 8 . v 8 . cos(180° )=10.9 .(−1)=−90 W
Boa Prova
N
x
F = 13,0N
f = 5,00N
30°
Questão 2.
Na figura ao lado são apresentadas as forças que atuam sobre
uma caixa de 800 g que se move ao longo do eixo-x.
m=800 g=0,800 kg
(a) Determine o trabalho que cada força realiza sobre a caixa
quando esta é deslocada por 2,50 m rampa abaixo?
25°
P
W f =f⋅d=f .d . cos(180° )=5⋅2,5⋅(−1)=−12,5 J
W N = N⋅d= N . d . cos(90 °)=0
W F =F⋅d= F . d .cos(30 °)=13⋅2,5⋅(0,5)=28,1 J
W P= P⋅d= P . d. cos(90 °−25 °)=0,8⋅9,8⋅2,5⋅cos(65 ° )=8,28 J
(b) Se a caixa estiver inicialmente parada, qual a sua velocidade após o deslocamento?
W if =∑ W F =Δ K
i
1
2 1
2 com
W f +W N +W F +W P= m v − m v 0
v 0 =0
2
2
2
23,88=0,8 v
v=7,73 m/s
Boa Prova
Uma mola de constante elástica 1960 N/m* é usado para lançar uma esfera de
1,00 kg, verticalmente para cima conforme ilustra a figura ao lado.
h
5,96mm
Questão 3.
k=1960 N / m
m=1,00 kg
(a) Se a mola for comprimida de 5,00 cm, a que altura “h”, acima desta, a esfera foi
lançada?
x0
k
x0 =5,00 cm= 0,0500 m
A energia inicial:
1
2
Ei =U ei= k x0 =2,45 J
2
Ef =U Gf =mg .(h +x0 )=9,8 h+0,49 , com zero gravitacional na mola comprimida.
Ei = Ef
2,45=9,8h+0,49
h=0,20 m=20 cm
Obs: a constante elástica estava errada, deveria ter sido de 1960 N/m. Está valendo a
montagem da questão, energia inicial e final.
(b) Qual a velocidade da esfera ao deixar a mola?
1
2
2
Ef '=U Gf +K f =mg . x 0 + m v =0,49 +0,5 v
2
Ei = Ef '
0,49+0,5v 2=2,45
v=1,98 m/s
Obs: este resultado também fica comprometido com a mudança do valor de k!
*
A constante elástica da Questão 03 esta errada. O valor adequado é 1960 N/m.
Boa Prova
Questão 4.
Duas molas de constante elástica k = 200 N/m são dispostas nos extremos de uma superfície
de comprimento L = 50 cm, com coeficiente de atrito igual a 0,25. Inicialmente a mola da
esquerda é comprimida de 5,0 cm e usada para lançar um bloco de 150 g.
k=200 N /m
L=50 cm=0,50 m
μ=0,25
m=150 g=0,150kg
x0 =5,0 cm=0,05 m
k m
A
k
L
35,74mm
(a) Qual a primeira compressão da mola à direita da superfície?
1
2
Ei =U ei= k x0 =0,250 J
2
1 2
2
Ef = k x =100 x
2
W f =−f⋅L=μ N L=−μ mgL=−0,18375 J
Fazendo a conservação:
Ef = E i +W f
100 x 2=0,250−0,18375
x=0,0257 m=2,57 cm
(b) A que distância à esquerda do ponto A, o bloco parará?
Para resolver esta questão, considere uma superfície infinita com coeficiente de atrito 0,25 à
frente da mola à direita. Com isto, resolva o problema até o corpo parar:
Ef =0 , o corpo para!
O trabalho da força de atrito fica:
W f =−f⋅S =μ N S=−0,3675S
Fazendo a conservação:
Ef = E i +W f
0=0,250−0,3675⋅S
S=0,680m=68,0 cm
como L é 50 cm, o bloco parará a 18 cm à esquerda do ponto A.
Boa Prova