Vantagens do Sistema Trifásico

Vantagens do Sistema Trifásico
Original: 26-06-2013
Homero Sette
Revisão: 30-06-2013
Agora que o sistema trifásico chegou aos amplificadores, com o advento do TRI – 6000 S da Etelj, o
interesse pelo assunto na comunidade de áudio aumentou muito e, por esse, motivo voltamos ao tema.
A maior parte da energia elétrica distribuída no mundo é feita sob a forma de sistemas trifásicos.
Esse fato não é por acaso, pois o sistema trifásico realmente oferece significativas vantagens em relação ao
monofásico, conforme podemos ver abaixo:
 O sistema trifásico usa menor quantidade de cobre ou alumínio para entregar a mesma potência que um
sistema monofásico equivalente;
 Geradores trifásicos são menores e mais leves que seus equivalentes monofásicos por usarem com maior
eficiência seus enrolamentos. Isso se verifica inclusive nos automóveis, cujos alternadores produzem energia
trifásica alternada, que é posteriormente transforma em continua, através de retificadores;
 Um motor trifásico é menor que seu correspondente monofásico de mesma potência;
 Motores trifásicos, devido ao campo girante produzido pelas três fases, partem sem a necessidade de
dispositivos especiais. Já o campo pulsante dos motores monofásicos exige um enrolamento extra de partida;
 Motores trifásicos produzem um torque constante, o que não é possível nos motores monofásicos;
 Devido ao torque constante os motores trifásicos são menos sujeitos a vibrações;
 Retificadores trifásicos apresentam menos ondulação na tensão retificada (ripple) que os monofásicos;
 A potência total em um sistema trifásico nunca é nula. No sistema monofásico anula-se sempre que a
tensão ou a corrente passam pelo zero (os motores monofásicos só continuam girando graças à inércia);
 A potência instantânea total, em um sistema trifásico equilibrado é constante, ou seja, não varia no tempo.
Esta última propriedade é extremamente importante e surpreendente, residindo nela a superioridade do
desempenho de muitos dispositivos trifásicos, e merece ser analisada em detalhe.
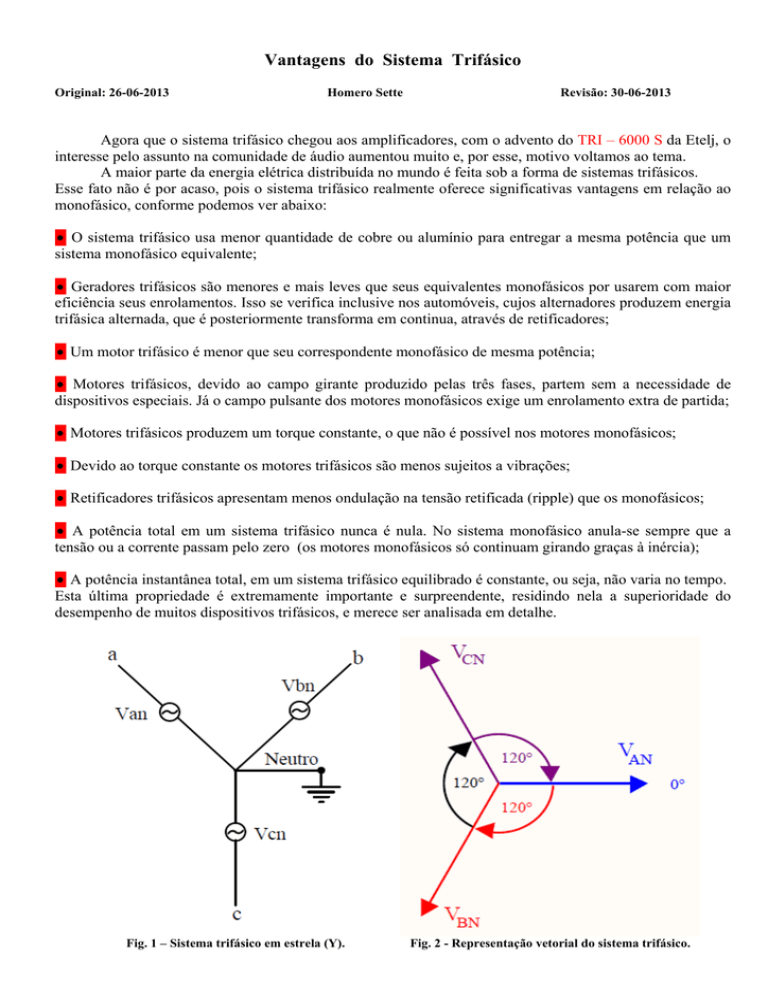
Fig. 1 – Sistema trifásico em estrela (Y).
Fig. 2 - Representação vetorial do sistema trifásico.
Potência em Sistema Monofásico
Utilizando a tensão VAN , entre fase e neutro, do sistema mostrado nas Figs. 1 e 6, representaremos
uma tensão monofásica, por exemplo 127 Volts eficazes, também denominada RMS, ou seja, 127 VRMS.

VAN  VAN  0 o 
2  E EF  0 o
(representação fasorial da tensão, onde VAN é o valor de pico)
2  E EF  sen   t 
v AN 
(tensão instantânea senoidal, aplicada na carga)

ZL  ZL    ZL  cos     j  sen     (representação polar e cartesiana da impedância de carga)


VAN
IAN   
ZL
2  E EF  0 o

ZL  
2
E EF
 o 
ZL
2  I EF  sen   t   
i AN 
2  I EF    o (representação fasorial da corrente)
(corrente instantânea senoidal, na carga)
p AN  v AN  i AN   2  E EF  sen   t     2  I EF  sen   t    
(potência instantânea)
p AN  v AN  i AN  2  E EF  I EF  sen   t    sen   t    
a   t
;
b   t  
sen  a   sen  b  
;
ab  
;
a  b  2   t  
cos  a  b 
cos  a  b 

2
2
(identidade trigonométrica)
cos  2   t    
 cos   

p AN  v AN  i AN  2  E EF  I EF  

2
 2

p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos  2   t   
A potência instantânea acima pode ser decomposta em suas componentes:
E EF  I EF
Potência Aparente, medida em Volt  Ampere, (VA);
cos   
Fator de Potência (adimensional);
E EF  I EF  cos   
Potência Real (média, consumida), em Watts, erroneamente chamada de potência eficaz;
 E EF  I EF  cos  2   t   
Componente cossenoidal da potência, com valor médio nulo, defasada de
180 o e com o dobro da freqüência das ondas de corrente e tensão. Responsável pela entrega de uma energia
“pulsante”.
E I
E I
P
Como E EF  I EF  P  P  P P  P , podemos expressar a potência média como metade da potência
2
2
2 2
de pico vezes o fator de potência:
PME  E EF  I EF  cos    
PP
 cos   
2
Tensão, Corrente e Potência Entre Fase e Neutro
1.5
1.4
1.3
1.2
1.1
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
-0.8
-0.9
-1
-1.1
-1.2
-1.3
-1.4
-1.5
van
pan
ian
P ME
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Tempos em milissegundos
Tensão, Corrente e Potência Entre Fase e Neutro
Fig. 3 - Tensão, corrente, potência instantânea e potência média em circuito monofásico com carga puramente resistiva.
1.5
1.4
1.3
1.2
1.1
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
-0.8
-0.9
-1
-1.1
-1.2
-1.3
-1.4
-1.5
van
pan
ian
P ME
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Tempos em milissegundos
Tensão, Corrente e Potência Entre Fase e Neutro
Fig. 4 - Tensão, corrente, potência instantânea e potência média em circuito monofásico com carga puramente indutiva.
1.5
1.4
1.3
1.2
1.1
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
-0.8
-0.9
-1
-1.1
-1.2
-1.3
-1.4
-1.5
van
pan
ian
P ME
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Tempos em milissegundos
Fig. 5 - Tensão, corrente, potência instantânea e potência média em circuito monofásico com carga RL.
16
Exemplo 1:

Para f = 60 Hz (16,7 ms de período) , E EF  1 V e ZL  2  0 o (carga puramente resistiva), temos:
I EF  1V / 2   0, 5 A e PME  E EF  I EF  cos     1  0,5  cos  0   1  0,5 1  0,5 Watt.
Na Fig. 3 a curva vermelha representa a tensão instantânea v AN 
A curva azul corresponde à corrente instantânea i AN 
2 1 sen  377  t  ;
2  0,5  sen  377  t  0 o   0, 707  sen  377  t  ;
A curva rosa é a potência instantânea, resultante do produto entre a onda de tensão e a de corrente, dada por
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos  2   t    onde E EF  I EF  cos    é a potência média,
também chamada de potência ativa ou real.
Como a carga é uma resistência pura, a defasagem é nula e a tensão e a corrente passam pelo zero nos
mesmos instantes de tempo, ou seja, a tensão e a corrente estão em fase.
Exemplo 2:

Para f = 60 Hz (16,7 ms de período) , E EF  1 V e ZL  2  90 o  j  2 (carga puramente indutiva).
A indutância de carga será igual a 2  2    f  L  L  2 / 2    f  2 / 377  0, 0053 H  5,3 mH
Na prática não se consegue uma indutância pura, ou seja, sem certa resistência em série, própria do fio.
Neste exemplo, com uma resistência igual ou menor que 0,2 Ohms estaremos muito próximos do caso ideal.
I EF  1V / 2   0, 5 A e PME  E EF  I EF  cos     1  0,5  cos  90   1  0,5  0  0 Watt, ou seja, a
potência média é nula por uma simples razão: a reatância indutiva não dissipa potência
Na Fig. 4 a curva vermelha representa a tensão instantânea v AN  2 1 sen  377  t  e a curva azul corresponde à corrente instantânea i AN 
2  0,5  sen  377  t  90 o   0, 707  sen  377  t  90 o  , onde vemos
que a corrente está 90 o atrasada em relação à tensão (em uma capacitância estaria adiantada de 90 o );
A curva rosa é a potência instantânea, resultante do produto entre as ondas de tensão e corrente, dada por
p AN  v AN  i AN   E EF  I EF  cos  2   t  90 o    E EF  I EF  s en  2   t  , uma vez que a potência média
é nula, representando esta equação uma onda senoidal, invertida (defasada de 180 o ), com o dobro da
freqüência da tensão e da corrente.
Exemplo 3:
Para f = 60 Hz (16,7 ms de período) , E EF  1 V , sendo a carga composta, em partes iguais, de resistência e

2
2
 j 2 
 2  j 2 .
indutância, dada por ZL  2  45 o  2  cos  45 o   j  2  s en  45 o   2 
2
2
A componente resistiva da carga será uma resistência de 2 Ohms enquanto que a componente indutiva
corresponderá a 2  2    f  L  L  2 / 2    f  2 / 377  0, 00375 H  3, 75 mH .
I EF  1V / 2   0, 5 A e PME  E EF  I EF  cos     1 0,5  cos  45   1  0,5  2 / 2  0,354 Watt, e que
é toda ela dissipada no resistor, uma vez que a reatância indutiva não dissipa potência.
Na Fig. 5 a curva vermelha representa a tensão instantânea v AN  2 1 sen  377  t  e a curva azul
corresponde à corrente instantânea i AN 
2  0,5  sen  377  t  45 o   0, 707  sen  377  t  45 o  onde
vemos que a corrente está 45 o atrasada em relação à tensão;
A curva rosa é a potência instantânea, resultante do produto entre as ondas de tensão e corrente, dada por
2
p AN  v AN  i AN  E EF  I EF  cos  45 o   E EF  I EF  cos  2   t  45 o  e E EF  I EF  cos  45 o   1 0,5 
 0,354
2
p AN  0,354  0,5  cos  2   t  45 o   0,354  0,5  cos  377  t  45 o  onde 0,354 W a potência média.
Conforme os exemplos acima a potência instantânea entre fase e neutro, de um sistema trifásico, ou
seja, em uma única fase (monofásico) é uma onda cossenoidal, com o dobro da freqüência, superposta a uma
componente constante, que é a potência média. Assim a potência instantânea é variável, passando pelo zero.
Potência Instantânea em Função das Potências Ativa e Reativa
A potência instantânea monofásica, obtida anteriormente, e dada pela equação abaixo, pode ser
visualizada em função das potências ativa e reativa, conforme abaixo:
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos  2   t   
cos  a  b   cos  a   cos  b   s en  a   s en  b 
(identidade trigonométrica)
Fazendo a  2   t e b   , vem:
cos  2   t     cos  2   t   cos     s en  2   t   s en   
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos  2   t   
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF   cos  2   t   cos     s en  2   t   s en    
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos     cos  2   t   E EF  I EF  s en     s en  2   t 
p AN  v AN  i AN  E EF  I EF  cos     1  cos  2   t    E EF  I EF  s en     s en  2   t 
p AN  v AN  i AN  P  1  cos  2   t    Q  s en  2   t  onde:
P  E EF  I EF  cos    é a potência ativa ou real, em Watts, consumida pelo circuito, sendo sempre positiva
ou nula, caso o fator de potência, cos    , seja zero (cargas puramente indutivas ou puramente capacitivas).
P  1  cos  2   t   também é sempre positiva, com valor médio igual a P, e varia no tempo, representando a variação da potência fornecida por um circuito monofásico. A média de p AN é igual a P.
Q  E EF  I EF  sen    é a potência reativa, em V  A , que flutua entre o gerador e a carga: quando positiva é
fornecida pelo gerador para a carga e quando negativa é devolvida da carga para o gerador. Quando   0 o
(circuito puramente resistivo), Q = 0.
Potência Instantânea Total no Sistema Trifásico Balanceado
Fig. 6 – Ligação monofásica.
Fig. 7 – Ligação Trifásica.
No caso anterior foi analisada a situação da energia sendo entregue a uma carga monofásica (Fig. 6).
Agora vamos enfocar a situação onde a energia é entregue a uma carga trifásica, equilibrada, conforme
mostra a Fig. 7.
Tensões Entre Fases e Neutro
Fasorial

VAN  2  E EF  0 o
;

VBN 

; VCN 
2  E EF  120 o
Instantâneo
v AN  2  E EF  sen   t  ; v BN 
2  E EF  sen   t  120 o  ; v CN 
2  E EF  120 o
2  E EF  sen   t  120 o 
Impedância de Carga

ZL  ZL    ZL  cos     j  sen    
Correntes nas Cargas
Fasorial


VAN
IAN   
ZL
2  E EF  0 o

ZL  


VBN
IBN   
ZL
2  E EF  120 o

ZL  


VCN
ICN   
ZL
2  E EF  120 o

ZL  
2
E EF
 o 
ZL
2
2
2  I EF    o
E EF
   o  120 o 
ZL
E EF
   o  120 o 
ZL
2  I EF    o  120 o
2  I EF    o  120 o
Instantâneo
i AN 
i BN 
i CN 
2  I EF  sen   t   
2  I EF  sen   t    120 o 
2  I EF  sen   t    120 o 
Potências Instantâneas no Sistema Trifásico Equilibrado
Potência Instantânea p AN
p AN  v AN  i AN   2  E EF  sen   t     2  I EF  sen   t    
p AN  v AN  i AN  2  E EF  I EF  sen   t    sen   t    
x   t
;
y   t  
sen  x   sen  y  
;
xy  
;
x  y  2   t  
cos  x  y   cos  x  y 
cos     cos  2   t   

2
2
p AN  v AN  i AN  2  E EF  I EF 
cos     cos  2   t   
2
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos  2   t   
Potência Instantânea p BN
p BN  v BN  i BN   2  E EF  sen   t  120 o     2  I EF  sen   t    120 o  
p BN  v BN  i BN  2  E EF  I EF  sen   t  120 o    sen   t    120 o  
x   t  120 o
;
y   t    120 o
;
xy  
;
x  y  2   t    240 o
cos     cos  2   t    240 o 
cos  x  y   cos  x  y 
sen  x   sen  y  

2
2
p BN  v BN  i BN  2  E EF  I EF 
cos     cos  2   t    240 o 
2
p BN  v BN  i BN  E EF  I EF  cos     E EF  I EF  cos  2   t    240 o 
Potência Instantânea pCN
pCN  vCN  i CN   2  E EF  sen   t  120 o     2  IEF  sen   t    120 o  
pCN  vCN  i CN  2  E EF  I EF  sen   t  120 o    sen   t    120 o  
x   t  120 o
;
y   t    120 o
;
xy  
;
x  y  2   t    240 o
cos     cos  2   t    240 o 
cos  x  y   cos  x  y 
sen  x   sen  y  

2
2
pCN  v CN  i CN  2  E EF  I EF 
pCN  vCN  i CN
cos     cos  2   t    240 o 
2
 E EF  I EF  cos     E EF  I EF  cos  2   t    240 o 
Potência Instantânea Total
p T  p AN  p BN  p CN
p T  E EF  I EF  cos     E EF  I EF  cos  2   t     ...
E EF  I EF  cos     E EF  I EF  cos  2   t    240 o   ...
E EF  I EF  cos     E EF  I EF  cos  2   t    240 o 




p T  3  E EF  I EF  cos     E EF  I EF   cos  2   t     cos 2   t    240 o  cos 2   t    240 o 
Fazendo: 2   t    x , temos:
2   t    240 o  x  240 o e 2   t    240 o  x  240 o de modo que
cos  2   t     cos  2   t    240 o   cos  2   t    240 o   cos  x   cos  x  240 o   cos  x  240 o 
Utilizando as identidades trigonométricas abaixo:
cos  a  b   cos  a   cos  b   s en  a   s en  b 
cos  a  b   cos  a   cos  b   s en  a   s en  b 
cos  a  b   cos  a  b   2  cos  a   cos  b 
para a = x e b = 240 o , vem:
 1
cos  a  b   cos  a  b   2  cos  a   cos  b   2  cos  x   cos  240 o   2  cos  x        cos  x 
 2
cos  x   cos  x  240 o   cos  x  240 o   cos  x   cos  x   0




cos  2   t     cos 2   t    240 o  cos 2   t    240 o  0
E EF  I EF  cos  2   t     cos  2   t    240 o   cos  2   t    240 o    E EF  I EF  0  0
p T  3  E EF  I EF  cos    - 0
p T  3  E EF  I EF  cos   
O desenvolvimento acima mostrou que a potência instantânea total, entregue às cargas de um sistema
trifásico balanceado é constante, ou seja, em qualquer instante de tempo o sistema recebe sempre a mesma
potência. Essa propriedade é muito importante e explica a superioridade do sistema trifásico em muitas
aplicações.
Potências Instantâneas em Função das Potências Ativa e Reativa
As potências instantâneas, obtidas anteriormente, podem ser desenvolvidas em função das potências
ativa e reativa, conforme abaixo, levando ao mesmo resultado.
Potência Instantânea p AN
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos  2   t   
cos  a  b   cos  a   cos  b   s en  a   s en  b 
(identidade trigonométrica)
Fazendo a  2   t e b   , vem:
cos  2   t     cos  2   t   cos     s en  2   t   s en   
Potências Instantâneas e Total Entre Fase e Neutro
1.6
1.4
pan
pbn
1.2
pc n
pTn
1
0.8
0.6
0.4
0.2
0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Tempos em milissegundos
Fig. 8 - Potências nas cargas e potência total em circuito trifásico equilibrado com carga puramente resistiva.
0.5
Potências Instantâneas e Total Entre Fase e Neutro
0.4
pan
0.3
pbn
pcn
0.2
pTn
0.1
0
-0.1
-0.2
-0.3
-0.4
-0.5
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Tempos em milissegundos
Fig. 9 - Potências nas cargas e potência total em circuito trifásico equilibrado com carga puramente indutiva.
1.2
Potências Instantâneas e Total Entre Fase e Neutro
pan
pbn
1
pc n
pTn
0.8
0.6
0.4
0.2
0
-0.2
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Tempos em milissegundos
Fig. 10 - Potências nas cargas e potência total em circuito trifásico equilibrado com carga RL.
16
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos  2   t   
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos  2   t   cos     s en  2   t   s en    
p AN  v AN  i AN  E EF  I EF  cos     E EF  I EF  cos     cos  2   t   E EF  I EF  s en     s en  2   t 
p AN  v AN  i AN  E EF  I EF  cos     1  cos  2   t    E EF  I EF  s en     s en  2   t 
p AN  v AN  i AN  P  1  cos  2   t    Q  s en  2   t 
Potência Instantânea p BN
p BN  v BN  i BN  E EF  I EF  cos     E EF  I EF  cos  2   t    240 o 
cos  a  b   cos  a   cos  b   s en  a   s en  b 
(identidade trigonométrica)
Fazendo a  2   t   e b  240 o , vem:
cos  2   t     240 o   cos  2   t     cos  240 o   s en  2   t     s en  240 o 

3
 1
cos  2   t     240 o   cos  2   t         s en  2   t      

 2
 2 
1
3
 s en  2   t   
cos  2   t     240 o     cos  2   t    
2
2
 1

3
p BN  v BN  i BN  E EF  I EF  cos     E EF  I EF     cos  2   t    
 s en  2   t    
2
 2

1
3
p BN  v BN  i BN  E EF  I EF  cos     E EF  I EF   cos  2   t     E EF  I EF 
 s en  2   t   
2
2
cos  a  b   cos  a   cos  b   s en  a   s en  b 
cos  2   t     cos  2   t   cos     s en  2   t   s en   
1
1
E EF  I EF   cos  2   t     E EF  I EF   cos  2   t   cos     s en  2   t   s en    
2
2
sen  a  b   sen  a   cos  b   sen  b   cos  a 
s en  2   t     sen  2   t   cos     sen     cos  2   t 
E EF  I EF 
3
3
3
 s en  2   t     E EF  I EF 
 sen  2   t   cos     E EF  I EF 
 sen     cos  2   t 
2
2
2
1
3
p BN  v BN  i BN  E EF  I EF  cos     E EF  I EF   cos  2   t     E EF  I EF 
 s en  2   t   
2
2
1
1
p BN  v BN  i BN  E EF  I EF  cos     E EF  I EF   cos  2   t   cos     E EF  I EF   s en  2   t   s en     ...
2
2
3
3
 E EF  I EF 
 sen  2   t   cos     E EF  I EF 
 sen     cos  2   t 
2
2
1
1
p BN  v BN  i BN  E EF  I EF  cos     E EF  I EF   cos     cos  2   t   E EF  I EF   s en     s en  2   t   ...
2
2
3
3
 E EF  I EF 
 cos     sen  2   t   E EF  I EF 
 sen     cos  2   t 
2
2
1
1


p BN  v BN  i BN  E EF  I EF  cos     1   cos  2   t    E EF  I EF  s en      s en  2   t   ...
2
2


 E EF  I EF  cos    
3
3
 sen  2   t   E EF  I EF  sen    
 cos  2   t 
2
2
1
1
3
3


p BN  v BN  i BN  P  1   cos  2   t    Q   s en  2   t   P 
 sen  2   t   Q 
 cos  2   t 
2
2
2
2


Q
1
3
3


p BN  v BN  i BN  P  1   cos  2   t      P 
 cos  2   t 
  sen  2   t   Q 
2
2
2
2




Potência Instantânea pCN
pCN  vCN  i CN  E EF  I EF  cos     E EF  I EF  cos  2   t    240 o 
cos  a  b   cos  a   cos  b   s en  a   s en  b 
(identidade trigonométrica)
Fazendo a  2   t   e b  240 o , vem:
cos  2   t     240 o   cos  2   t     cos  240 o   s en  2   t     s en  240 o 

3
 1
cos  2   t     240 o   cos  2   t         s en  2   t      

 2
 2 
1
3
cos  2   t     240 o     cos  2   t    
 s en  2   t   
2
2
pCN  vCN  i CN  E EF  I EF  cos     E EF  I EF  cos  2   t    240 o 
 1

3
pCN  vCN  i CN  E EF  I EF  cos     E EF  I EF     cos  2   t    
 s en  2   t    
2
 2

1
3
p CN  vCN  i CN  E EF  I EF  cos     E EF  I EF   cos  2   t     E EF  I EF 
 s en  2   t   
2
2
cos  a  b   cos  a   cos  b   s en  a   s en  b 
cos  2   t     cos  2   t   cos     s en  2   t   s en   
1
1
E EF  I EF   cos  2   t     E EF  I EF   cos  2   t   cos     s en  2   t   s en    
2
2
sen  a  b   sen  a   cos  b   sen  b   cos  a 
s en  2   t     sen  2   t   cos     sen     cos  2   t 
E EF  I EF 
3
3
3
 s en  2   t     E EF  I EF 
 sen  2   t   cos     E EF  I EF 
 sen     cos  2   t 
2
2
2
1
pCN  vCN  i CN  E EF  I EF  cos     E EF  IEF   cos  2   t   cos     s en  2   t   s en      ...
2
3
3
 E EF  I EF 
 sen  2   t   cos     E EF  I EF 
 sen     cos  2   t 
2
2
1
1
pCN  vCN  i CN  E EF  I EF  cos     E EF  I EF   cos     cos  2   t   E EF  I EF   s en     s en  2   t   ...
2
2
3
3
 E EF  I EF 
 cos     sen  2   t   E EF  I EF 
 sen     cos  2   t 
2
2
1
1
p CN  v CN  i CN  E EF  I EF  cos     E EF  IEF  cos      cos  2   t   E EF  I EF  s en      s en  2   t   ...
2
2
3
3
 E EF  I EF  cos    
 sen  2   t   E EF  I EF  sen    
 cos  2   t 
2
2
1
1


p CN  v CN  i CN  E EF  I EF  cos     1   cos  2   t    E EF  I EF  s en      s en  2   t   ...
2
2


 E EF  I EF  cos    
3
3
 sen  2   t   E EF  I EF  sen    
 cos  2   t 
2
2
1
1
3
3


p CN  v BN  i BN  P  1   cos  2   t    Q   s en  2   t   P 
 sen  2   t   Q 
 cos  2   t 
2
2
2
2


Q
1
3
3


p CN  v BN  i BN  P  1   cos  2   t      P 
 cos  2   t 
  sen  2   t   Q 
2
2 
2


2
Potência Instantânea Total
p T  p AN  p BN  p CN
pT  P  1  cos  2   t    Q  s en  2   t   ...
Q
1
3
3


 cos  2   t   ...
P  1   cos  2   t      P 
  sen  2   t   Q 
2
2 
2


2
Q
1
3
3


 cos  2   t 
P  1   cos  2   t      P 
  sen  2   t   Q 
2
2 
2


2
p T  P  1  cos  2   t    Q  s en  2   t   ...
1
Q


 sen  2   t   ...
P  1   cos  2   t   
2
2


1
Q


 sen  2   t 
P  1   cos  2   t   
2
2


p T  P  1  cos  2   t    Q  s en  2   t   ...
P   2  cos  2   t    Q  sen  2   t 
pT  3  P
A potência instantânea total, fornecida pelo circuito trifásico equilibrado, p T  3  E EF  I EF  cos     3  P é
igual à potência ativa ou real, em Watts, sendo sempre positiva ou nula, caso o fator de potência, cos    ,
seja zero (cargas puramente reativas, indutivas ou capacitivas). Esta potência instantânea é igual à potência
média, sendo por isso, invariante no tempo.
Bibliografia
[1] – Lab II: Lecture on Three-Phase Power Systems
D. Niebur , disponível em:
http://power.ece.drexel.edu/WebCourses/ECEL-302/LABII_Lecture_ThreePhaseComplexPowerDN.pdf
[2] – Introduction to Power Systems, Class Notes Chapter 3, Polyphase Networks
Massachusetts Institute of Technology, Department of Electrical Engineering and Computer Science
J.L. Kirtley Jr., disponível em
http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-061-introduction-to-electricpower-systems-spring-2011/readings/MIT6_061S11_ch3.pdf
[3] – Advanteges of the Instantaneous Reactive Power Definitions in Three Phase System Measurements
José manuel Aller et alii.
IEEE Power Engineering Review, Junho de 1999, disponível em:
http://prof.usb.ve/jaller/PPI_papers/paper_08_99.pdf