Plano Colégio Dona Isabel - atividade 8 - IFRS

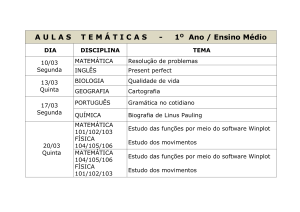
COLÉGIO ESTADUAL DONA ISABEL - PIBID
Bolsistas: Darlã Nogara Oliveira, Leidi Simonin, Maiara Ghiggi e Pitias
Beckestein Paz
Supervisora: Daiane Passari
Disciplina: Matemática
Série: 1º Ensino Médio
Turmas: MA1, MA2, MA3 e MA4
Carga horária: 10 períodos (8h)
Conteúdo: Funções de 1º e 2º graus
Objetivo aula 1: Ao final da primeira aula o aluno deverá ser capaz de
construir gráficos de funções de primeiro grau no winplot, visualizando no
gráfico da função informações como: deslocamento da função, raízes,
crescimento e decrescimento. Conseguindo usá-lo como ferramenta para
construção do conhecimento.
Objetivo aula 2: Ao final da segunda aula o aluno deverá ser capaz de
construir gráficos de funções de segundo grau, no software winplot,
visualizando: a concavidade da parábola, os vértices, as raízes, o domínio, a
imagem, desenvolvendo noções de função quadrática. Utilizar o aplicativo para
esboço de gráfico das funções estudadas.
Recursos: Software Winplot.
Metodologia: O professor deverá iniciar a aula apresentando o software para a
turma, explicando alguns comandos básicos, deixando um tempo para que eles
explorem o programa, tentando relacioná-lo com o conteúdo de funções.
O Software
1 - Abrindo o Winplot
. (trazido e apresentado
Para abrir o Winplot, clique duas vezes no ícone
pelas bolsistas e instalado pelos alunos). Abrirá a caixa:
Clique (uma vez) no botão
Clique no botão
Clique no botão
coluna abaixo do botão:
. Surgirá uma coluna:
. Abrirá a janela semnome1 :
para introduzir uma equação nova e surgirá uma
As equações podem ser inseridas na formas da figura acima (opções de 1 a 4).
Para trabalharmos funções de primeiro e segundo graus utilizaremos a opção
1, equação explícita.
2 - Criando gráficos de funções do 1º grau
Na janela y=f(x), digite no espaço
, a função f(x)
= (1/2)x – 1.
Clique no botão
.
Na janela de gráfico (semnome1.wp2) aparecerá o gráfico da função digitada.
3 - Criando novos gráficos de funções na mesma janela senome1.wp2
Para introduzir novos gráficos, use a janela.
EXERCÍCIOS FUNÇÕES de 1º GRAU - f(x) = ax + b
1) Visualize as funções abaixo, todas em um mesmo gráfico, no Winplot e anote suas
conclusões em relação ao deslocamento no eixo das ordenadas:
f(x) = x
f(x) = x + 1
f(x) = x + 2
f(x) = x + 3
2) Faça o mesmo agora com as funções abaixo:
y = 2x
y = 2x - 2
y = 2x - 4
y = 2x - 6
3) Atribua valores para o x e encontre y nas funções abaixo. Verifique, através do
Winplot, se você achou os valores corretos:
f(x) = 2x + 3
f(x) = - 3x – 2
x
y
x
y
x
y
f(x) = - 2x + 1
4) Das funções abaixo, quais são crescente e quais são decrescente, e diga em que
ponto cada reta intercepta o eixo das ordenas. (Teste o gráfico dessas funções no
Winplot)
a) f(x)= 2x – 4 _______ Ponto: (___,____)
b) f(x)= 3x + 1 _______ Ponto: (___,____)
c) f(x)= - 2x – 3 ______ Ponto: (___,____)
d) f(x)= 4x – 2 _______ Ponto: (___,____)
e) f(x)= - 3x -2 _______ Ponto: (___,____)
f) f(x)= 2x + 3 _______ Ponto: (___,____)
5) Teste as funções abaixo, primeiro as da coluna A e depois as funções da Coluna B,
no Winplot e escreva suas conclusões com relação a declividade da reta, analisando o
coeficiente angular:
Coluna
A
f (x)= 4x
f(x)= 3x
Coluna B
f (x)= - 5x
f(x)= - 3x
f(x)= x
f(x)=0,8x
f(x)= 0,5
x
f(x)= - x
f(x)= - 0,8x
f(x) = 0,3x
4 - Criando gráficos de funções do 2º grau
Para obtermos xn devemos digitar na coluna da janela y = f(x), x^n. Na janela
y=f(x), digite no espaço
, a função f(x) = x^2 – 2x
–2
Na janela de gráfico (semnome2.wp2) aparecerá o gráfico da função digitada.
Para obtermos xn devemos digitar na coluna
da janela y = f(x), x^n.
EXERCÍCIOS FUNÇÕES de 2º GRAU - f(x) = ax2 + bx + c
Visualize as funções abaixo, uma de cada vez, no Winplot e marque a resposta
correta:
1) f(x) = x2 – 3x – 4
Quais são as raízes da
função:______________________________________________
A parábola está voltada para: ( ) cima, ( ) baixo. Por quê?
______________________
A função toca o eixo dos x?___________
Em quantos pontos:___________ . Quais são
eles:_______________________________
Então o ∆ é: ( ) ∆ > 0 , ( ) ∆ = 0, ( ) ∆ < 0.
Em que ponto a parábola corta o eixo das
ordenadas?__________________________
A função tem ponto de: ( ) máximo ou ( ) mínimo.
A coordenada do vértice é: _________________
2) f(x) = - x2 + 3x
Quais são as raízes da
função:______________________________________________
A parábola está voltada para: ( ) cima, ( ) baixo. Por quê?
______________________
A função toca o eixo dos x?___________
Em quantos pontos:___________ . Quais são
eles:_______________________________
Então o ∆ é: ( ) ∆ > 0 , ( ) ∆ = 0, ( ) ∆ < 0.
Em que ponto a parábola corta o eixo das
ordenadas?__________________________
A função tem ponto de: ( ) máximo ou ( ) mínimo.
A coordenada do vértice é: _________________
3) y = 2x2 + 8x
Quais são as raízes da
função:_____________________________________________
A parábola está voltada para: ( ) cima, ( ) baixo. Por quê?
______________________
A função toca o eixo dos x?___________.
Em quantos pontos:___________ . Quais são
eles:_____________________________ __
Então o ∆ é: ( ) ∆ > 0 , ( ) ∆ = 0, ( ) ∆ < 0.
Em que ponto a parábola corta o eixo das
ordenadas?__________________________
A função tem ponto de: ( ) máximo ou ( ) mínimo.
A coordenada do vértice é: __________________
4) f(x) = x2 – 4
Quais são as raízes da
função:______________________________________________
A parábola está voltada para: ( ) cima, ( ) baixo. Por quê?
______________________
A função toca o eixo dos x?___________
Em quantos pontos:___________ . Quais são
eles:_______________________________
Então o ∆ é: ( ) ∆ > 0 , ( ) ∆ = 0, ( ) ∆ < 0.
Em que ponto a parábola corta o eixo das
ordenadas?__________________________
A função tem ponto de: ( ) máximo ou ( ) mínimo.
A coordenada do vértice é: __________________
5) y = - 2x2 + 18
Quais são as raízes da
função:______________________________________________
A parábola está voltada para: ( ) cima, ( ) baixo. Por quê?
______________________
A função toca o eixo dos x?___________
Em quantos pontos:___________ . Quais são
eles:_______________________________
Então o ∆ é: ( ) ∆ > 0 , ( ) ∆ = 0, ( ) ∆ < 0.
Em que ponto a parábola corta o eixo das
ordenadas?__________________________
A função tem ponto de: ( ) máximo ou ( ) mínimo.
A coordenada do vértice é: __________________
Avaliação: Serão avaliados o interesse em conhecer o programa WIMPLOT e
a participação dos alunos durante a aula, na execução do software como
auxilio no desenvolvimento das atividades.
Resultados: Com as atividades desenvolvidas com o auxílio do winplot foi
identificado que os alunos, através da visualização dos gráficos de funções de
primeiro e segundo grau, compreenderam os conceitos de, respectivamente:
deslocamento da função, raízes, crescimento e decrescimento; e concavidade
da parábola, vértices, raízes, domínio e imagem.
Bibliografia:
BARRETO FILHO, Benigno. XAVIER DA SILVA, Claudio. Matemática aula por
aula (coleção matemática aula por aula), 1ª edição, São Paulo: FTD, 2003.
DANTE, Luiz Roberto. Matemática: contexto e aplicações, 3ª edição, 4
volumes, São Paulo: Ática, 2008.
GIOVANNI, José Ruy. BONJORNO, José Roberto. Matemática completa
(coleção matemática completa), 2ª edição renovada, São Paulo: FTD, 2005.
RIBEIRO, Jackson. Matemática: ciência, linguagem e tecnologia, 1: ensino
médio. São Paulo: Scipione, 2010.
PAIVA, Manoel. Matemática:Paiva. 1ª edição, 3 volumes, São Paula:
Modernas, 2009.
SOUZA, Joamir Roberto de. Novo olhar matemático (coleção novo olhar v.1),
1ª
edição,
São
Paulo:
FTD,
2010.
http://math.exeter.edu/rparris/peanut/Explorando%20Winplot%20%20Vol%201.pdf acesso em 06/06/2013