mc38282283053 - o ensino de funções com o auxílio do winplot

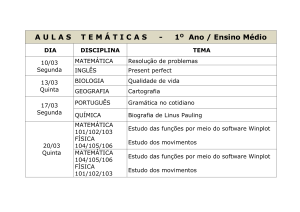
O ENSINO DE FUNÇÕES COM O AUXÍLIO DO WINPLOT
Clarice Favaretto Salvador
Universidade Paulista (UNIP)
[email protected]
A proposta para este mini-curso decorre do resultado de experiências positivas que
tive nestes últimos anos ensinando disciplinas como o Cálculo Diferencial e Integral
com o apoio do software WINPLOT. Ele é um programa livre (portanto acessível a
todos), que gera gráficos em duas ou três dimensões, a partir de funções ou equações, de
modo simples, rápido e direto, tendo excelentes resultados. Além disso, é um programa
pequeno, com menos de 600 Kb (cabendo até num disquete), que pode ser rodado nos
sistemas WINDOWS 95/98/ME/2K/XP, é sempre atualizado e existe sua versão em
português. Fiquei fascinada tanto pelos recursos do WINPLOT, bem como pela reação
de meus alunos perante esta nova forma de ver a matemática. Essa minha impressão
vem reforçar o depoimento do professor da Unicamp, Herbert Bazzani, no projeto
Cálculo com Aplicações [2] : “Coisas que você imaginava antes hoje o computador
faz.(...) Então você consegue imaginar outras coisas, além daquilo que você
imaginava”.
Dessa minha experiência surgiu a proposta deste mini-curso.
Como ponto de partida apresentarei algumas funções básicas do software,
principalmente as necessárias para o estudo dos tópicos propostos.
Na definição das funções lineares f ( x)  ax  b é possível, com o auxílio do Winplot,
ver as variações de seu gráfico em função de mudanças nos valores dos parâmetros a e
b . Fazendo somente a variação de a observam-se as propriedades de crescimento e
decrescimento da função, a interpretação de a como taxa de variação da função, etc.
Com a variação de b , o deslocamento de forma paralela da reta (sem mudanças na
inclinação). É possível também construir uma família de retas com vários valores de
a ou de b e animar utilizando a variação do outro.
Exemplos:
2
y
y
Função f ( x) ax  b
Variação de a 
Função f ( x) ax  b
Variação de b 




x








x
















Analogamente, no estudo das funções quadráticas




f ( x)  ax 2  bx  c pode-se
observar os efeitos das mudanças nos parâmetros a , b e c no gráfico da mesma. Por
exemplo, mudanças na concavidade da parábola, nas intersecções com os eixos
coordenados, vértice da parábola, etc.
Exemplos:
y
y
Função f ( x) ax 2  bx  c
Variação de a 






x



















Função f ( x)  ax 2  bx  c
Variação de b

x


Função f ( x) ax 2  bx  c
Variação de b




3
y




x











2
ax  bx  c
Função f ( x) 
Variação de c

Para funções trigonométricas, especialmente as funções seno e cosseno, utilizarei a
animação para relacionar suas definições através do circulo trigonométrico com os
gráficos de tais funções no plano cartesiano.
f ( x)  a.sen(b.x  c) podem ser observados os
Trabalhando com funções do tipo
efeitos dos parâmetros a , b e c na amplitude da função, no período e no deslocamento
de seu gráfico da direção do eixo das coordenadas.
Exemplos:
y
y




x









x









Função f ( x)  asen (bx  c)
Variação de 
a

Função f ( x)  asen (bx  c)

Variação de b


4
y

x










Função f ( x)  asen (bx  c)
Variação de c

Para todas as funções citadas é possível encontrar, geometricamente e algebricamente,
seus zeros reais e seus pontos de máximo ou de mínimo locais, acompanhados do maior
ou menor valor da função, respectivamente.
Para finalizar serão propostas atividades que deverão ser desenvolvidas pelos
participantes, com o objetivo principal de mostrar quão fácil é a utilização do software
em diversas atividades.
Referências Bibliográficas
[1] BIANCHINI, E. e PACCOLA H. Curso de Matemática, Volume Único. Ed.
Moderna, São Paulo, 1993.
[2] Figueiredo, Vera L.X, Mello Margarida P. & Santos, Sandra A. Cálculo com
Aplicações: Atividades Computacionais e Projetos. Campinas – SP: IMECC, 2005;
[3] IEZZI, G. e MURAKAMI, C. Conjuntos e Funções, Coleção Fundamentos de
Matemática Elementar, vol 1, Ed. Atual, São Paulo, 1985.
[4] Jesus, Adelmo Ribeiro. WINPLOT – Versão em Português, Salvador: Disponível
em http://math.exeter.edu/rparris/
[5] Souza, Sérgio Albuquerque. Usando o WINPLOT, , out. 2004, Disponível em:
<http://www.mat.ufpb.br/~sergio/winplot/winplot.html>