Vunesp 2003 - Conhecimentos específicos

Questão 11
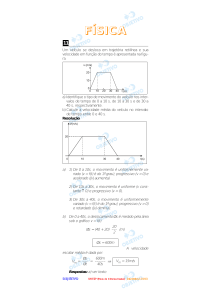
Um veículo se desloca em trajetória retilínea
e sua velocidade em função do tempo é apresentada na figura.
a) Identifique o tipo de movimento do veículo
nos intervalos de tempo de 0 a 10 s, de 10 a
30 s e de 30 a 40 s, respectivamente.
b) Calcule a velocidade média do veículo no
intervalo de tempo entre 0 e 40 s.
Resposta
a) Da análise do gráfico, temos:
• De 0 a 10 s – movimento retilíneo uniformemente acelerado;
• De 10 a 30 s – movimento retilíneo uniforme;
• De 30 a 40 s – movimento retilíneo uniformemente retardado.
b) No gráfico da velocidade versus tempo, a área
sob a curva é numericamente igual ao deslocamento escalar. Assim temos:
N
(40 + 20) ⋅ 20
A = ∆S ⇒ ∆S =
⇒ ∆S = 600 m
2
Da definição de velocidade escalar média, vem:
vm =
∆S
600
=
⇒
∆t
40
v m = 15 m/ s
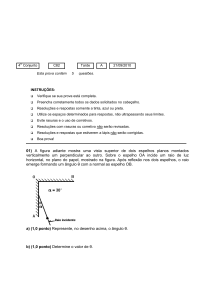
O motociclista salta o vão com certa velocidade u0 e alcança a plataforma inferior, tocando-a com as duas rodas da motocicleta ao
mesmo tempo. Sabendo-se que a distância
entre os eixos das rodas é 1,0 m e admitindo
g = 10 m/s2 , determine:
a) o tempo gasto entre os instantes em que
ele deixa a plataforma superior e atinge a inferior.
b) qual é a menor velocidade com que o motociclista deve deixar a plataforma superior,
para que não caia no fosso.
Resposta
a) Desprezando a resistência do ar, na direção
vertical o motociclista realiza um MUV. Assim, temos:
h =g ⋅
t2
t2
⇒ 1,25 = 10 ⋅
⇒
2
2
t = 0,50 s
b) Desprezando a resistência do ar, na direção horizontal o motociclista realiza um MU.
Considerando que o motociclista deixa a plataforma superior no instante que a roda dianteira
perde contato com esta, a mínima distância horizontal percorrida para não cair no fosso é
∆x = 4,0 + 1,0 = 5,0 m. Assim, temos:
∆x = v ⋅ t ⇒ 5 = v ⋅ 0,5 ⇒
v = 10 m/s (mesma di-
reção e sentido de u 0 )
Questão 12
Um motociclista deseja saltar um fosso de
largura d = 4,0 m, que separa duas plataformas horizontais. As plataformas estão em níveis diferentes, sendo que a primeira encontra-se a uma altura h = 1,25 m acima do nível
da segunda, como mostra a figura.
Observação: se considerarmos que o motociclista
deixa a plataforma quando a roda traseira perde
contato com esta, a distância mínima percorrida
para não cair no fosso é ∆x = 4,0 m. Assim, a me4,0
nor velocidade seria v =
= 8,0 m/s. Na verda0,5
de, o mais correto seria analisar o movimento do
centro de massa do sistema moto-motociclista,
mas a falta de dados não permite.
física 2
Questão 13
Considere dois blocos A e B, com massas mA
e mB respectivamente, em um plano inclinado, como apresentado na figura.
2ª) Se o bloco A desce retardado, analogamente
temos:
g
T − m A g sen 30 o = m A ⋅
4
⇒
g
mB g − T = mB ⋅
4
m
m
1
⇒ mB g − m A g ⋅
= A ⋅g + B ⋅g ⇒
2
4
4
⇒
Desprezando forças de atrito, representando
a aceleração da gravidade por g e utilizando
dados da tabela
θ
30o
o
60
cos θ
sen θ
3 /2
1/2
1/2
3 /2
a) determine a razão mA /mB para que os blocos A e B permaneçam em equilíbrio estático.
b) determine a razão mA /mB para que o bloco A desça o plano com aceleração g/4.
Resposta
As forças sobre os blocos A e B são dadas por:
mA
=1
mB
Questão 14
Duas massas A e B locomovem-se no mesmo
sentido ao longo do eixo x, com velocidades
v A = 2,0 m/s e vB = 6,0 m/s, respectivamente.
Em dado momento, a massa B alcança A, colidindo elasticamente com ela. Imediatamente após a colisão, a massa B fica em repouso e
a massa A é impulsionada com velocidade
u A = 4 ,0 m/s na direção x.
a) Calcule a razão R = E A /EB entre as energias cinéticas das massas A e B antes da colisão.
b) Calcule o valor da força média que agiu sobre a massa A, sabendo-se que seu valor é
mA = 2,0 kg e que as massas estiveram em
contato durante 8,0 × 10 −4 s.
Resposta
a) Quando A e B estão em equilíbrio estático, temos:
T = m A g sen 30 o
1
⇒ mA g ⋅
= mB g ⇒
2
T = mB g
⇒
mA
= 2
mB
b) Quando A desce o plano com aceleração g/4,
temos duas possibilidades:
1ª) Se o bloco A desce acelerado, do Princípio
Fundamental da Dinâmica, vem:
g
m A g sen 30 o − T = m A ⋅
4
⇒
g
T − mB g = mB ⋅
4
m
m
1
⇒ mA g ⋅
− mB g = A ⋅ g + B ⋅ g ⇒
4
2
4
⇒
mA
= 5
mB
a) Sendo o sistema isolado, temos:
Qantes = Qdepois ⇒ m Av A + mBv B = m Au A ⇒
⇒ m A ⋅ 2,0 + mB ⋅ 6,0 = m A ⋅ 4,0 ⇒
⇒ m A = 3 mB
A razão R é dada por:
m A ⋅ v A2
E
3 mB ⋅ 2,0 2
2
R = A =
=
⇒
2
EB
mB ⋅ v B
mB ⋅ 6,0 2
2
⇒
R =
1
3
b) Do Teorema do Impulso, aplicado para a massa A, vem:
IR = ∆Q ⇒ Fm ⋅ ∆t = m A (u A − v A ) ⇒
⇒ Fm ⋅ 8,0 ⋅ 10 −4 = 2,0(4,0 − 2,0) ⇒
⇒
Fm = 5,0 ⋅ 10 3 N
física 3
Questão 15
Questão 16
O volume de líquido deslocado
pela porção submersa de um
bloco que nele está flutuando é
V0 . A seguir, ata-se ao bloco
uma esfera mais densa que o
líquido, por meio de um fio muito fino, como
mostra a figura. Verifica-se que o bloco continua flutuando, mas o volume total de líquido
deslocado passa a ser V0 + 2V .
Sabendo-se que a massa específica do líquido
é ρL , que o volume da esfera é V, e representando a aceleração da gravidade por g, encontre, em função dos dados apresentados,
a) a massa específica ρ da esfera;
b) a tensão T no fio.
A figura representa um espelho plano E e
uma linha CD a sua frente. Há um ponto x A
no eixo x, de onde um dos olhos do observador
vê, por reflexão, a linha em toda a sua extensão e ocupando o espelho todo.
Resposta
a) Da situação inicial (apenas o bloco flutuando) e
do Princípio de Arquimedes, temos que o peso P
do bloco é ρLV0 g .
Na situação final, as forças que atuam nos corpos
são indicadas na figura a seguir:
a) Determine o valor de x A .
b) A seguir, desloca-se o espelho 10 cm para
baixo, paralelamente ao eixo y. Determine as
coordenadas x B e y B do ponto onde deve estar o olho do observador para que ele possa
ver a linha CD ocupando todo o espelho.
Resposta
a) Pela propriedade da simetria, aplicada ao espelho plano, temos a figura a seguir:
Do equilíbrio nos dois corpos, temos:
T =E −P
⇒ E − P = P’ − E’ ⇒
T = P’ − E ’
⇒ ρL (V0 + 2V)g − ρLV0 g = ρVg − ρLVg ⇒
⇒
ρ = 3 ρL
b) Da equação de equilíbrio para o bloco, vem:
T = E − P ⇒ T = ρL (V0 + 2V)g − ρLV0 g ⇒
⇒
T = 2 ρLVg
física 4
Portanto, da figura, um dos olhos do observador
deve ocupar o ponto
x A = 100 cm .
b) Pela propriedade da simetria, aplicada ao espelho plano deslocado 10 cm para baixo, temos a
figura a seguir:
θ
o
sen θ
cos θ
1/2
3 /2
o
2 /2
2 /2
o
3 /2
1/2
30
45
60
a) a velocidade v2 da onda refratada no meio 2.
b) o comprimento de onda λ 2 da onda refratada no meio 2.
Resposta
a) Pela Lei da Refração, temos:
sen i1
v
sen 30 o
340
= 1 ⇒
=
⇒
sen i 2
v2
v2
sen 45 o
1
340
⇒ 2 =
⇒ v 2 = 481 m /s
v2
2
2
b) Como a freqüência não muda na refração, da
equação fundamental da ondulatória, temos:
v 2 = λ 2 ⋅ f ⇒ 481 = λ 2 ⋅ 20 ⇒ λ 2 = 24 m
Portanto, da figura, as coordenadas devem ser
xB = 100 cm
e
y B = −30 cm .
Questão 17
Uma onda plana de freqüência f = 20 Hz,
propagando-se com velocidade v1 = 340 m/s
no meio 1, refrata-se ao incidir na superfície
de separação entre o meio 1 e o meio 2, como
indicado na figura.
Questão 18
Um gás, que se comporta como gás ideal, sofre expansão sem alteração de temperatura,
quando recebe uma quantidade de calor
Q = 6 J.
a) Determine o valor ∆E da variação da energia interna do gás.
b) Determine o valor do trabalho T realizado
pelo gás durante esse processo.
Resposta
a) Sendo a transformação isotérmica, não há variação da energia interna do gás, ou seja,
∆E = 0.
b) Da 1ª Lei da Termodinâmica, temos:
0
Q = T + ∆E ⇒ T = 6 J
Sabendo-se que as frentes de onda plana incidente e refratada formam, com a superfície
de separação, ângulos de 30o e 45o respectivamente, determine, utilizando a tabela seguinte
Questão 19
Uma lâmpada incandescente (de filamento)
apresenta em seu rótulo as seguintes especificações: 60W e 120 V.
física 5
Determine
a) a corrente elétrica I que deverá circular
pela lâmpada, se ela for conectada a uma fonte de 120 V.
b) a resistência elétrica R apresentada pela
lâmpada, supondo que ela esteja funcionando
de acordo com as especificações.
Resposta
a) Na condição nominal de funcionamento, temos:
P = U ⋅ I ⇒ 60 = 120 ⋅ I ⇒
I = 0,50 A
b) Da definição de resistência elétrica, vem:
U
120
R =
=
⇒ R = 240 Ω
I
0,5