Função Exponencial

COLÉGIO PEDRO II – CAMPUS ENGENHO NOVO II
Adição de Arcos, Equações e Funções Trigonométricas – MAT 2
1ª SERIE - EM
DOCENTE: GEISA
Setembro de 2016
Coord. RENATO
TURMA: 110__
NOME:
NÚMERO:
Adição de Arcos, Arcos Duplos, Equações e Funções Trigonométricas
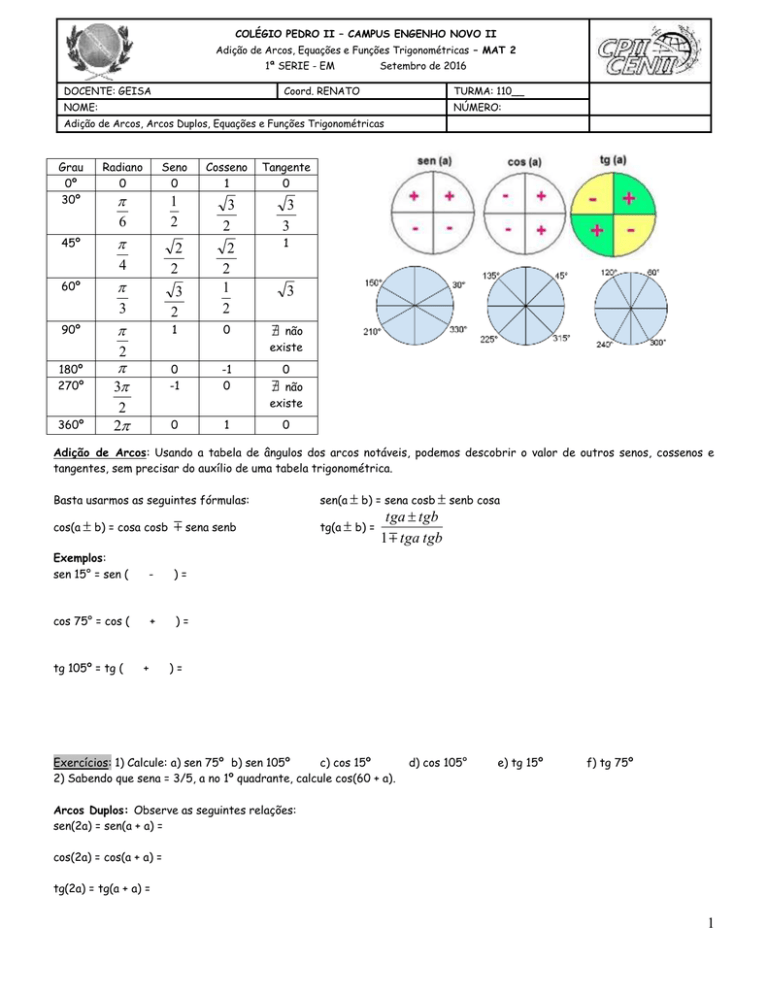
Grau
0º
30º
45º
60º
90º
180º
270º
360º
Radiano
0

6

4

3

2

3
2
2
Seno
0
Cosseno
1
Tangente
0
1
2
3
3
2
2
3
2
3
2
2
2
1
2
1
0
0
-1
-1
0
0
1
1
3

não
existe

0
não
existe
0
Adição de Arcos: Usando a tabela de ângulos dos arcos notáveis, podemos descobrir o valor de outros senos, cossenos e
tangentes, sem precisar do auxílio de uma tabela trigonométrica.
Basta usarmos as seguintes fórmulas:
sen(a  b) = sena cosb  senb cosa
cos(a  b) = cosa cosb
 sena senb
tg(a  b) =
Exemplos:
sen 15° = sen (
-
)=
cos 75° = cos (
+
)=
tg 105º = tg (
+
tga  tgb
1  tga tgb
)=
Exercícios: 1) Calcule: a) sen 75º b) sen 105º
c) cos 15º
2) Sabendo que sena = 3/5, a no 1º quadrante, calcule cos(60 + a).
d) cos 105°
e) tg 15º
f) tg 75º
Arcos Duplos: Observe as seguintes relações:
sen(2a) = sen(a + a) =
cos(2a) = cos(a + a) =
tg(2a) = tg(a + a) =
1
Apostila 3 Trigonometria – MAT 2
1ª SERIE - EM
Setembro de 2016
Adição de Arcos, Arcos Duplos, Equações e Funções Trigonométricas.
Logo, calculando sen 60, pela fórmula acima temos:
Outros exemplos: 1) Sabendo que senx = 3/5, calcule sen 2x sendo x no 2º quadrante.
2) Sabendo que cox x = 1/3, calcule cos 2x
3) Sendo tg x = 5 calcule tg 2x
Exercícios: 1) Sendo sen x = -5/13 e x no 3º quadrante calcule sen(2x) e cos(2x).
2) Dado tgx = 3 calcule tg(2x).
3) Calcule cos150, sen180 e tg210 usando as fórmulas dos arcos duplos.
---------Algumas equações trigonométricas: Já vimos as equações imediatas que justamente possuem este nome por possuírem
resultado imediato apenas consultando a tabela de valores, fazendo a redução ao 1º quadrante (quando necessário) e sabendo
os sinais das relações trigonométricas nos 4 quadrantes. Vejamos outros exemplos de equações não imediatas.
1) 3sen²x - 4senx + 1 = 0
a) sendo x no primeiro quadrante
b) sendo x um ângulo qualquer
2) 4cox²x + 5senx – 5 = 0
a) sendo x no segundo quadrante
b) sendo x um ângulo qualquer
2
Apostila 3 Trigonometria – MAT 2
1ª SERIE - EM
Setembro de 2016
Adição de Arcos, Arcos Duplos, Equações e Funções Trigonométricas.
Exercícios: 1) senx = 3 cos x (x no 3º quadrante)
3) 2sen²x + cosx – 1 = 0
a) x na 1ª volta
4) 2sen² x – sen x – 1 = 0
a) x na 1ª volta
5) cos² x – 4 cosx + 3 = 0
a) x na 1ª volta
6) tg² x – tg x = 0
7)
2) senx – cos² x = 1
b) x um ângulo qualquer
b) x um ângulo qualquer
b) x um ângulo qualquer
3 + 2 tgx
 tgx  0
5
---------Funções Trigonométricas
Seno de um arco
Sinais do seno
Seno dos arcos notáveis
x
sen(x)
1/2
30º =  /6 rad
 /4 rad
60º =  /3 rad
45º =
2 /2
3 /2
Gráfico da função seno
x
sen(x)
0º = 0 rad
0
1

rad
90º =
2
180º =  rad
3
rad
270º =
2
360º = 2 rad
0
-1
0
Outros gráficos da função seno: Exemplo: 1) f(x) = sen(2x)
2x
x
sen(2x)
0
0
1

2

0
3
2
2
-1
0
3
Apostila 3 Trigonometria – MAT 2
1ª SERIE - EM
Setembro de 2016
Adição de Arcos, Arcos Duplos, Equações e Funções Trigonométricas.
2) f(x) = sen(x/3)
x/3
x
sen(x/3)
0
0
1

2

0
3
2
2
-1
0
Exercício: Construa o gráfico da função f(x) = sen(4x) e f(x) = sen(x/2)
Exemplo3: f(x) = 2sen(x)
x
senx
2senx
0
0
1

2

0
3
2
2
-1
0
Exercícios: Construa os gráficos: a) f(x) = 3sen(x)
b) f(x) = 2sen(x) + 1
---------Cosseno de um arco
Sinais do cosseno
Cosseno dos arcos notáveis
x
cos(x)
 /6 rad
45º =  /4 rad
60º =  /3 rad
30º =
3 /2
2 /2
1/2
Gráfico da função cosseno
x
cos(x)
0º = 0 rad
1
0

rad
90º =
180º =
270º =
360º =
2
 rad
3
rad
2
2 rad
-1
0
1
4
Apostila 3 Trigonometria – MAT 2
1ª SERIE - EM
Setembro de 2016
Adição de Arcos, Arcos Duplos, Equações e Funções Trigonométricas.
Outros gráficos da função cosseno: Exemplo1: f(x) = cos(x/2)
x
x
x
cos( )
2
2
0
1
0

2
-1

3
0
2
2
1
Exemplo 2: f(x) = cos(x) - 1
x
cosx
cosx – 1
0

2

3
2
2
Exercícios: Construa o gráfico das funções:
a) f(x) = cos(3x)
b) f(x) = 2cos(x)
d) f(x) = cos(4x)
e) f(x) = cos(x/4)
c) f(x) = 2cos(x) + 2
f) f(x) = 3 cosx + 1
________________________________________________________________________________________
Imagens das funções sen(x) e cos(x)
Analisando os gráficos já estudados percebemos que os gráficos das funções sen(x) e cos(x) estão sempre entre os valores -1
e 1. Portanto para resolver equações do tipo sen(x) = 3k+3 basta resolvermos duas simples inequações:
-1  3k+3  1, ou seja, -1  3k+3 e 3k+3  1
Exercícios: a) cos(x) = 5k - 10
b) sen(x) = 2k - 3
c) sen(x) = -k + 6
d) cos(x) = 4k - 5
---------Tangente de um arco
Sinais da tangente
Tangente dos arcos notáveis
x
tg(x)
 /6 rad
45º =  /4 rad
60º =  /3 rad
30º =
3 /3
1
3
5
Apostila 3 Trigonometria – MAT 2
1ª SERIE - EM
Setembro de 2016
Adição de Arcos, Arcos Duplos, Equações e Funções Trigonométricas.
Gráfico da função tangente
x
tg(x)
0º = 0 rad
0
90º =

rad
2
180º =  rad
3
rad
270º =
2
360º = 2 rad
 (não
existe)
0
 (não
existe)
0
Outros gráficos da função tangente: Exemplo1: f(x) = 2tg(x) + 1
x
tgx
2tgx + 1
0

2

3
2
2
Exercícios: f(x) = tg(2x) e f(x) = tg(x/2)
6