Resolução: Trigonometria no Ciclo

CAPÍTULO
11
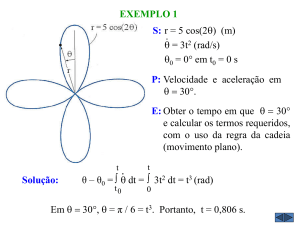
Resolução: Trigonometria
no Ciclo
Resposta da questão 3:
[B]
Medida do arco em rad:
5π
rad.
6
5π
rad = 150°.
6
Resposta da questão 1:
[B]
Resposta da questão 4:
[D]
Cada minuto do relógio corresponde a 6o, portanto,
α = 60° + 6° = 66°.
Partindo da ideia que enquanto o ponteiro dos minutos se
desloca 60min, o ponteiro das horas se desloca 30°, temos:
60min
54min
30°
β
α = 25°25'− 16°40' = 8°45' = 8,75°
360° _______ 40000km
8,75° ______ x
Logo, β = 27°, portanto o arco pedido mede 66° + 27° =
93°.
Resolvendo a proporção, temos: x = 972,2km.
Calculando, em centímetros, o comprimento do arco de 93°,
temos:
Resposta da questão 5:
[A]
93° ⋅ 2π ⋅ 20
= 31 cm (considerando, π = 3)
360°
Lembrando que uma função está bem definida apenas quando
são fornecidos o domínio, o contradomínio e a lei de
associação, vamos supor que o domínio seja o conjunto dos
números reais, e que o contradomínio seja o intervalo [−1, 5].
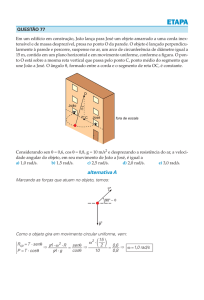
Resposta da questão 2:
[A]
O arco percorrido pelo automóvel corresponde a um ângulo
central cuja medida é
Desse modo, como a imagem da função seno é o intervalo
[−1, 1], deve-se ter
A + B[−1, 1] = [−1, 5] ⇒ [A− B, A + B] = [−1, 5].
21°20 '− 1°20 ' = 20° ⋅
π
rad
180°
Os únicos valores de A e de B que satisfazem a igualdade
são A = 2 e B = 3. Por conseguinte, A ⋅ B = 2 ⋅ 3 = 6.
π
= rad.
9
Portanto, sabendo que o raio da Terra mede 6.730 km, vem
D=
π
⋅ 6730km.
9
Resposta da questão 6:
[B]
Sabendo-se que ângulos suplementares têm cossenos
simétricos, concluímos que:
⎛
⎞
π
2π
f(1) + f(3) + f(5) + f(7) = 4 ⋅ 180 − 54 ⋅ ⎜ cos0 + cos + cos
+ cos π ⎟
3
3
⎝
⎠
= 720.
www.ruilima.com.br | facebook/RuiLima
1
Resposta da questão 7:
[D]
Resposta da questão 10:
[B]
⎛ 3 ⎞ π
⎛ 4 π 3 ⎞
θ ⎜ ⎟ =
⋅ cos ⎜
⋅ ⎟
2
10
⎝ ⎠
⎝ 3 2 ⎠
⎛ 3 ⎞ π
θ ⎜ ⎟ =
⋅ cos ( 2π )
⎝ 2 ⎠ 10
⎛ 3 ⎞ π
θ ⎜ ⎟ =
⋅1
⎝ 2 ⎠ 10
⎛ 3 ⎞ π
θ ⎜ ⎟ =
⎝ 2 ⎠ 10
1° ______111,32km
360° ____ x
x ≅ 40076km2
Resposta da questão 8:
[A]
Mês de Março:
⎛ 2π ⎞
P ( 2 ) = 6000 + 50 ⋅ 2 + 2000 ⋅ cos ⎜
⎟ = 7100
⎝ 6 ⎠
Mês de Julho:
⎛ 6π ⎞
P ( 6 ) = 6000 + 50 ⋅ 6 + 2000 ⋅ cos ⎜
⎟ = 4300
⎝ 6 ⎠
Queda da quantia vendida em porcentagem:
4300 − 7100
; −39,5%
7100
Resposta da questão 9:
[A]
O afastamento vertical da partícula, em relação à posição
inicial, após meio segundo, é
1
1 ⎞ ⎡
1
⎛ 1 ⎞
⎛
⎤
s ⎜ ⎟ − s(0) = 10 + sen ⎜ 10 π ⋅ ⎟ − ⎢10 + sen(10 π ⋅ 0)⎥
4
2 ⎠ ⎣
4
⎝ 2 ⎠
⎝
⎦
1
1
= 10 + sen(5 π) − 10 − sen0
4
4
= 0.
www.ruilima.com.br | facebook/RuiLima
2