Aula 06 – Coordenadas e Trigonometria

Aula 06 – Coordenadas e Trigonometria
Os Sistemas de coordenadas mais utilizados pela física ou pela matemática
são:
• Cartesiano (x,y,z);
• Cilíndrico (ρ,ϕ,z);
• Esférico (r,θ,φ).
O mais apropriado para a maior parte da Astronomia é o sistema esférico,
porém com a simplificação de se ter o raio r constante (apenas os ângulos são
importantes!).
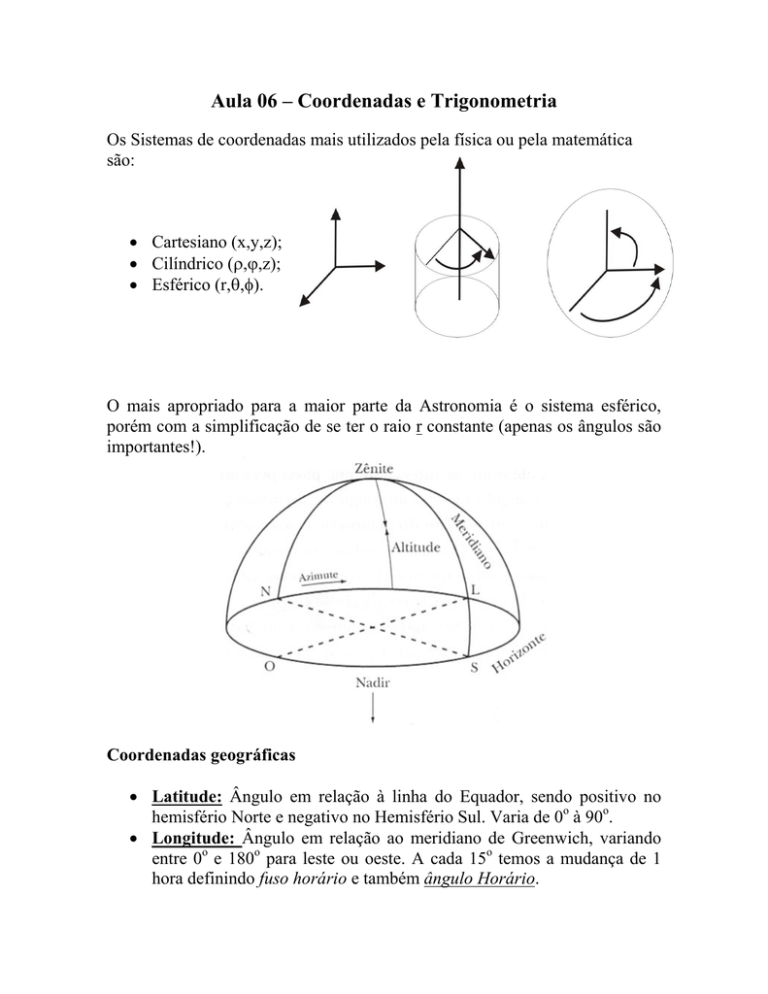
Coordenadas geográficas
• Latitude: Ângulo em relação à linha do Equador, sendo positivo no
hemisfério Norte e negativo no Hemisfério Sul. Varia de 0o à 90o.
• Longitude: Ângulo em relação ao meridiano de Greenwich, variando
entre 0o e 180o para leste ou oeste. A cada 15o temos a mudança de 1
hora definindo fuso horário e também ângulo Horário.
Coordenadas na Esfera Celeste:
São análogas as coordenas geográficas, da seguinte forma:
• Declinação: análoga da latitude, tendo como referência o equador
celeste.
• Ascensão reta: análoga da longitude, porém tendo apenas uma direção
(oeste) e tendo como referência o ponto vernal.
O ponto vernal corresponde ao ponto de encontro entre
o plano da eclíptica e o equador celeste, o qual ocorre no
equinócio da primavera. (assim o equinócio de outono
ocorre com ascensão reta de 180o).
Outros sistemas de coordenadas utilizados são o sistema elíptico, próprio para
se calcula a posição do objeto em sua órbita e o sistema galáctico, que dá a
posição dos objetos distribuídos pela galáxia.
TRIGONOMETRIA ESFÉRICA:
As medidas de distância sobre a superfície não são dadas apenas pela
diferença de coordenadas (latitude, longitude), mas sim pela multiplicação da
diferença pela métrica, que neste caso é o raio. Isto é: d=rθ
Igualmente, a trigonometria sofre algumas modificações, quando passamos do
espaço plano usual para uma superfície esférica.
Triângulo Esférico:
• Soma dos ângulos de um triângulo
esférico não é constante, variando, para
cada triângulo, entre 180o e 270o. De
fato, o excesso a 180o é diretamente
proporcional à área do triângulo.
• A soma dos lados de um triângulo
esférico é maior do que 0o e menor que
180o.
• Os lados maiores estão opostos aos
ângulos maiores.
• A soma de dois lados do triângulo é sempre maior do que o terceiro
lado, e a diferença é sempre menor.
• Cada um dos lados do triângulo é menor que 180o, e isto também se
aplica aos ângulos.
• Para especificar um triângulo esférico é sempre necessário um conjunto
de três elementos, dentre ângulos e lados: (A,A,A); (L,L,L); (A,L,L)...
(para o triângulo convencional, precisamos de apenas dois).
Reescrevendo a lei dos cossenos e a lei dos senos para estes triângulos,
teremos respectivamente (vide figura):
cos a = cos b cos c + sen b sen c cos A
sen a sen b sen c
=
=
sen A sen B sen C
Triângulo de posição
É utilizado para se derivar as coordenadas do
local de observação, sabendo-se a dos astros.
Ou, por outro lado, obter as coordenadas dos
astros, sabendo-se a do local.
Na figura: Pn – Pólo Norte; z= ângulo entre o
Zênite e o astro observado; Z = zênite. A =
ângulo com vértice no Zênite; H= ângulo com
vértice no Pólo Norte.
Substituindo os elementos do triângulo de posição (vide figura) nas leis do
cosseno e do seno, obtemos as relações:
cos z = sen φ sen δ + cos φ cos δ cos H
⇒ cos H = cos z sec φ sec δ − tan φ tan δ
sen δ = sen φ cos z + cos φ sen z cos A
e
⇒ cos A = sen δ csc z sec φ − tan φ cot z
Exemplo:
Para o Sol, temos z=90o. Estando Porto Alegre em φ=-30o, podemos calcular a
duração do dia usando a relação (onde δ é dado pela data, sendo δ=-23o no
solstício de verão):
cos H = − tan φ tan δ
O que dá 14 horas e 10 minutos no dia 21 de Dezembro (lembrando que 150
equivale a 1 hora).