1. (PUC - RJ 2013) Se tgθ 1 e θ pertence ao primeiro quadrante, então cosθ é
igual a:
a) 0
b)
1
2
2
2
3
d)
2
c)
e) 1
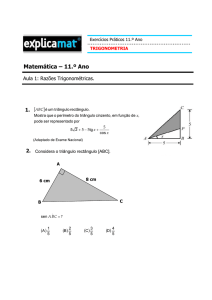
2. (Uepb 2012) Os lados iguais de um triângulo isósceles têm comprimento
3 cm e
os ângulos congruentes medem 30. O perímetro deste triângulo em cm é
a) 2 3 3
b) 2 3 2
c) 8 3
d) 3 3
e) 3 3
3. (PUC - RS 2012) Em uma aula prática de Topografia, os alunos aprendiam a
trabalhar com o teodolito, instrumento usado para medir ângulos. Com o auxílio desse
instrumento, é possível medir a largura y de um rio. De um ponto A, o observador
desloca-se 100 metros na direção do percurso do rio, e então visualiza uma árvore no
ponto C, localizada na margem oposta sob um ângulo de 60°, conforme a figura
abaixo.
Nessas condições, conclui-se que a largura do rio, em
metros, é
a)
100 3
3
100 3
2
c) 100 3
b)
d)
50 3
3
e) 200
ˆ
4. (UFJF 2011) Considere um triângulo ABC retângulo em C e o ângulo BAC.
1
Sendo AC 1 e sen( ) , quanto vale a medida da hipotenusa desse triângulo?
3
a) 3
b)
2 2
3
c) 10
3 2
4
3
e)
2
d)
5. (PUC RJ 2010) O valor de
a)
2 1
b) 2
cos 45 sen30
é:
cos60
c)
2
4
d)
2 1
2
e) 0
Gabarito:
Resposta da questão 1:
[C]
Se θ é um arco do primeiro quadrante e tg θ 1, temos que θ 45.
Portanto,
cos θ cos 45
2
.
2
Resposta da questão 2:
[A]
Considere o triângulo isósceles ABC de base BC. Assim, AB AC 3 cm e
ABC ACB 30. Sendo M o ponto médio de BC, do triângulo AMC, vem
BC
cos ACB
cos30 2
3
AC
MC
BC 3cm.
Portanto, o resultado é
AB AC BC 3 3 3
(2 3 3)cm.
Resposta da questão 3:
[C]
O resultado pedido é dado por tg60
y
y 100 3 m.
100
Resposta da questão 4:
[D]
1
3
Sabendo que AC 1 e sen , vem
sen
BC
1 BC
AB
BC
.
3 AB
3
AB
Aplicando o Teorema de Pitágoras, obtemos:
2
AB
2
AB AC BC AB
1
3
2
2
2
2
2
8 AB
1
9
AB
3
2 2
3 2
.
4
Resposta da questão 5:
[A]
2 1 1
( 2 1)
2
2 2
2 1
1
1
2
2