Farmacodinâmica - Anestesiologia UFSC

2
Farmacodinâmica
Harris S. Rose e David E. Golan
Introdução
Caso
Ligação Fármaco–Receptor
Relações de Dose–Resposta
Relações de Dose–Resposta Graduadas
Relações de Dose–Resposta Quantais
Interações Fármaco–Receptor
Agonistas
Antagonistas
Antagonistas Competitivos dos Receptores
INTRODUÇÃO
Utiliza-se o termo farmacodinâmica para descrever os efeitos de um fármaco no corpo. Tipicamente, esses efeitos são
descritos em termos quantitativos. No capítulo anterior, foram
consideradas as interações moleculares pelas quais os agentes
farmacológicos exercem seus efeitos. Este capítulo trata da integração dessas ações moleculares em um efeito exercido sobre
o organismo como um todo. É importante descrever os efeitos
de um fármaco em termos quantitativos para estabelecer as
faixas de doses apropriadas para os pacientes, bem como para
comparar a potência, a eficácia e a segurança de um fármaco
com outro.
�
Caso
O Almirante X, de 66 anos de idade, é um comandante de submarino aposentado, com história de tabagismo de 70 maços de
cigarros por ano (dois maços por dia durante 35 anos) e história
familiar de coronariopatia. Embora normalmente ignore os conselhos
de seus médicos, toma pravastatina prescrita para reduzir o nível de
colesterol, bem como aspirina para diminuir o risco de oclusão da
artéria coronária.
Um dia, enquanto estava trabalhando em sua carpintaria, o Almirante X começa a sentir um aperto no tórax. A sensação torna-se
rapidamente dolorosa, e a dor começa a irradiar-se pelo braço
esquerdo. Liga para o Serviço de Emergência, e uma ambulância
o transporta até o pronto-socorro mais próximo. Uma vez concluída
a avaliação, constata-se que o Almirante X está tendo um infarto
do miocárdio anterior. Como o hospital não dispõe de laboratório
para cateterismo cardíaco, e como o Almirante X não tem nenhuma contra-indicação específica para a terapia trombolítica (como
Antagonistas Não-Competitivos dos Receptores
Antagonistas Sem Receptores
Agonistas Parciais
Agonistas Inversos
Receptores de Reserva
Conceitos em Terapia
Índice Terapêutico e Janela Terapêutica
Conclusão e Perspectivas Futuras
Leituras Sugeridas
hipertensão não-controlada, história de acidente vascular cerebral
ou cirurgia recente), o médico inicia a terapia com o ativador do
plasminogênio de tipo tecidual (tPA), um agente trombolítico, e
com heparina, um anticoagulante. A administração de uma dose
inadequada desses dois fármacos pode ter conseqüências terríveis
(hemorragia e morte), em virtude de seus baixos índices terapêuticos; por esse motivo, o Almirante X é rigorosamente monitorado, e
o efeito farmacológico da heparina é determinado periodicamente
através do tempo de tromboplastina parcial (TTP). Os sintomas
do Almirante X diminuem nas próximas horas, embora permaneça
no hospital para monitorização. Recebe alta depois de 4 dias, e os
medicamentos prescritos incluem pravastatina, aspirina, atenolol,
lisinopril e clopidogrel para prevenção secundária de infarto do
miocárdio.
QUESTÕES
� 1. Como a interação molecular de um fármaco com o seu
receptor determina a sua potência e eficácia?
� 2. Quais as propriedades de certos fármacos, como a aspirina,
que permitem a sua administração sem monitoração dos
níveis plasmáticos do fármaco, enquanto outros fármacos,
como a heparina, exigem esse tipo de controle?
� 3. Por que o fato de um fármaco ter baixo índice terapêutico
significa que o médico deve ter maior cuidado na sua administração?
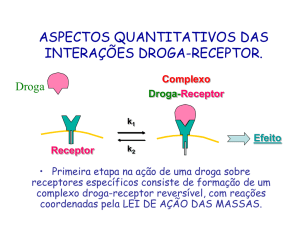
LIGAÇÃO FÁRMACO–RECEPTOR
O estudo da farmacodinâmica baseia-se no conceito da ligação
fármaco–receptor. Quando um fármaco ou um ligante endógeno
(por exemplo, um hormônio ou um neurotransmissor) liga-se
Farmacodinâmica
a seu receptor, pode ocorrer uma resposta como conseqüência dessa interação de ligação. Quando já existir um número
suficiente de receptores ligados (ou “ocupados”) sobre uma
célula ou no seu interior, o efeito cumulativo dessa “ocupação”
dos receptores pode tornar-se aparente nessa célula. Em algum
momento, todos os receptores podem estar ocupados, e pode-se
observar então uma resposta máxima (uma exceção é representada pelos receptores de reserva; ver adiante). Quando a resposta
é desencadeada em muitas células, o efeito pode ser observado
em nível do órgão ou até mesmo no paciente. Entretanto, todo
esse processo começa com a ligação do fármaco ou do ligante
a um receptor (para o propósito dessa discussão, os termos
“fármaco” e “ligante” serão utilizados como sinônimos neste
capítulo). Por conseguinte, seria útil dispor de um modelo que
pudesse descrever de modo acurado a ligação de um fármaco a
um receptor para prever o efeito do fármaco nos níveis molecular, celular, tecidual (órgão) e do organismo como um todo
(paciente). Essa sessão descreve este modelo.
Consideremos o caso mais simples, em que o receptor
encontra-se livre (desocupado) ou reversivelmente ligado a um
fármaco (ocupado). Podemos descrever este caso da seguinte
maneira:
[ LR]
[ LR]
[ Ro ]
=
=
[ Ro ] [ L]
, reorganizada para
[ L ] + Kd
[ L]
[ L]
Observe que o lado direito dessa equação [LR]/[Ro] representa
a fração de todos os receptores disponíveis que estão ligados
ao ligante.
A Fig. 2.1 mostra duas representações gráficas da Equação 2.4 para a ligação de dois fármacos hipotéticos ao mesmo
receptor. Esses gráficos são conhecidos como curvas de ligação fármaco–receptor. A Fig. 2.1A mostra um gráfico linear,
enquanto a Fig. 2.1B mostra o mesmo gráfico em uma escala
A Linear
1,0
Fármaco A
Equação 2.1
Fármaco B
onde L é o ligante (fármaco), R é o receptor livre, e LR, o
complexo fármaco ligado–receptor. Em equilíbrio, a fração de
receptores em cada um desses estados depende da constante
de dissociação, Kd, onde Kd = klivre/kligado. Kd é uma propriedade
intrínseca de qualquer par fármaco–receptor. Apesar de a K d
variar com a temperatura, a temperatura do corpo humano
é relativamente constante, e, portanto, pode-se estabelecer
que a Kd é uma constante para cada combinação de fármaco–receptor.
De acordo com a lei de ação da massa, a relação entre
receptor livre e receptor ligado pode ser descrita da seguinte
maneira:
[ LR]
Equação 2.4
+ Kd
livre
[ L ][ R]
19
Resolvendo [R] e fazendo as devidas substituições na Equação
2.2 a partir da Equação 2.3, obtemos:
k ligado
L + R→
LR
←
k
Kd =
|
, reorganizada para [ LR ] =
[ L ][ R]
Kd
KdA KdB
[L]
B Semilogarítmico
1,0
Fármaco A
Fármaco B
[ L ][ R]
[LR]
0,5
[R0]
0
KdA KdB
[L]
Fig. 2.1 Curvas de ligação ligante–receptor. A. Gráfico linear de ligação
fármaco–receptor para dois fármacos com valores distintos de Kd . B. Gráfico
semilogarítmico da mesma ligação fármaco–receptor. A Kd é a constante de
dissociação em equilíbrio para determinada interação fármaco–receptor — um
valor mais baixo de Kd indica uma interação fármaco–receptor mais firme (de
maior afinidade). Em virtude dessa relação, o Fármaco A, que apresenta uma
Kd mais baixa, irá se ligar a uma maior proporção de receptores totais do
que o Fármaco B em qualquer concentração de fármaco. Observe que a Kd
corresponde à concentração do ligante [L] em que 50% dos receptores estão
ligados (ocupados) pelo ligante. [L] é a concentração de ligante (fármaco) livre
(não-ligado), [LR] é a concentração de complexos ligante–receptor, e Ro é a
concentração total de receptores ocupados e desocupados. Por conseguinte,
[LR]
[Ro ]
Kd
[ L] 
= [ R]  1 +

Kd 
0
Equação 2.2
onde [L] é a concentração de ligante livre, [R] é a concentração de receptor livre, e [LR], a concentração de complexo
ligante–receptor. Como Kd é uma constante, é possível deduzir
algumas propriedades importantes relativas à interação fármaco–receptor a partir dessa equação. Em primeiro lugar, à
medida que aumenta a concentração de ligante, a concentração
de receptores ligados também aumenta. Em segundo lugar, e de
uma forma não tão evidente, à medida que a concentração de
receptores livres aumenta (como pode ocorrer, por exemplo, em
caso de doença ou com exposição repetida a determinado fármaco), a concentração de receptores ligados também aumenta.
Por conseguinte, pode ocorrer um aumento no efeito de um
fármaco em conseqüência de um aumento na concentração do
ligante ou do receptor.
Entretanto, a discussão que se segue ao longo deste capítulo
irá assumir que a concentração do total de receptores é uma
constante, de modo que [LR] + [R] = [Ro]. Isso permite ordenar
a Equação 2.2 da seguinte maneira:
[ Ro ] = [ R] + [ LR] = [ R] +
[LR]
0,5
[R0]
Equação 2.3
é a ocupação fracionária de receptores, ou a fração de receptores totais
ocupados (ligados) pelo ligante.
20
|
Capítulo Dois
semilogarítmica. Como as respostas aos fármacos ocorrem ao
longo de uma ampla faixa de doses (concentrações), o gráfico
semilog é freqüentemente utilizado para apresentar dados de
ligação fármaco–receptor. As duas interações fármaco–receptor
caracterizam-se por diferentes valores de Kd; neste caso, KdA
< KdB.
Na Fig. 2.1, podemos observar que a ligação fármaco–receptor máxima ocorre quando [LR] é igual a [Ro], ou [LR]/[Ro] = 1.
Constatamos também que, de acordo com a Equação 2.4, quando [L] = Kd , então [LR]/[Ro] = Kd/2Kd = 1/2. Por conseguinte,
a Kd pode ser definida como a concentração de ligante em que
50% dos receptores disponíveis estão ocupados.
A Linear
1,0
Fármaco A
Fármaco B
E
0,5
Emáx
0
EC50(A) EC50(B)
RELAÇÕES DE DOSE–RESPOSTA
[L]
B Semilogarítmico
A farmacodinâmica de um fármaco pode ser quantificada pela
relação entre a dose (concentração) do fármaco e a resposta
do organismo (do paciente) a este fármaco. Intuitivamente, o
esperado é que a relação de dose–resposta esteja estreitamente
relacionada com a relação de ligação fármaco–receptor, e verificamos que isso realmente ocorre para muitas combinações
de fármaco–receptor. Por conseguinte, nesse estágio de nossa
discussão, convém partir do princípio de que a resposta a um
fármaco é proporcional à concentração de receptores que estão
ligados (ocupados) pelo fármaco. Essa pressuposição pode ser
quantificada através da seguinte relação:
[ DR]
[ D]
resposta
=
=
[
]
resposta máx.
D
R
+ Kd
[ o]
Equação 2.5
onde [D] é a concentração do fármaco livre, [DR] a concentração do complexo fármaco–receptor, [Ro] a concentração total
de receptores e Kd a constante de dissociação de equilíbrio para
a interação fármaco–receptor. (Observe que o lado direito da
Equação 2.5 equivale à Equação 2.4, sendo o [L] substituído
pelo [D].) A generalização dessa pressuposição é examinada
adiante.
Existem dois tipos principais de relações dose–resposta
— graduada e quantal. A diferença entre os dois métodos é
que as relações de dose–resposta graduadas descrevem o efeito
de várias doses de um fármaco sobre o indivíduo, enquanto
as relações quantais mostram o efeito de várias doses de um
fármaco sobre uma população de indivíduos.
RELAÇÕES DE DOSE–RESPOSTA GRADUADAS
A Fig. 2.2 mostra curvas graduadas de dose–resposta para dois
fármacos hipotéticos que produzem a mesma resposta biológica. As curvas são apresentadas em escalas linear e semilog.
As curvas assemelham-se, quanto à sua forma, àquelas da Fig.
2.1, em concordância com a pressuposição de que a resposta é
proporcional à ocupação dos receptores.
Dois parâmetros importantes — potência e eficácia — podem
ser deduzidos a partir da curva de dose–resposta graduada. A
potência (EC50) de um fármaco refere-se à concentração em
que o fármaco produz 50% de sua resposta máxima. A eficácia
(Emáx.) refere-se à resposta máxima produzida pelo fármaco.
De acordo com a pressuposição anterior, a eficácia pode ser
considerada como o estado em que a sinalização mediada pelo
receptor torna-se máxima, de modo que qualquer quantidade
adicional do fármaco não irá produzir nenhuma resposta adicional. Esse estado é habitualmente alcançado quando todos
1,0
Fármaco A
Fármaco B
E
0,5
Emáx
0
EC50(A) EC50(B)
[L]
Fig. 2.2 Curvas de dose–resposta graduadas. As curvas de dose–resposta
graduadas demonstram o efeito de um fármaco como função de sua
concentração. A. Gráfico linear de curvas de dose–resposta graduadas para dois
fármacos. B. Gráfico semilogarítmico das mesmas curvas de dose–resposta.
Observe a estreita semelhança com a Fig. 2.1: a fração de receptores ocupados
[LR]/[Ro] foi substituída pelo efeito fracionário E/Emáx., onde E é uma resposta
quantificável a determinado fármaco (por exemplo, elevação da pressão arterial).
EC50 é a potência do fármaco ou a concentração em que o fármaco produz
50% de seu efeito máximo. Nesta figura, o Fármaco A é mais potente do que
o Fármaco B, visto que produz metade do efeito máximo numa concentração
mais baixa do que o Fármaco B. Os Fármacos A e B exibem a mesma eficácia
(resposta máxima ao fármaco). Observe que a potência e a eficácia não estão
intrinsecamente relacionadas — um fármaco pode ser extremamente potente,
porém pode ter pouca eficácia, e vice-versa. [L] é a concentração do fármaco,
E é o efeito, Emáx. é a sua eficácia, e EC50, a potência.
os receptores estão ocupados pelo fármaco. Entretanto, alguns
fármacos são capazes de produzir uma resposta máxima quando
menos de 100% de seus receptores estão ocupados; os receptores remanescentes podem ser denominados receptores de
reserva. Esse conceito é discutido de modo mais detalhado
adiante. Observe mais uma vez que a curva de dose–resposta graduada da Fig. 2.2 exibe uma estreita semelhança com a
curva de ligação fármaco–receptor da Fig. 2.1, em que a Kd é
substituída pela EC50 e Ro é substituído por Emáx..
RELAÇÕES DE DOSE–RESPOSTA QUANTAIS
A relação de dose–resposta quantal representa graficamente
a fração da população que responde a determinada dose de
um fármaco como função da dose deste fármaco. As relações
de dose–resposta quantais descrevem as concentrações de um
fármaco que produzem determinado efeito numa população.
Farmacodinâmica
% Cumulativa exibindo
% de indivíduos que respondem
Efeito terapêutico
Efeito tóxico
Efeito letal
100
50
Efeito
terapêutico
% da dose necessária
para obter
Efeito tóxico
Efeito letal
|
21
cognatos. Um fármaco que, através de sua ligação a seu receptor, favorece a conformação ativa deste receptor é denominado
agonista; por outro lado, um fármaco que impede a ativação do
receptor pelo agonista é designado como antagonista. Alguns
fármacos não se enquadram exatamente dentro dessa definição
simples de agonista e antagonista; esses fármacos incluem os
agonistas parciais e os agonistas inversos. As seções que
se seguem descrevem essas classificações farmacológicas de
maneira mais detalhada.
AGONISTAS
0
ED50
TD50
LD50
Dose
Fig. 2.3 Curvas de dose–resposta quantais. As curvas de dose–resposta
quantais demonstram o efeito médio de um fármaco, como função de sua
concentração, em determinada população de indivíduos. Tipicamente, os
indivíduos são observados quanto à presença ou ausência de uma resposta
(por exemplo, sono ou ausência de sono) e, a seguir, o resultado obtido
é utilizado para representar graficamente a percentagem de indivíduos que
respondem a cada dose do fármaco. As relações de dose–resposta quantais
são úteis para prever os efeitos de um fármaco quando administrado a uma
população de indivíduos, bem como para determinar as doses tóxicas e as
doses letais dentro de uma população. Essas doses são denominadas ED 50
(dose em que 50% dos indivíduos apresentam uma resposta terapêutica a um
fármaco), TD50 (dose em que 50% dos indivíduos exibem uma resposta tóxica)
e LD50 (dose em que 50% dos indivíduos morrem). Observe que a ED50 é a
dose em que 50% dos indivíduos respondem a um fármaco, enquanto a EC 50
(conforme descrito na figura anterior) é a dose em que um fármaco produz
metade do efeito máximo em um indivíduo.
A Fig. 2.3 fornece um exemplo de curvas de dose–resposta
quantais. Devido a diferenças nas respostas biológicas entre
indivíduos, os efeitos de um fármaco são observados ao longo
de uma faixa de doses. As respostas são definidas em termos de
presentes ou ausentes (isto é, quantais, e não graduadas). Parâmetros finais, como “sono/sem sono” ou “estar vivo dentro de
12 meses/não estar vivo dentro de 12 meses” são exemplos de
respostas quantais; em contrapartida, as relações de dose–resposta graduadas são geradas utilizando respostas de grandeza
escalar, como mudança na pressão arterial ou na freqüência
cardíaca. O objetivo é generalizar um resultado para uma população, mais do que examinar o efeito graduado de diferentes
doses do fármaco sobre um indivíduo. Os tipos de respostas
que podem ser examinados com a relação de dose–resposta
quantal incluem a efetividade (efeito terapêutico), a toxicidade
(efeito adverso) e a letalidade (efeito letal). As doses que produzem essas respostas em 50% de uma população são conhecidas como dose efetiva mediana (ED50), dose tóxica mediana
(TD50) e dose letal mediana (LD50), respectivamente.
Um agonista é uma molécula que se liga a um receptor e o
estabiliza numa determinada conformação (habitualmente na
conformação ativa). Quando ligado por um agonista, um receptor típico tem mais tendência a encontrar-se na sua conformação
ativa do que na sua conformação inativa. Dependendo do receptor, os agonistas podem ser fármacos ou ligantes endógenos. A
Equação 2.6 fornece um modelo conveniente para compreender
a relação entre ligação do agonista e ativação do receptor:
D+ R
D + R*
DR
DR *
Equação 2.6
onde D e R são as concentrações do fármaco e do receptor
não-ligados (livres), respectivamente, DR é a concentração do
complexo agonista–receptor, e R* indica a conformação ativa
do receptor. Para a maioria dos pacientes e dos agonistas, R* e
DR são espécies instáveis que têm apenas uma existência breve,
sendo quantitativamente insignificantes em comparação com R
e DR*. Por conseguinte, na maioria dos casos, a Equação 2.6
é simplificada para
D+R
DR*
Equação 2.7
INTERAÇÕES FÁRMACO–RECEPTOR
Observe que a Equação 2.7 é idêntica à Equação 2.1, que foi
utilizada para análise da ligação fármaco–receptor. Isso sugere que, para a maioria dos receptores, a ligação do agonista
é proporcional à ativação do receptor. Todavia, alguns receptores apresentam estabilidade limitada nas conformações R*
e/ou DR; nesses casos, é preciso reexaminar a Equação 2.6
(ver adiante).
A Equação 2.6 também pode ser utilizada para ilustrar
quantitativamente os conceitos de potência e eficácia. Conforme assinalado anteriormente, a potência é a concentração
de agonista necessária para produzir metade do efeito máximo,
enquanto a eficácia é o efeito máximo do agonista. Admitindo
que um receptor não esteja ativo, a não ser que esteja ligado
a um fármaco (isto é, R* é insignificante em comparação com
DR*), a Equação 2.8 fornece uma descrição quantitativa da
potência e da eficácia:
kα
kligado
Equação 2.8
D+ R
DR
DR *
klivre
kβ
Muitos receptores de fármacos podem ser categorizados dentro de dois estados de conformação, que estão em equilíbrio
reversível entre si. Esses dois estados são denominados estado
ativo e estado inativo. Muitos fármacos atuam como ligantes
desses receptores e afetam a probabilidade de o receptor encontrar-se preferencialmente em uma dessas duas conformações.
As propriedades farmacológicas dos fármacos baseiam-se, com
freqüência, em seus efeitos sobre o estado de seus receptores
Nesta equação, k� é a constante de velocidade de ativação
do receptor, e k� é a constante de velocidade de desativação do
receptor. Essa equação demonstra a relação entre a potência (Kd
= klivre /kligado) e a ligação do agonista (D + R � DR), bem como
a relação entre a eficácia (k�/k�) e a mudança de conformação
necessária para a ativação do receptor (DR � DR*). Essas
relações são intuitivas se considerarmos que os fármacos mais
potentes são aqueles que possuem maior afinidade pelos seus
Potência
Eficácia
22
|
Capítulo Dois
receptores (Kd mais baixa), enquanto os fármacos mais eficazes
são aqueles que produzem ativação de uma maior proporção
de receptores.
gonistas sem receptores também são examinados de modo
sucinto.
Antagonistas Competitivos dos Receptores
ANTAGONISTAS
Um antagonista é uma molécula que inibe a ação de um agonista, mas que não exerce nenhum efeito na ausência do agonista. A Fig. 2.4 fornece uma abordagem para a classificação
dos vários tipos de antagonistas. Os antagonistas podem ser
divididos em antagonistas de receptores e antagonistas sem
receptores. O antagonista de receptor liga-se ao sítio ativo
(sítio de ligação do agonista) ou a um sítio alostérico de um
receptor. A ligação do antagonista ao sítio ativo impede a ligação do agonista ao receptor, enquanto a ligação do antagonista
a um sítio alostérico altera a Kd para a ligação do agonista ou
impede a mudança de conformação necessária para a ativação
do receptor. Os antagonistas de receptores também podem ser
divididos em antagonistas reversíveis e irreversíveis, isto é,
antagonistas que se ligam a seus receptores de modo reversível
e antagonistas que se ligam irreversivelmente. A Fig. 2.5 ilustra
os efeitos gerais desses tipos de antagonistas sobre a ligação dos
agonistas; as seções que se seguem apresentam uma descrição
mais detalhada desse tópico.
O antagonista sem receptores não se liga ao receptor do
agonista; entretanto, inibe a capacidade do agonista de iniciar
uma resposta. Em nível molecular, essa inibição pode ocorrer
através da inibição direta do agonista (por exemplo, utilizando
anticorpos), através da inibição de uma molécula localizada distalmente na via de ativação, ou através da ativação de uma via
que se opõe à ação do agonista. Os antagonistas sem receptores
podem ser classificados em antagonistas químicos e antagonistas fisiológicos. Os antagonistas químicos inativam o agonista
antes de ele ter a oportunidade de atuar (por exemplo, através de
neutralização química); os antagonistas fisiológicos produzem
um efeito fisiológico oposto àquele induzido pelo agonista.
A seção que se segue trata dos antagonistas competitivos
dos receptores e dos antagonistas não-competitivos. Os anta-
Um antagonista competitivo liga-se reversivelmente ao sítio
de um receptor. Ao contrário do agonista, que também se liga
ao sítio ativo do receptor, o antagonista competitivo não estabiliza a conformação necessária para a ativação do receptor.
Por conseguinte, o antagonista bloqueia a ligação do agonista a
seu receptor, enquanto mantém o receptor em sua conformação
inativa. A Equação 2.9 é uma modificação da Equação 2.7, que
incorpora o efeito de um antagonista competitivo (A).
AR
A+D+R
DR*
Equação 2.9
Nesta equação, uma fração das moléculas livres do receptor (R)
é incapaz de formar um complexo fármaco (agonista)–receptor
(DR*), visto que a ligação do receptor ao antagonista resulta
na formação de um complexo antagonista–receptor (AR). Com
efeito, a formação do complexo AR estabelece uma segunda
reação de equilíbrio, que compete com o equilíbrio da ligação
agonista–receptor. Observe que o complexo AR é incapaz de
sofrer uma mudança de conformação para o estado ativo (R*)
do receptor.
A análise quantitativa leva à seguinte equação para a ligação
de um agonista (D) ao receptor, na presença de um antagonista
competitivo (A):
[ DR]
[ D]
=
[ A] 
R
[ o]
[ D] + K d 1 +

KA 
Equação 2.10
A Equação 2.10 assemelha-se à Equação 2.4, exceto que a
Kd efetiva foi aumentada por um fator de (1 + [A]/KA), onde
KA é a constante de dissociação para a ligação do antagonista
ao receptor (isto é, KA = [A][R]/[AR]). Como o aumento da
Kd equivale a uma diminuição de potência, a presença de um
antagonista competitivo (A) diminui a potência de um agonista
Antagonistas
Antagonistas
dos receptores
Ligação ao
sítio ativo
Reversível
Irreversível
Antagonista
competitivo
Antagonista
não-competitivo
no sítio ativo
Antagonistas
sem receptores
Ligação
alostérica
Reversível
Irreversível
Antagonista
alostérico
não-competitivo
Antagonista
químico
Antagonista
fisiológico
Fig. 2.4 Classificação dos antagonistas. Os antagonistas podem ser categorizados com base na sua ligação a um sítio do receptor para o agonista (antagonistas
dos receptores) ou interrupção da sinalização do complexo agonista–receptor por outros meios (antagonistas sem receptores). Os antagonistas dos receptores
podem ligar-se ao sítio do agonista (ativo) ou a um sítio alostérico no receptor; em ambos os casos, eles não afetam a atividade basal do receptor (isto é, a
atividade do receptor na ausência do agonista). Os antagonistas dos receptores no sítio do agonista (ativo) impedem a ligação do agonista ao receptor. Quando
o agonista compete com o ligante pela sua ligação ao sítio agonista, é denominado antagonista competitivo; a presença de altas concentrações do agonista
pode superar o antagonismo competitivo. Os antagonistas não-competitivos no sítio do agonista ligam-se de modo covalente ou com afinidade muito alta
ao sítio agonista, de modo que até mesmo concentrações elevadas do agonista são incapazes de ativar o receptor. Os antagonistas dos receptores em sítio
alostérico ligam-se ao receptor em um local distinto do sítio agonista. Não competem diretamente com o agonista pela ligação ao receptor, porém alteram a
Kd para a ligação do agonista ou inibem a resposta do receptor à ligação do agonista. Em geral, a presença de concentrações elevadas do agonista não é capaz
de reverter o efeito de um antagonista alostérico. Os antagonistas sem receptores são divididos em duas categorias. Os antagonistas químicos seqüestram o
agonista e, por conseguinte, impedem a interação do agonista com o receptor. Os antagonistas fisiológicos induzem uma resposta fisiológica oposta àquela do
agonista, porém através de um mecanismo molecular que não envolve o receptor do agonista.
Farmacodinâmica
|
23
Agonista
Sítio de ligação
do agonista
A
Agonista
Agonista
Antagonista
competitivo
Sítio de ligação
alostérico do
antagonista B
C
Receptor não-ligado
Ligação do agonista
D
Ligação do antagonista
competitivo
Antagonista
não-competitivo
Ligação do antagonista
não-competitivo
Fig. 2.5 Tipos de antagonistas dos receptores. Ilustração esquemática das diferenças entre antagonistas nos sítios agonista (ativo) e alostérico. A. O receptor
inativo não-ligado. B. O receptor ativado pelo agonista. Observe a mudança de conformação induzida no receptor pela ligação do agonista, por exemplo, a
abertura de um canal iônico transmembrana. C. Os antagonistas no sítio agonista ligam-se ao sítio agonista do receptor, porém não ativam o receptor; esses
agentes bloqueiam a ligação do agonista ao receptor. D. Os antagonistas alostéricos ligam-se a um sítio alostérico (distinto do sítio agonista) e, por conseguinte,
impedem a ativação do receptor, mesmo se o agonista estiver ligado ao receptor.
(D) por um fator de (1 + [A]/KA). Apesar de a potência de um
agonista diminuir à medida que aumenta a concentração do
antagonista competitivo, a eficácia do agonista não é afetada.
Isso se deve ao fato de que a concentração do agonista [D] pode
ser aumentada para contrapor-se ao antagonista (“superá-lo”),
“eliminando” ou revertendo, assim, o efeito do antagonista.
A Fig. 2.6A mostra o efeito de um antagonista competitivo
A Antagonista competitivo
% de resposta
100
Agonista isolado
Agonista + Antagonista
50
Antagonista isolado
0
Antagonistas Não-Competitivos dos Receptores
B Antagonista não-competitivo
% de resposta
100
Agonista isolado
Agonista + Antagonista
50
0
sobre a relação dose de antagonista–resposta. Observe que o
antagonista competitivo tem o efeito de desviar a curva de dose
de agonista–resposta para a direita, causando uma redução de
potência do agonista, porém mantendo a sua eficácia.
A pravastatina, o fármaco utilizado no caso descrito no
início do capítulo para reduzir o nível de colesterol do Almirante, fornece um exemplo de um antagonista competitivo. A
pravastatina é um membro da classe de inibidores da HMG CoA
redutase (estatinas) de fármacos hipolipêmicos. A HMG CoA
redutase é uma enzima que catalisa a redução da HMG CoA,
que constitui a etapa que limita a velocidade na biossíntese do
colesterol. A semelhança entre as estruturas químicas das estatinas e a HMG CoA permite a ligação da molécula de estatina ao
sítio ativo da HMG CoA redutase, impedindo, assim, a ligação
da HMG CoA. A inibição da HMG CoA redutase diminui a
síntese endógena de colesterol e, portanto, diminui os níveis de
colesterol do paciente. Essa inibição é reversível, visto que não
há formação de ligações covalentes entre a estatina e a enzima.
Para uma discussão mais detalhada da pravastatina e de outros
inibidores da HMG CoA redutase, ver o Cap. 23.
Antagonista isolado
Concentração de agonista ou de antagonista
Fig. 2.6 Efeitos dos antagonistas sobre a relação de dose agonista–
resposta. Os antagonistas competitivos e não-competitivos possuem diferentes
efeitos sobre a potência (a concentração do agonista que produz metade
da resposta máxima) e a eficácia (a resposta máxima a um agonista). A.
Um antagonista competitivo diminui a potência de um agonista, sem afetar
a sua eficácia. B. Um antagonista não-competitivo reduz a eficácia de um
agonista. Conforme ilustrado aqui, a maioria das antagonistas não-competitivos
alostéricos não afeta a potência do agonista.
Os antagonistas não-competitivos podem ligar-se ao sítio ativo ou a um sítio alostérico de um receptor (Fig. 2.4). O antagonista não-competitivo que se liga ao sítio ativo de um receptor
pode fazê-lo de modo covalente ou com afinidade muito alta;
em ambos os casos, a ligação é efetivamente irreversível. Como
um antagonista irreversivelmente ligado ao sítio ativo não pode
ser “superado”, mesmo com altas concentrações do agonista,
esse antagonista exibe antagonismo não-competitivo.
Um antagonista alostérico não-competitivo atua ao impedir
a ativação do receptor, mesmo quando o agonista está ligado ao sítio ativo. O antagonista alostérico exibe antagonismo
não-competitivo, independentemente da reversibilidade de sua
ligação, visto que esse tipo de antagonista não atua ao competir
com o agonista pela sua ligação ao sítio ativo, mas ao impedir
a ativação do receptor. Entretanto, a reversibilidade da ligação
do antagonista é importante, visto que o efeito de um antagonista irreversível não diminui, mesmo quando o fármaco livre
(não-ligado) é eliminado do organismo, enquanto o efeito de
um antagonista reversível pode ser “eliminado” com o decorrer
do tempo, à medida que se dissocia do receptor (ver Equação
2.9).
Um receptor ao qual está ligado um antagonista não-competitivo não pode mais responder à ligação de um agonista.
|
Capítulo Dois
Por conseguinte, a resposta máxima (eficácia) do agonista é
reduzida. Uma diferença característica entre antagonistas competitivos e não-competitivos reside no fato de que os antagonistas competitivos reduzem a potência do agonista, enquanto
os antagonistas não-competitivos diminuem a eficácia do agonista. Essa diferença pode ser explicada com base no fato de
que um antagonista competitivo compete continuamente pela
sua ligação ao receptor, diminuindo efetivamente a afinidade do
receptor pelo seu agonista, sem limitar o número de receptores
disponíveis. Em contrapartida, um antagonista não-competitivo
remove receptores funcionais do sistema, limitando, assim, o
número de receptores disponíveis. As Figs. 2.6A e 2.6B comparam os efeitos de antagonistas competitivos e não-competitivos
sobre a relação dose de agonista–resposta.
A aspirina é um exemplo de antagonista não-competitivo.
Esse agente acetila irreversivelmente a ciclo-oxigenase, a enzima responsável pela produção de tromboxano A2 nas plaquetas. Na ausência de geração de tromboxano A2, ocorre inibição
da agregação plaquetária. Como a inibição é irreversível, e as
plaquetas são incapazes de sintetizar novas moléculas de ciclooxigenase, os efeitos de uma dose única de aspirina persistem
por 7 a 10 dias (o tempo necessário para a produção de novas
plaquetas pela medula óssea), embora o fármaco livre seja
depurado muito mais rapidamente do organismo.
Antagonistas Sem Receptores
Os antagonistas sem receptores podem ser classificados em
antagonistas químicos e antagonistas fisiológicos. Um antagonista químico inativa o agonista específico ao modificá-lo ou
seqüestrá-lo, de modo que o agonista não é mais capaz de ligarse ao receptor e de ativá-lo. A protamina é um exemplo de
antagonista químico; essa proteína básica liga-se estequiometricamente à classe de anticoagulantes da heparina, inativando
esses agentes (ver Cap. 22). Devido a esse antagonismo químico, a protamina pode ser utilizada para interromper rapidamente
os efeitos da heparina.
Um antagonista fisiológico ativa ou bloqueia mais comumente um receptor que medeia uma resposta fisiologicamente
oposta àquela do receptor do agonista. Assim, por exemplo,
no tratamento do hipertireoidismo, os antagonistas �-adrenérgicos são utilizados como antagonistas fisiológicos para
reverter o efeito de taquicardia do hormônio tireoidiano endógeno. Embora o hormônio tireoidiano não produza seu efeito
de taquicardia através de estimulação �-adrenérgica, o bloqueio
da estimulação �-adrenérgica pode, entretanto, aliviar a taquicardia causada pelo hipertireoidismo (ver Caps. 9 e 26).
AGONISTAS PARCIAIS
Um agonista parcial é uma molécula que se liga a um receptor
em seu sítio ativo, mas que só produz uma resposta parcial,
mesmo quando todos os receptores estão ocupados (ligados)
pelo agonista. A Fig. 2.7 mostra uma série de curvas de dose–
resposta para vários agonistas integrais e parciais. Cada agonista atua através de sua ligação ao mesmo sítio no receptor
muscarínico de acetilcolina (ACh). Observe que o butil trimetilamônio (TMA) não é apenas mais potente do que os derivados
de cadeia mais longa na estimulação da contração muscular,
como também mais eficaz do que alguns dos derivados (por
exemplo, as formas heptila e octila) na produção de uma maior
resposta máxima. Por esse motivo, o butil TMA é um agonista
integral no receptor muscarínico de ACh, enquanto o derivado
octila é um agonista parcial nesse receptor.
100
Butila
Hexila
% de contração
24
Heptila
50
0
10-7
Octila
10-6
10-5
10-4
10-3
[D] (Molar)
Fig. 2.7 Curvas de dose–resposta de agonistas integrais e parciais. Existem
muitos casos em que fármacos que atuam no sítio agonista do mesmo receptor
produzem diferentes efeitos máximos. Por exemplo, vários derivados alquila do
trimetilamônio estimulam, todos eles, os receptores muscarínicos de acetilcolina
(ACh), causando contração muscular no intestino, porém produzem respostas
máximas diferentes, mesmo quando todos os receptores estão ocupados.
Nessa figura, os derivados butil e hexil trimetilamônio são agonistas integrais
— apesar de terem potências diferentes, ambos são capazes de produzir uma
resposta máxima. Os agonistas que produzem apenas uma resposta parcial,
como os derivados heptila e octila, são denominados agonistas parciais.
Observe que as curvas de dose–resposta dos agonistas parciais formam um
platô em valores abaixo daqueles dos agonistas integrais. A ACh atua como
agonista integral nesse sistema (não ilustrada).
Como os agonistas parciais e os agonistas integrais ligam-se
ao mesmo sítio no receptor, o agonista parcial pode reduzir a
resposta produzida por um agonista integral. Dessa maneira, o
agonista parcial pode atuar como antagonista competitivo. Por
essa razão, os agonistas parciais são algumas vezes denominados “antagonistas parciais” ou até mesmo “agonistas-antagonistas mistos”.
É interessante indagar como um agonista poderia produzir
uma resposta abaixo da máxima se um receptor só pode existir
no estado ativo ou inativo. Esta é uma área de pesquisa atual, para a qual foram aventadas diversas hipóteses. Podemos
lembrar que a Equação 2.6 foi simplificada na Equação 2.7
com base na pressuposição de que a R e a DR* são muito
mais estáveis do que a R* e a DR. Mas o que poderia ocorrer
se um fármaco (vamos chamá-lo de agonista parcial) pudesse
estabilizar a DR, bem como a DR*? Nesse caso, a adição do
agonista parcial resultaria na estabilização de alguns receptores
na forma DR e de alguns receptores na forma DR*. Com a
ocupação integral dos receptores, alguns receptores estariam no
estado ativo e outros no estado inativo, e a eficácia do fármaco
estaria reduzida em comparação com a de um agonista integral
(que estabiliza apenas DR*). Nessa formulação, um antagonista
puro liga-se preferencialmente ao estado inativo do receptor;
um agonista integral liga-se de preferência ao estado ativo do
receptor, e um agonista parcial liga-se com afinidade comparável aos estados tanto ativo quanto inativo do receptor.
Uma segunda hipótese formulada para a ação dos agonistas
parciais é a de que um receptor pode exibir múltiplas conformações DR*, cada uma com atividade intrínseca diferente. Dependendo das conformações particulares do receptor ligadas pelo
agonista, pode-se observar uma fração do efeito máximo possí-
Farmacodinâmica
vel quando um agonista parcial liga-se a 100% dos receptores.
Este pode ser o caso dos denominados moduladores seletivos
dos receptores de estrogênio (MSRE), como o raloxifeno e
o tamoxifeno (ver Cap. 28). O raloxifeno atua como agonista
parcial nos receptores de estrogênio presentes no osso e como
antagonista nos receptores de estrogênio na mama. A estrutura cristalina do raloxifeno ligado ao receptor de estrogênio,
quando comparada com a do estrogênio ligado ao receptor de
estrogênio, revela que a cadeia lateral do raloxifeno inibe o
alinhamento de uma hélice � do receptor de estrogênio no sítio
ativo (ver contracapa frente). Isso pode resultar em inibição de
alguns efeitos distais do receptor de estrogênio, enquanto outros
efeitos são mantidos. Em nível fisiológico, esse efeito seria
observado como atividade agonista parcial no osso.
Outro exemplo de agonista parcial é o pindolol, um fármaco
freqüentemente classificado como antagonista �-adrenérgico
(ver Cap. 9). Todavia, na realidade, o pindolol exibe propriedades de agonista parcial, e esse fármaco pode ter valor clínico em
virtude da resposta intermediária que ele produz. Embora a freqüência cardíaca e a pressão arterial em repouso não sejam tão
reduzidas pelo pindolol quanto por outros antagonistas �-adrenérgicos puros, o pindolol inibe de modo efetivo os aumentos
potencialmente perigosos da freqüência cardíaca e da pressão
arterial que de outro modo poderiam ocorrer com estimulação
simpática (por exemplo, exercício físico) em pacientes com
doença cardiovascular.
|
25
RECEPTORES DE RESERVA
Convém lembrar que, com base na pressuposição inicial sobre
a ligação fármaco–receptor, é necessária a ocupação de 100%
dos receptores para que um agonista exerça seu efeito máximo.
Agora, consideremos a possibilidade de que se possa obter uma
resposta máxima com uma ocupação de menos de 100% dos
receptores. A Fig. 2.8 mostra um exemplo de uma curva de
ligação fármaco–receptor e de uma curva de dose–resposta
que ilustram essa situação. Neste exemplo, obtém-se um efeito
máximo numa dose de agonista mais baixa do que a necessária
para saturação dos receptores, isto é, a EC50 é menor do que a
Kd para esse sistema. Esse tipo de discrepância entre a curva de
ligação fármaco–receptor e a curva de dose–resposta significa
a presença de receptores de reserva. Acredita-se que pelo
menos dois mecanismos moleculares sejam responsáveis pelo
A Curva de ligação fármaco–receptor
1,0
[DR]
[R0]
0,5
AGONISTAS INVERSOS
A ação dos agonistas inversos pode ser compreendida se considerarmos novamente a Equação 2.6. Conforme assinalado anteriormente, em alguns casos, os receptores podem apresentar uma
estabilidade inerente no estado R*. Nessa circunstância, existe
uma atividade intrínseca (“tônus”) do sistema receptor, mesmo
na ausência de um ligante endógeno ou de um agonista exógeno
administrado. Um agonista inverso atua de modo a abolir essa
atividade intrínseca (constitutiva) do receptor livre (não-ocupado). Os agonistas inversos podem atuar através de sua ligação
ao receptor na forma DR (inativa) e de sua estabilização. Isso
tem o efeito de desativar os receptores que se encontravam na
forma R* na ausência do fármaco. A importância fisiológica dos
receptores que possuem estabilidade inerente no estado R* está
sendo atualmente investigada, e os receptores com mutações
que os tornam constitutivamente ativos (por exemplo, BCRAbl e EGFR tirosinocinases) estão se tornando alvos interessantes na abordagem da quimioterapia do câncer com agonistas
inversos (ver Cap. 38).
Consideremos as semelhanças e as diferenças entre as ações
dos agonistas inversos e dos antagonistas competitivos. Ambos
os tipos de fármacos atuam no sentido de reduzir a atividade
de um receptor. Na presença de agonista integral, tanto os antagonistas competitivos quanto os agonistas inversos têm, como
ação, reduzir a potência do agonista. Entretanto, convém lembrar que um antagonista competitivo não exerce nenhum efeito
na ausência do agonista, enquanto um agonista inverso desativa
os receptores que estão constitutivamente ativos na ausência do
agonista. Se utilizarmos as Equações 2.6 até 2.9 como modelos, esses conceitos podem ser resumidos da seguinte maneira:
os agonistas integrais estabilizam DR*, os agonistas parciais
estabilizam tanto DR quanto DR* (ou formas alternadas de
DR*), os agonistas inversos estabilizam DR, e os antagonistas
competitivos “estabilizam” R (ou AR) ao impedir a ligação dos
agonistas integrais, parciais e inversos ao receptor.
0
Kd
B Curva de dose–resposta
1,0
E
Emáx.
0,5
0
EC50
Kd
[D]
Fig. 2.8 Comparação entre uma curva de ligação fármaco–receptor e uma
curva de dose–resposta na presença de receptores de reserva. Na ausência
de receptores de reserva, existe freqüentemente uma estreita correlação entre
a curva de ligação fármaco–receptor e a curva de dose–resposta — a ligação
de uma quantidade adicional do fármaco ao receptor produz aumento da
resposta, e a EC50 é aproximadamente igual à Kd. Entretanto, em situações
com presença de receptores de reserva, verifica-se metade da resposta
máxima quando menos da metade de todos os receptores está ocupada (o
termo reserva implica que não há necessidade de ocupação de todos os
receptores com o fármaco para produzir uma resposta integral). A. Curva de
ligação fármaco–receptor. B. Curva de dose–resposta do mesmo fármaco, na
presença de receptores de reserva. Observe que a resposta máxima ocorre
numa concentração de agonista mais baixa do que a ligação máxima, e EC50
< Kd. Essas duas relações confirmam a presença de receptores de reserva. D é
o fármaco, R é o receptor e [DR]/[Ro] é a ocupação fracionária do receptor. E
é a resposta (efeito), Emáx. é a resposta máxima (eficácia) e E/Emáx. é a resposta
fracionária. EC50 é a potência, e Kd é a constante de dissociação em equilíbrio
para a ligação fármaco–receptor.
26
|
Capítulo Dois
fenômeno do receptor de reserva. Em primeiro lugar, é possível
que o receptor permaneça ativado após a saída do agonista,
permitindo a ativação de vários receptores por uma molécula
de agonista. Em segundo lugar, as vias de sinalização celulares
descritas no Cap. 1 poderiam propiciar uma amplificação significativa de um sinal relativamente pequeno, e a ativação de
apenas alguns receptores poderia ser suficiente para produzir
uma resposta máxima. Este último mecanismo aplica-se, por
exemplo, no caso de muitos receptores acoplados à proteína
G; a ativação de uma única molécula de G�s pode estimular a
adenilil ciclase a catalisar a formação de dúzias de moléculas
de cAMP.
A presença de receptores de reserva altera o efeito de um
antagonista não-competitivo sobre o sistema. Na presença de
baixas concentrações do antagonista, o antagonista não-competitivo liga-se a receptores que não são necessários para produzir
uma resposta máxima; por conseguinte, não há diminuição da
eficácia do agonista. Entretanto, a potência do agonista é afetada, visto que a potência é proporcional à fração de receptores
disponíveis que devem estar ocupados para produzir 50% da
resposta. O antagonista não-competitivo reduz o número de
receptores disponíveis, aumentando, assim, a fração de receptores que precisam estar ligados em qualquer concentração do
agonista para produzir a mesma resposta. Na presença de altas
concentrações do antagonista, o antagonista não-competitivo
liga-se não apenas aos receptores de “reserva”, mas também
aos receptores necessários para produzir a resposta máxima,
e ocorre uma redução tanto da eficácia quanto da potência do
agonista. A Fig. 2.9 ilustra esse conceito.
CONCEITOS EM TERAPIA
ÍNDICE TERAPÊUTICO E JANELA TERAPÊUTICA
A janela terapêutica é a faixa de doses (concentrações) de
um fármaco que produz uma resposta terapêutica, sem efeitos
adversos inaceitáveis (toxicidade), numa população de pacientes. Para fármacos que possuem uma pequena janela terapêutica, é preciso efetuar uma estreita monitorização dos níveis
plasmáticos do fármaco para manter uma dose efetiva, sem
ultrapassar o nível passível de provocar toxicidade. O próximo capítulo irá discutir algumas das técnicas empregadas em
terapia clínica para manter as concentrações plasmáticas dos
fármacos dentro da janela terapêutica.
A janela terapêutica pode ser quantificada pelo índice terapêutico (IT) (algumas vezes denominado relação terapêutica), que costuma ser definida como:
TD50
Equação 2.11
ED50
onde TD50 é a dose do fármaco que produz uma resposta tóxica
em 50% da população, e ED50 é a dose do fármaco terapeuticamente efetiva em 50% da população. O IT fornece um único número que quantifica a margem de segurança relativa de
um fármaco numa população. Um alto valor de IT representa
uma janela terapêutica grande (ou “larga”) (por exemplo, uma
diferença de mil vezes entre as doses terapêuticas e tóxicas),
enquanto um IT pequeno indica uma janela terapêutica pequena
(ou “estreita”) (por exemplo, uma diferença de duas vezes entre
as doses terapêuticas e tóxicas).
O potencial de toxicidade associado ao uso da heparina e
do tPA no caso apresentado no início deste capítulo é indiÍndice terapêutico (IT) =
1,0
Agonista apenas
E
0,5
Emáx.
Agonista + concentrações
crescentes de antagonista
não-competitivo
0
[D]
Fig. 2.9 Efeito de um antagonista não-competitivo sobre a curva de
dose de agonista–resposta na presença de receptores de reserva. Em
um sistema com ausência de receptores de reserva, um antagonista nãocompetitivo produz uma diminuição da eficácia em todas as concentrações
do antagonista (ver Fig. 2.6B). Entretanto, em um sistema com receptores de
reserva, a potência encontra-se diminuída, porém a eficácia não é afetada
em baixas concentrações do antagonista, visto que um número suficiente de
receptores desocupados está disponível para gerar uma resposta máxima. À
medida que concentrações crescentes do antagonista ligam-se de modo nãocompetitivo a um número cada vez maior de receptores, o antagonista acaba
ocupando todos os receptores de “reserva”, e verifica-se também uma redução
da eficácia.
cado pelos baixos IT desses fármacos. Por exemplo, a dose
de heparina capaz de provocar sangramento significativo em
um paciente é, com freqüência, menos de duas vezes a dose
necessária para obter um efeito terapêutico; por conseguinte,
a heparina pode ser definida como um fármaco de índice terapêutico inferior a dois. Por esse motivo, nos pacientes tratados
com heparina, é preciso determinar o TTP, um marcador da
cascata da coagulação, a cada 8 a 12 horas. O elevado IT da
aspirina indica sua relativa segurança. Observe que o efeito
farmacológico da heparina foi monitorado periodicamente no
caso descrito, enquanto a aspirina pôde ser administrada sem
a necessidade de monitorar seus níveis plasmáticos.
� Conclusão e Perspectivas Futuras
A farmacodinâmica é o estudo quantitativo dos efeitos dos
fármacos sobre o organismo. Foram desenvolvidas várias ferramentas para comparar a eficácia e a potência dos fármacos,
incluindo as relações de dose–resposta graduadas e quantais.
A relação de dose–resposta graduada é utilizada para examinar
os efeitos de várias doses de um fármaco sobre um indivíduo,
enquanto a relação de dose–resposta quantal é utilizada para
examinar os efeitos de várias doses de um fármaco sobre uma
população. A janela terapêutica e o índice terapêutico são utilizados para comparar as concentrações de fármacos que produzem efeitos terapêuticos e efeitos tóxicos (adversos).
No estudo da farmacodinâmica, os fármacos podem ser divididos em duas classes gerais — agonistas e antagonistas. A
maioria dos agonistas permite a manutenção da conformação
de um receptor no estado ativo, enquanto os antagonistas impedem a ativação do receptor pelos agonistas. Os antagonistas são
ainda classificados de acordo com a localização molecular de
seu efeito (isto é, receptores ou não-receptores), o sítio onde se
ligam ao receptor (isto é, sítio ativo ou sítio alostérico) e o modo
Farmacodinâmica
|
27
QUADRO 2.1 Resumo da Ação dos Agonistas e Antagonistas
CLASSES DE AGONISTAS
CLASSE DE AGONISTAS
AÇÃO
Agonista integral
Ativa o receptor com eficácia máxima
Agonista parcial
Ativa o receptor, mas não com eficácia máxima
Agonista inverso
Inativa o receptor constitutivamente ativo
CLASSES DE ANTAGONISTAS
CLASSE DE ANTAGONISTAS
EFEITOS SOBRE
A POTÊNCIA DO
AGONISTA
EFEITOS SOBRE
A EFICÁCIA DO
AGONISTA
Antagonista competitivo
Sim
Não
Liga-se reversivelmente ao sítio ativo do receptor;
compete com a ligação do agonista a esse sítio
Antagonista não-competitivo no sítio
ativo
Não
Sim
Liga-se irreversivelmente ao sítio ativo do
receptor; impede a ligação do agonista a esse sítio
Antagonista alostérico não-competitivo
Não
Sim
Liga-se de modo reversível ou irreversível a
um sítio diferente do sítio ativo do receptor;
altera a Kd para a ligação do agonista ou impede
a mudança de conformação necessária para a
ativação do receptor pelo agonista
de sua ligação ao receptor (isto é, reversível ou irreversível). O
Quadro 2.1 fornece um resumo dos vários tipos de agonistas e
antagonistas descritos neste capítulo.
As informações apresentadas neste capítulo serão reiteradamente utilizadas neste livro, bem como por cada profissional de
saúde em sua prática clínica. O conhecimento prático da farmacodinâmica é essencial em todos os casos em que se efetua
uma comparação entre fármacos com base na sua potência ou
eficácia, ou nos casos em que é necessário estabelecer a dose
apropriada de um fármaco para um paciente específico.
AÇÃO
� Leituras Sugeridas
Berg JM, Tymoczko JL, Stryer L. Biochemistry. 6th ed. New York:
WH Freeman and Company; 2006. (Discute a base estrutural das
interações proteína-proteína.)
Leff P. The two-state model of receptor activation. Trends Pharmacol Sci
1995;16:89–97. (Fornece a base teórica para a Equação 2.6; discute
o tratamento quantitativo das interações fármaco–receptor.)
Pratt WB, Taylor P, eds. Principles of drug action: the basis of pharmacology. 3rd ed. New York: Churchill Livingstone; 1990. (Contém
uma discussão detalhada de farmacodinâmica.)