Resolução Exercícios Cálculo III 1) Calcular onde : a) e R é o

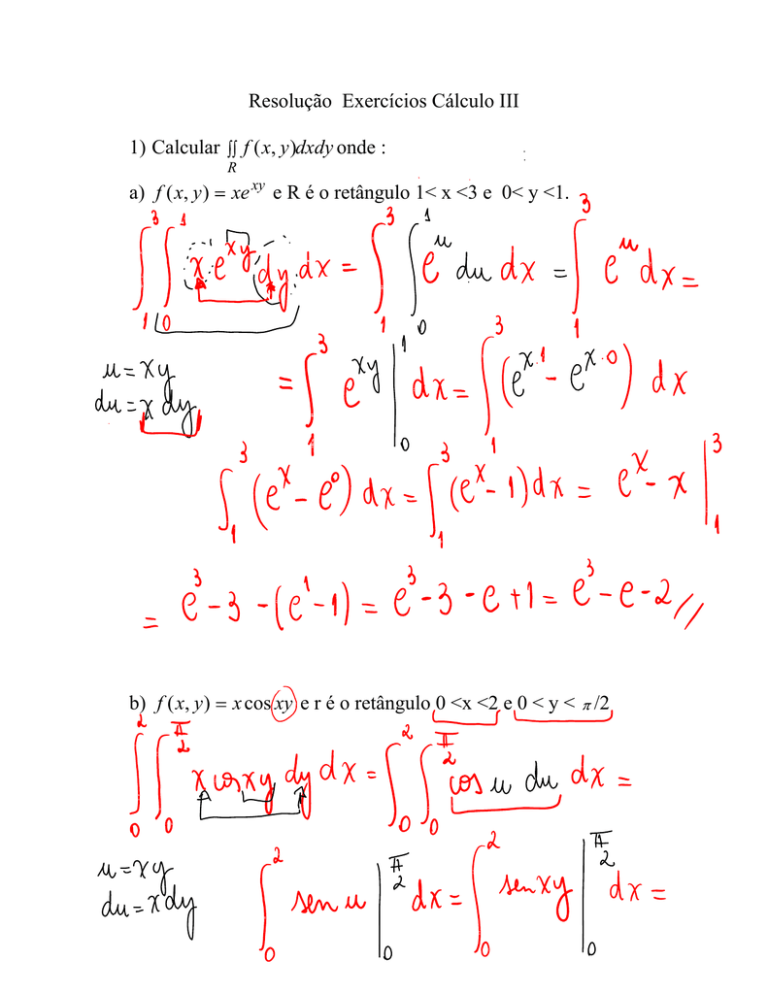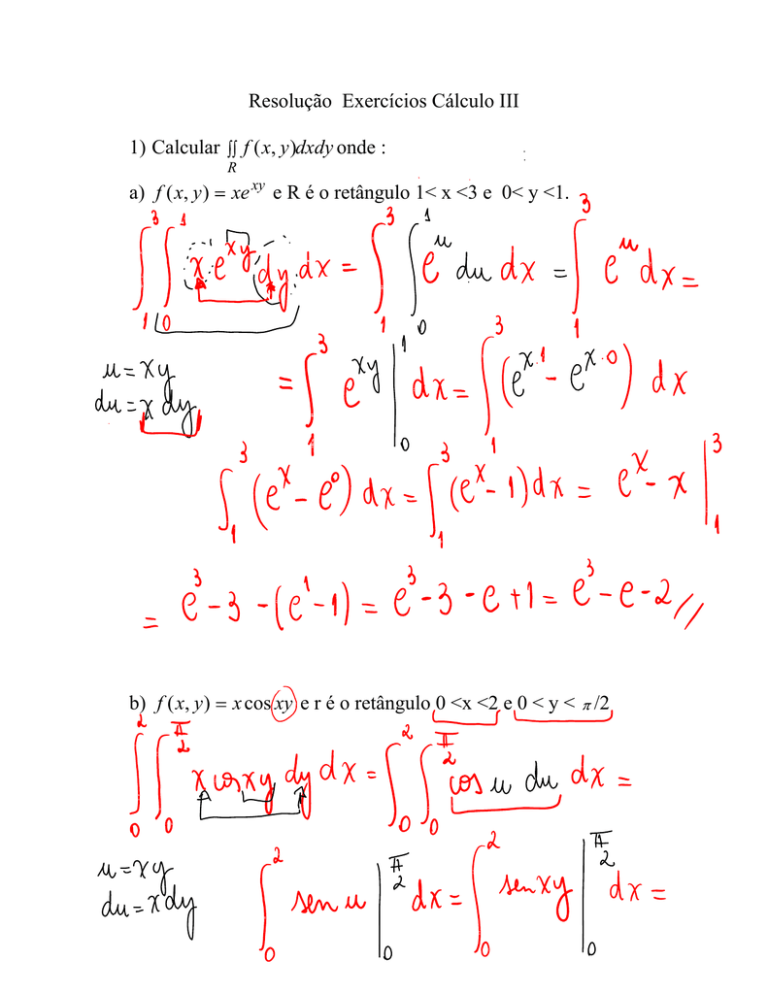
Resolução Exercícios Cálculo III
1) Calcular
f ( x, y )dxdy onde :
R
a) f ( x, y )
xe xy e R é o retângulo 1< x <3 e 0< y <1.
b) f ( x, y )
x cos xy e r é o retângulo 0 <x <2 e 0 < y < /2
2) Calcular as seguintes integrais
1 2x
a)
(2 x 4 y )dydx
0 x
2 y
b)
( xy 2
x)dxdy
0 y
3) Calcular
(8 x
R
e y = 4.
y )dxdy
onde R é a região delimitada por
y
x2
4) Calcular
onde r é a região delimitada por y = - x , y =
xdxdy
R
4x e
3
x
2
y
5
.
2
5)Calcular
senxsenydxdy ,
onde R é o retângulo
0
x
R
6) Calcular
ydxdy ,
2
,0
y
2
.
sendo R a região delimitada por x=0,
R
y2 1,
y=2 e y=-2.
7)Calcular ( x 2 y 2 )dxdy sendo R a região interna à circunferência
x
R
a circunferência.
8) Calcular, usando coordenadas polares, a integral
x
2
y
2
4y e x2
2 y externa
y2
x2
y 2 dxdy ,
R
sendo R a região delimitada por x y 1 e x y 9 .
9) Determinar a área da região R delimitada pelas curvas y x 3 , x
+ y = 2 e y = 0.
10) Determinar
dV , sendo T a região do primeiro octante
2
2
2
2
T
limitada por
x
4
11) Calcular
y2,
dV
y=z, x = 0 e z = 0.
, sendo T a coroa esférica delimitada por
T
e
12) Determine
x2
y2
z2
9
x2
y2
xydV
16 .
z2
, onde T é a região delimitada por y = 0 , x
T
= 0, z = 0 , z 4 x 2 e y + z =8.
13) Calcular o volume do sólido limitada acima da esfera
x 2 y 2 z 2 16 e abaixo pelo cone 3 z 2 x 2 y 2 .
14) Resolva o exercício anterior utilizando coordenadas esféricas.
15) Encontrar a integral
( x 2 y 2 ) 2 dxdxydz onde T é a região
T
delimitada pelo cilindro
x
2
y2
9
e pelos planos z=2 e z=4.