Integrais Múltiplos

Integrais Múltiplos
Matemática Aplicada
Artur Miguel Cruz
Escola Superior de Tecnologia
Instituto Politécnico de Setúbal
2014/2015 1
1
versão 10 de Outubro de 2015
Integrais Duplos
No cálculo integral a uma variável, o integral definido
Z b
f (x) dx
a
para uma função f : D ⊆ R → R não negativa é a área sob a curva y = f (x) desde x = a
até x = b.
O integral definido pode ser estendido a funções com mais de uma variável. O integral
duplo representa-se por
Z Z
f (x, y) dxdy
D
onde D é a região de integração no plano xOy. Para uma função f : D ⊆ R2 → R não
negativa, o integral duplo é o volume sob a superfı́cie z = f (x, y) na região D.
Uma região D ⊆ R2 diz-se decomponı́vel numa malha rectangular constituı́da por n
rectângulos Di (i = 1, . . . , n) se a união desses rectângulos é igual a D e a intersecção dos
conjuntos dos pontos interiores de Di dois a dois, é vazia. Seja Ai a área do rectângulo
Di .
2
Definição. Seja f : D ⊆ R2 → R uma função limitada e definida num conjunto
compacto (fechado e limitado) D ⊆ R2 . Diz-se que f é integrável à Riemann em
D se o limite
n
X
f (xi , yi ) Ai
lim
n→+∞
max Ai →0 i=1
existe e não depende da decomposição de D nem da escolha dos pontos arbitrários
(xi , yi ) ∈ Di ∩ D. O respectivo integral é o número real
Z Z
f (x, y) dxdy =
D
lim
n
X
n→+∞
max Ai →0 i=1
f (xi , yi ) Ai
e a função f diz-se integrável (à Riemann) na região D.
Teorema. Seja D ⊆ R2 um conjunto compacto e f : D ⊆ R2 → R uma função
contı́nua. Então, f é integrável em D.
Integrais iterados
Ao supor-se que f é contı́nua e não negativa numa região rectangular D, o integral duplo
Z Z
f (x, y) dxdy
D
representa o volume sob a superfı́cie. Este volume pode ser calculado se se fatiar a região
como mostra a seguinte figura
Em limite, o volume será o produto da área seccionada
3
pela espessura da fatia dx. A área desta fatia é dada por
Z d
C (x) =
f (x, y) dy
c
(note-se que x é constante) e o volume é dado por
Z b
Z b Z d
V =
C (x) dx =
f (x, y) dy dx.
a
a
c
Este é um exemplo de um integral iterado e que se calcula integrando primeiro a y e
depois a x.
Para o cálculo de alguns integrais duplos pode-se usar os integrais iterados e para isso
define-se dois tipos de regiões elementares.
Região do tipo 1:
Se a região de integração é da forma
D = (x, y) ∈ R2 : a 6 x 6 b ∧ ϕ1 (x) 6 y 6 ϕ2 (x)
onde a, b ∈ R e as funções ϕ1 e ϕ2 são contı́nuas em [a, b].
Na região do tipo 1, o integral duplo é dado por
Z Z
f (x, y) dxdy =
D
Z
b
a
Z
!
ϕ2 (x)
f (x, y) dy dx
ϕ1 (x)
Região do tipo 2:
Se a região de integração é da forma
D = (x, y) ∈ R2 : c 6 y 6 d ∧ ψ1 (y) 6 x 6 ψ2 (y)
onde c, d ∈ R e as funções ψ1 e ψ2 são contı́nuas em [c, d].
Na região do tipo 2, o integral duplo é dado por
Z Z
D
f (x, y) dxdy =
Z
d
c
4
Z
ψ2 (y)
!
f (x, y) dx dy
ψ1 (y)
Exemplo. Calcule o integral duplo
Z Z
(x + y) dxdy
D
onde D é a região do 1o quadrante limitada pelas curvas de equações y = x2 e y = x.
Solução 1: A função f (x, y) = x + y
é contı́nua logo é integrável em D (conjunto compacto). A região é do tipo 1.
Solução 2: A função f (x, y) = x + y
é contı́nua logo é integrável em D (conjunto compacto). A região é do tipo 2.
Logo
Logo
Z Z
=
Z
1
=
1
0
=
(x + y) dxdy =
ZD x
=
(x + y) dydx
3
.
20
x4
3 2
x − x3 −
2
2
Z
dx
=
=
5
1
(x + y) dxdy =
D
Z
√
y
(x + y) dxdy
Z 1
3 2
y
3
+ y 2 − y dy
2
2
0
3
.
20
0
x2
0
Z
Z Z
y
Propriedades do integral duplo
O integral duplo verifica as seguintes propriedades.
Teorema (Linearidade). Sejam f : D ⊆ R2 → R, g : D ⊆ R2 → R funções integráveis
em D e k ∈ R. Então,
Z Z
Z Z
Z Z
1.
[f (x, y) + g (x, y)] dxdy =
f (x, y) dxdy +
g (x, y) dxdy.
D
2.
Z Z
D
kf (x, y) dxdy = k
D
Z Z
D
f (x, y) dxdy.
D
Teorema (Aditividade). Seja f : D ⊆ R2 → R uma função integrável em D e sejam D1
e D2 dois subconjuntos de D sem pontos interiores comuns e tais que
D = D1 ∪ D2 .
Se f é integrável em D1 e em D2 , então
Z Z
Z Z
Z Z
f (x, y) dxdy +
f (x, y) dxdy =
D
f (x, y) dxdy.
D2
D1
Teorema (Positividade). Sejam f : D ⊆ R2 → R, g : D ⊆ R2 → R funções integráveis
em D.
1. Se f (x, y) > g (x, y) , para todo o (x, y) ∈ D, então
Z Z
Z Z
f (x, y) dxdy >
g (x, y) dxdy.
D
D
2. Se f (x, y) > 0 , para todo o (x, y) ∈ D, então
Z Z
f (x, y) dxdy > 0.
D
O Teorema de Fubinni diz-nos em que condições o integral duplo pode ser obtido
através dos integrais iterados.
Teorema (Teorema de Fubinni). Seja D ⊆ R2 uma região que é simultaneamente do
tipo 1 e do tipo 2. Se f : D ⊆ R2 → R uma função integrável em D, então
Z Z
Z b Z ϕ2 (x)
Z d Z ψ2 (y)
f (x, y) dxdy =
f (x, y) dydx =
f (x, y) dxdy.
D
a
ϕ1 (x)
c
ψ1 (y)
Uma região diz-se elementar se for do tipo 1 ou do tipo 2.
Teorema (Teorema da média). Seja f : D ⊆ R2 → R uma função contı́nua numa região
elementar D. Então, existe um ponto (x̄, ȳ) ∈ D tal que
Z Z
Z Z
f (x, y) dxdy = f (x̄, ȳ)
dxdy = f (x̄, ȳ) × Área de D.
D
D
Teorema (Teorema da média ponderada). Sejam f : D ⊆ R2 → R e g : D ⊆ R2 → R
funções contı́nuas numa região elementar D e seja g uma função não negativa. Então,
existe um ponto (x̄, ȳ) ∈ D tal que
Z Z
Z Z
f (x, y) g (x, y) dxdy = f (x̄, ȳ)
g (x, y) dxdy.
D
D
6
Aplicações dos integrais duplos
Cálculo de áreas de regiões do plano
Seja D a região do plano do tipo 1 definida pelas condições
a 6 x 6 b ∧ ϕ1 (x) 6 y 6 ϕ2 (x) .
A função f (x, y) = 1 para todo o (x, y) ∈ D é integrável em D e tem-se
Z Z
1 dxdy =
D
Z bZ
1 dydx
ϕ1 (x)
a
=
ϕ2 (x)
b
Z
a
[ϕ2 (x) − ϕ1 (x)] dx
= Área de D.
Este raciocı́nio é igualmente válido para regiões do tipo 2. Em resumo:
Seja f : D ⊂ R2 → R definida por f (x, y) = 1. Então, a área da região D é dada
por
Z Z
Área de D =
1 dxdy.
D
Exemplo. Seja S a região do plano limitada pelas curvas de equação y = ex , y = ln x,
x = 1 e x = e.
Então,
Área de S =
=
Z eZ
Z1 e
1
ex
1dydx
ln x
(ex − ln x) dx
= ee − e − 1.
7
Cálculo do volume de um sólido
O volume de um sólido, limitado por uma superfı́cie z = f (x, y) (onde f é uma função
contı́nua e não negativa definida num conjunto compacto D), por uma região D do plano
e uma superfı́cie cilı́ndrica de geratriz paralela ao eixo Oz e cuja directriz é a fronteira
de D, é dado por
Z Z
Volume do sólido =
f (x, y) dxdy.
D
Seja f : D ⊆ R2 → R uma função contı́nua e D um conjunto compacto. Se um
sólido é limitado superiormente pela superfı́cie
z = ϕ2 (x, y) > 0
e inferiormente pela superfı́cie
z = ϕ1 (x, y) > 0
em que (x, y) ∈ D, então o volume do sólido é dado por
Z Z
Volume do sólido =
[ϕ2 (x, y) − ϕ1 (x, y)] dxdy.
D
Exemplo. Calcule-se o volume do sólido limitado pelas superfı́cies x = 0, y = 0, x + y +
z = 2 e z = 1.
A projecção do sólido no plano z = 1 define a região D limitada pelas rectas x = 0,
y = 0 e x + y = 1. Tem-se que
Z Z
Volume do sólido =
[(2 − x − y) − 1] dxdy
D
Z 1 Z 1−x
=
(1 − x − y) dydx
0
1
=
.
6
8
0
Massa, centro de massa e momentos
Seja T uma lâmina com a forma de uma região D do plano e seja ρ : D ⊆ R2 → R
a massa especı́fica (função que associa a cada ponto a respectiva massa por unidade
de área). A massa total de T é dada por
Z Z
M=
ρ (x, y) dxdy.
D
e as coordenadas (x̄, ȳ) do centro de massa da lâmina T são dadas por
RR
Z Z
xρ (x, y) dxdy
1
D
R
R
x̄ =
xρ (x, y) dxdy
=
M
ρ (x, y) dxdy
D
D
RR
Z Z
yρ (x, y) dxdy
1
D
ȳ = R R
yρ (x, y) dxdy.
=
M
ρ (x, y) dxdy
D
D
Se a lâmina tem massa especı́fica constante, as coordenadas do centro de massa
coincidem com as coordenadas do centro geométrico (ou centróide) de T e são
dadas por
RR
RR
xdxdy
xdxdy
D
D
x̄ = R R
=
dxdy
Área de D
D
RR
RR
ydxdy
ydxdy
D
ȳ = R RD
.
=
dxdy
Área de D
D
Seja L uma linha recta e seja d : D ⊆ R2 → R a distância do ponto (x, y) ∈ D
à recta L. O momento de inércia do conjunto D relativo à recta L, que se
representa por IL , é o seguinte integral
Z Z
IL =
d2 (x, y) ρ (x, y) dxdy
D
em que g é a massa especı́fica. Em particular, os momentos de inércia em relação
aos eixos coordenados são
Z Z
IX =
y 2 ρ (x, y) dxdy
D
e
IY =
Z Z
x2 ρ (x, y) dxdy.
D
9
Mudança de variáveis em integrais duplos
O objectivo da mudança de variáveis é simplificar o cálculo do integral duplo.
Definição. Seja D ⊆ R2 um conjunto aberto. A função ϕ : D → R2 diz-se uma mudança
de variáveis, se verificar as seguintes condições:
1. ϕ é de classe C 1 ;
2. ϕ é injectiva;
3. O jacobiano de ϕ é não nulo, ou seja, |Jϕ (x, y)| =
6 0, ∀ (x, y) ∈ D.
Teorema (Teorema de mudança de variáveis). Seja D ⊆ R2 um conjunto aberto
e limitado e seja ϕ : T → R2 uma mudança de variáveis tal que T = ϕ (D) e
f : D → R uma função integrável. Então,
Z Z
Z Z
f (x, y) dxdy =
f [ϕ (u, v)] |det Jϕ (u, v)| dudv.
D
T
O cálculo do integral duplo
Z Z
D
(y − x) dxdy
7
1
onde D é a região do plano xOy limitada pelas rectas y = x+1, y = x−3, y = − x+
3
3
1
e y = − x+5
3
é dado por
Z Z
Z
(y − x) dxdy =
D
3
Z
1
+
Z
3
= −8
x+1
− 31 x+ 37
4
Z
(y − x) dydx +
− 13 x+5
− 13 x+ 73
(y − x) dydx +
10
Z
6
4
Z
− 31 x+5
x−3
(y − x) dydx
e o seu cálculo é trabalhoso. Se se fizer a mudança de variáveis
u=y−x
v = y + 13 x
as rectas y = x + 1, y = x − 3 transformam-se respectivamente em u = 1 e u = −3 e
1
7
1
7
as rectas y = − x + e y = − x + 5, nas rectas v = e v = 5. Geometricamente a
3
3
3
3
nova região de integração é
Ao resolver o sistema de equações em ordem a x e y, obtém-se
x = − 34 u + 34 v
y = 41 u + 43 v
e conclui-se que a mudança de variável ϕ é injectiva e invertı́vel. O Jacobiano da
transformação é dado por
∂x ∂x ∂v J = ∂u
∂y
∂y ∂u3 ∂v3 −
= 14 34 4
4
9
3
= − −
16 16
3
= −
4
e o integral pedido pode ser calculado da seguinte maneira:
Z Z
Z Z 3
1
3
3
3
(y − x) dxdy =
u + v − − u + v − dudv
4
4
4
4
4
D
T
Z 5Z 1
3
u dudv
=
4 73 −3
= −8.
11
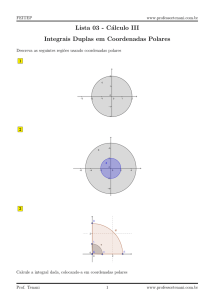
Coordenadas Polares
As coordenadas polares (r, θ) de um ponto do plano xOy são definidas por
x = r cos θ
y = r sin θ
Estas coordenadas podem ser obtidas em função da distância r do ponto P à origem
do referencial e do ângulo θ que o vector posição do ponto faz com o semieixo positivo
dos xx.
As coordenadas polares e as cartesianas verificam as seguintes relações:
(
r2
=
x2 + y 2
x = r cos θ
y
e
tan θ =
, se x 6= 0.
y = r sin θ
x
exemplo, o ponto Q de coordenadas cartesianas (1, 1) tem por coordenadas polares
√ Por
π
2,
.
4
Note-se que se escolhe r não negativo e θ ∈ [0, 2π[.
Seja D = {(r, θ) ∈ R2 : r > 0 ∧ 0 6 θ < 2π} e seja ϕ : D → R2 a função definida
por ϕ (r, θ) = (r cos θ, r sin θ) = (x, y). Então, ϕ é de classe C 1 em R2 , invertı́vel e , além
disso,
∂x ∂x ∂r
∂θ det Jϕ = ∂y
∂y ∂r ∂θ
cos θ −r sin θ = sin θ r cos θ = r.
Em D, a função ϕ é uma mudança de variáveis.
12
Exemplo. A região do plano definida por
(x, y) ∈ R2 : x2 + y 2 6 1
é definida em coordenadas polares por
{(r, θ) : 0 6 r 6 1 ∧ 0 6 θ < 2π}
Exemplo. O volume de uma esfera de raio 1 pode ser obtido por
Z Z p
1 − x2 − y 2dxdy
V =2
S
onde S é o cı́rculo definido pela equação x2 + y 2 6 1. Para calcular o integral duplo faz-se
uma mudança de variáveis para coordenadas polares
Z 2π Z 1 √
V = 2
1 − r 2 × r drdθ
0
0
4
π.
=
3
13
Integrais triplos
Uma região D ⊆ R3 diz-se decomponı́vel numa malha constituı́da por n paralelipı́pedos
Di (i = 1, . . . , n) se a união desses paralelipı́pedos é igual a D e a intersecção dos conjuntos
dos pontos interiores de Di dois a dois, é vazia. Seja Vi o volume do paralelipı́pedo Di .
Definição. Seja f : D ⊆ R3 → R uma função limitada e definida num intervalo
compacto (fechado e limitado) D ⊆ R3 . Diz-se que f é integrável à Riemann em
D se o limite
n
X
f (xi , yi , zi ) Vi
lim
n→+∞
max Vi →0 i=1
existe e não depende da decomposição de D nem da escolha dos pontos arbitrários
(xi , yi , zi ). O respectivo integral é o número real
Z Z Z
f (x, y, z) dxdydz =
D
lim
n
X
n→+∞
max Vi →0 i=1
f (xi , yi , zi ) Vi
e a função f diz-se integrável (à Riemann) na região D.
As propriedades do integral triplo são semelhantes às do integral duplo. Por exemplo,
seja D o subconjunto de R3 caracterizado pelas condições

 g1 (x, y) 6 z 6 g2 (x, y)
f1 (x) 6 y 6 f2 (x)

a 6 x 6 b,
então o integral triplo pode ser calculado por meio de sucessivos integrais
! !
Z Z Z
Z
Z
Z
b
f2 (x)
g2 (x,y)
f (x, y, z) dxdydz =
D
f (x, y, z) dz dy dx.
a
f1 (x)
g1 (x,y)
No integral triplo se a função integranda é constante e igual a 1, então o integral triplo
Z Z Z
Volume da região D =
1dxdydz
D
dá-nos o volume da região de integração.
14
Exemplo. Calcule-se o volume do sólido no 1o octante limitado pelo plano de equação
y + z = 4, pela equação y = x2 e pelos planos coordenados.
V
=
=
Z Z Z
Z
0
D
2 Z 4
128
=
.
15
x2
1dxdydz
Z 4−y
1dz dy dx
0
Mudança de variáveis em integrais triplos
O Teorema de mudanças de variáveis em integrais duplos é naturalmente generalizado a
integrais triplos. Em seguida apresentar-se-ão algumas mudanças de variáveis.
Coordenadas cilı́ndricas
Considere-se a função ϕ̄ : R+ × [0, 2π[ × R → R3 definida por

 x = r cos θ
y = r sin θ

z = z.
As coordenadas cilı́ndricas substituem x e y pelas suas coordenas polares e mantêm
a coordenada z. O Jacobiano desta transformação é
cos θ −r sin θ 0 det Jϕ̄ = sin θ r cos θ 0 = r.
0
0
1 15
Exemplo. Calcule-se o integral triplo
Z Z Z
zx
2 +y 2
dxdydz
V
em que V é o sólido limitado pelo cilindro x2 + y 2 = 4 e pelos planos z = 0 e z = 1. Ao
recorrer-se às coordenadas cilı́ndricas, tem-se que
Z Z Z
Z 2 Z 1 Z 2π
2
x2 +y 2
z
dxdydz =
z r r dθdzdr
0
V
0
0
= π ln 5.
Coordenadas esféricas
Considere-se a função ϕ̄ : R+ × [0, 2π[ × ]0, π[ → R3 definida por

 x = r cos θ sin ϕ
y = r sin θ sin ϕ

z = r cos ϕ
O Jacobiano das coordenadas esféricas é
cos θ sin ϕ −r sin θ sin ϕ r cos θ cos ϕ
det Jϕ̄ = sin θ sin ϕ r cos θ sin ϕ r sin θ cos ϕ
cos ϕ
0
−r sin ϕ
= −r 2 sin ϕ.
Exemplo. Calcule-se a massa da coroa esférica situada entre as esferas de centro na
origem e raios 1 e 2 e em que a massa especı́fica é directamente proporcional ao quadrado
da distância desse ponto à origem, ou seja
µ (x, y, z) = k x2 + y 2 + z 2 ,
com k ∈ R. A massa da coroa é dada por
Z Z Z
M=
µ (x, y, z) dxdydz
C
onde C é a coroa esférica. Como a região de integração é do tipo esférico a passagem a
coordenadas esféricas irá simplificar substancialmente o cálculo integral. Como
x2 + y 2 + z 2 = 1 ⇒ r = 1
e
x2 + y 2 + z 2 = 4 ⇒ r = 2.
Logo
M =
Z
2π
0
Z
π
0
124
πk.
=
5
Z
2
kr 2 r 2 sin ϕ drdϕdθ
1
16