Prova 3 Cálculo I
26/06/2014 – Prof. Luis
Nome:_______________________________________________RA:______________
Questão 1: Calcule a Integral
x3 + x + 1
dx (1,5 pontos)
a) ∫ 4
x + 2x2 + 4 x
b)
∫ sen
2
x cos3 x dx (1,5 pontos)
Questão 2: Calcule a Integral (1,5 pontos)
∫
2
0
x3 + x 2 − 12 x + 1
dx
x 2 + x − 12
Questão 3: Calcule a Integral (2 pontos)
∫ sen ( ln x ) dx
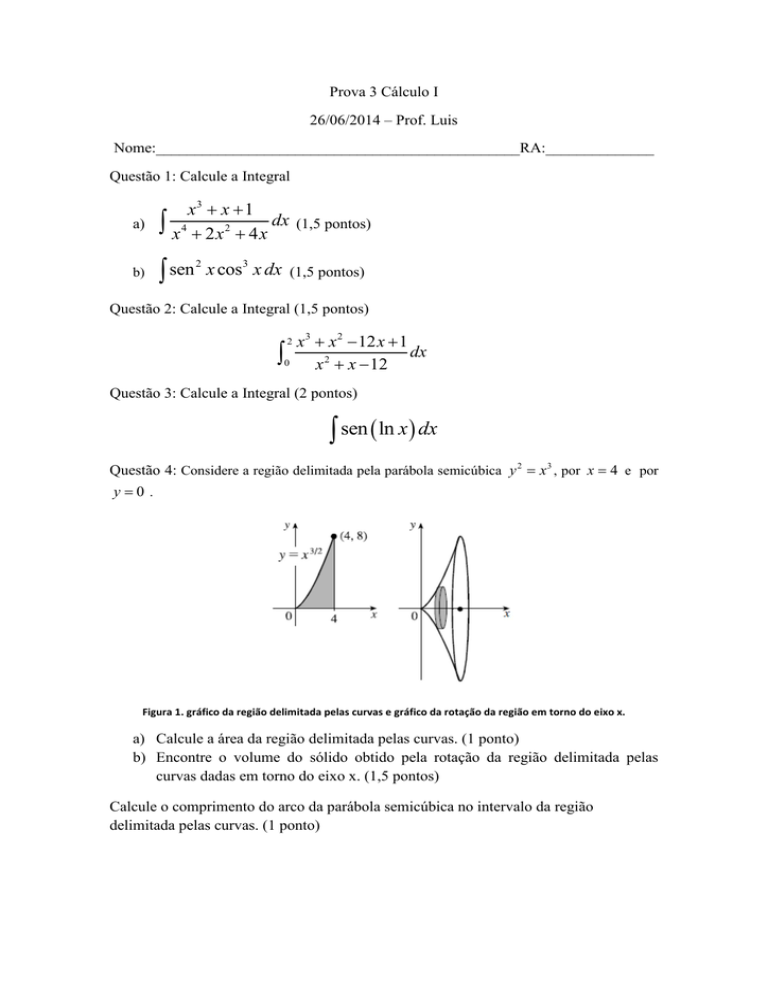
Questão 4: Considere a região delimitada pela parábola semicúbica y 2 = x 3 , por x = 4 e por
y=0 .
Figura 1. gráfico da região delimitada pelas curvas e gráfico da rotação da região em torno do eixo x.
a) Calcule a área da região delimitada pelas curvas. (1 ponto)
b) Encontre o volume do sólido obtido pela rotação da região delimitada pelas
curvas dadas em torno do eixo x. (1,5 pontos)
Calcule o comprimento do arco da parábola semicúbica no intervalo da região
delimitada pelas curvas. (1 ponto)
Gabarito.
Questão 1
u = x4 + 2 x2 + 4 x
du = 4 ( x3 + x + 1) dx
a)
b)
2)
3.
1
x3 + x + 1
1 1
1
∴ ( x + x + 1) dx = du → ∫ 4
dx = ∫ du = ln u + C
2
4
x + 2x + 4x
4 u
4
Assim,
3
integrando por partes duas vezes:
Questão 4
a)
A=∫
4
L=∫
4
0
4
2
64
x dx = x 5/2 =
5
5
0
3/2
b)
c)
0
1 + ( y ' ) dx
2
y = x 3/ 2 ⇒ y ' =
3 1/ 2
9
2
x ∴ ( y ') = x
2
4
9
x dx
0
4
9
9
4
Fazendo u = 1 + x, du = dx ⇒ dx = du
4
4
9
Os limites de integração de u ficam 0 para x = 0 e 10 para x = 4
⇒L=∫
4
1+
10
4 10
8
80 10
⇒ L = ∫ u du = u 3/ 2 =
0
9
27
27
0












