Document

TAC II – Lista 10
Prof Dra Maria Aparecida Bená
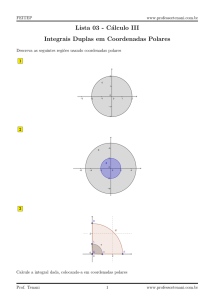
a
1.
 f x, y  dx dy , onde:
Calcular
R
a) f x, y   xe
xy
b) f x, y   x cos xy
c) f x, y   y ln x
2.
1 x  3
0  y 1
R é o retângulo
0 x2

0y
2
R é o retângulo
a)
1
 
x dy dx
1
ln x
c)
 
2 x3
1 y  2
(R:
4

)
3


 R : 3 ln 3  2 ln 2  1
2


1 y 2
1
b)
 
0
x dx dy
d)
1 x 2
(R: 0 )
1
)
3
x
 
1
(R:
0
2
x dy dx
1
y ln x dy dx
(R:
0
4 ln 2 7
 )
3
18
x 1
2
e)
e2 3
 )
(R:
4 4
4 x2
1
 
x 2 dy dx
1
0
(R:
27
)
4
Inverter a ordem de integração:

R :

0

y
4
a)
2
 
0
b)
ex
 
1
2
f  x, y  dx dy
0
2
4.
(R: e3  e  2 )
Esboçar a região de integração e calcular as seguintes integrais iteradas:
e
3.
R é o retângulo
f x, y  dy dx
0
4

2x

f  x, y  dy dx 

e
2
e
2


R :





f
x
,
y
dx
dy

f
x
,
y
dx
dy
 e  ln y
  0 1



2
Calcular:
a)
 2 x  y  dx dy
R
b)

R
x2
dx dy
2
y
R: x  y 2  1 ; x  5 ;
y  1 ; y  2 .
R: região delimitada por
1
y  x ; y  ; x  2.
x
1/4
(R:
1533
)
20
(R:
9
)
4
TAC II – Lista 10
Prof Dra Maria Aparecida Bená
a
c)
 x  y  dx dy
R: região delimitada por
y  x 2  1 ; y  1  x 2 ;
R
(R: 0 )
x  1 ; x  1.
d)

e  x dxdy
R: região delimitada por
x  4y ; y  0; x  4.
2
R
e)
(R:
1
1  e 16  )

8 
R: triângulo de vértices 1,1 ,
1,2 e 2,1 .
 1  x  y  dx dy
R
5.
Calcular a área da região R delimitada por x  y 2  1 e x  y  3 .
6.
Escreva em coordenadas polares:
(R:
(R:
3
)
2
9
u.a )
2
a) Circunferência de centro a,0 e raio a, a  0 .
(R: r  2 a cos θ )
b) A equação x  y 
(R: r  1 cos  )
2
2
x2  y2  x
7.
Calcular o volume do sólido acima do plano xy delimitado por
z  4  2 x 2  2 y 2 . (Use coordenadas polares).
8.
Calcular o volume do sólido abaixo do plano xy delimitado por
z  x 2  y 2  9 . (Use coordenadas polares).
9.
Usando coordenadas polares, calcule:
a)

a 2  x 2  y 2 dy dx
R
d)
2
2
  x  y 
R
81
 u.v )
2
(R: 0 )

- 1  x  1
R :
2

0  y  1 - x
 y dy dx
R
c)
(R:

 2  x  2
R :
2
2

 4  x  y  4  x
 y dy dx
R
b)
(R: 4 u.v )

0  x  a
R :
2
2

0  y  a  x
(R:
(R:
 a3
6
2
dx dy
R : 2  x2  y2  4
2/4
2
)
3
(R:
)

)
4
TAC II – Lista 10
Prof Dra Maria Aparecida Bená
a
e)
2 x 2  y 2 dx dy
e

R
f)
 x dx dy
R : x 2  y 2  4x  0
R
g)
  x
R
i)
R : x2  y2  4
(R:
 8 
 e 1 )
2

(R: 8 )
2  y 2  dx dy , onde R é dada por:


Círculo centrado na origem de raio a.
ii) Círculo centrado em a,0 de raio a.
iii) Círculo centrado em 0, a  de raio a.
 a 4 3a 4 3a 4 
R :

;
;

2
2
2 


R: região do 1º
quadrante delimitada
x2  y2  1 ,
por
h)
x2  y2  4 , y  x
e y  0.
 x dy dx
R
i)
 xy dx dy
x2 y2
R:

1
4
9
R
j)
2
2
 x  1   y  2 dx dy
R
k)
 8  x  y  dx dy
R
l)
R : x  12 
 y  22  1
R : x2  y2  1
dxdy

3
R
2
2
1  x  y  2



R : x2  y2  a2
(1º quadrante)
1

7 2
R :


6 

R : 0
 2 
R :

3 

R : 8 



1 
 

R
:
1


2

1  a 2  


dA onde R é a região do semiplano x  0 , interna à cardioide
2
2
R x y
(figura com formato de coração) r  1 cos  e externa à circunferência de centro na
origem e raio 1. (Figura abaixo).
10. Calcule
3/4
TAC II – Lista 10
Prof Dra Maria Aparecida Bená
a
R : 2
4/4