Gráfico das Funções Trigonométricas: Uma aplicação

Objetos de Aprendizagem
Funções Trigonométricas
————————————————————————————————————————
Gráfico das Funções Trigonométricas: Uma aplicação
————————————————————————————————————————
Objetivos.
Exemplificar a periodicidade das funcões seno e cosseno através de uma situação problema envolvendo o movimento de marés.
Descrição Geral.
Apresenta dados tabelados de uma situação real, obtidos da tábua de marés do Porto de Cabedelo-PB
no dia 01/04/2015 (<www.pbagora.com.br/tabuadasmares.php>) e usa a função f (t) = a+b cos(ct +
d) como um modelo simplificado, consideramos valores aproximados pela média, tendo como base as
dados observados em um único dia, para representar a evolução das marés em um período de 48 horas.
(Um modelo completo para a previsão de marés, usando a função cosseno, pode ser encontrado em
<http://www.tabuademares.com/mares>.).
Esta atividade foi elaborada para ser aplicada na sala de aula (ou laboratório de informática) sob a
orientação do professor, com a duração de uma aula de 50 minutos.
Sugestões de procedimentos ou questionamentos.
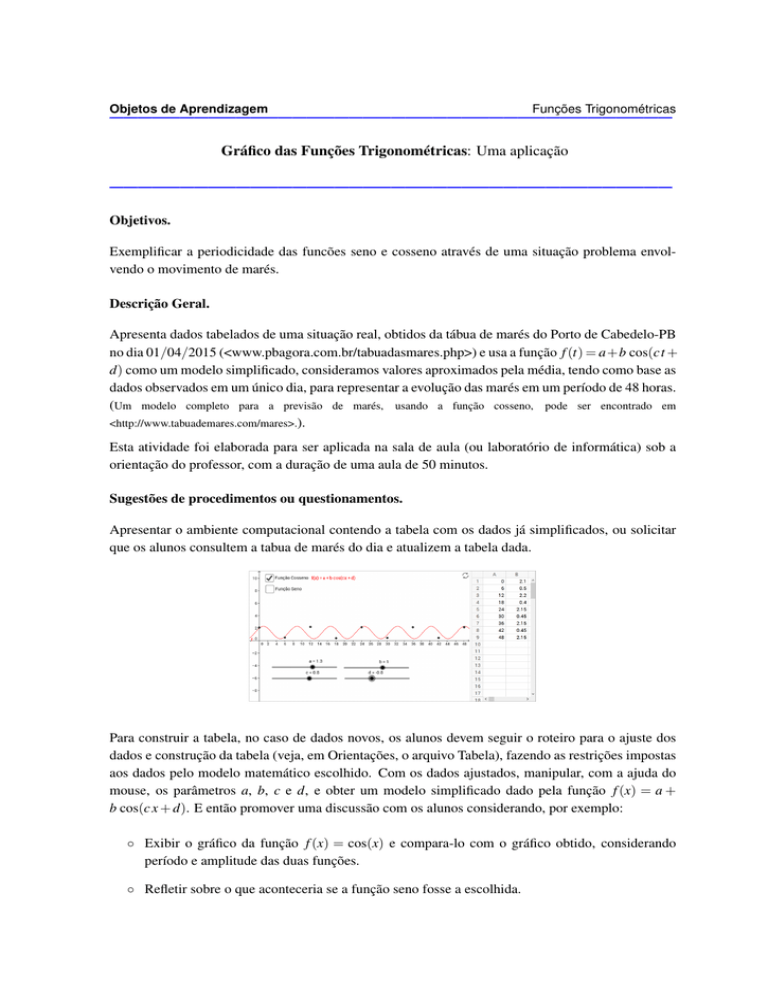
Apresentar o ambiente computacional contendo a tabela com os dados já simplificados, ou solicitar
que os alunos consultem a tabua de marés do dia e atualizem a tabela dada.
Para construir a tabela, no caso de dados novos, os alunos devem seguir o roteiro para o ajuste dos
dados e construção da tabela (veja, em Orientações, o arquivo Tabela), fazendo as restrições impostas
aos dados pelo modelo matemático escolhido. Com os dados ajustados, manipular, com a ajuda do
mouse, os parâmetros a, b, c e d, e obter um modelo simplificado dado pela função f (x) = a +
b cos(c x + d). E então promover uma discussão com os alunos considerando, por exemplo:
◦ Exibir o gráfico da função f (x) = cos(x) e compara-lo com o gráfico obtido, considerando
período e amplitude das duas funções.
◦ Refletir sobre o que aconteceria se a função seno fosse a escolhida.
◦ Promover uma discussão sobre aproximação de dados reais por uma curva. Modelos matemáticos de fenômenos naturais e as simplificações e/ou restrições necessárias, etc.
◦ Para encerrar essa atividade o professor pode convidar a turma a obter o modelo simplificado,
calculando os valores dos parâmetros algebricamente, como segue:
Assumindo que f (x) = a + b cos(c x + d) descreve o movimento das marés, o parâmetro c é
responsável pelo período P da função, logo
P=
2π
.
c
Observemos que quando c = 1, temos P = 2 π.
Como duas mares altas (ou baixas) consecutivas ocorrem em um intervalo de tempo médio de
12 horas, temos que o período da função que modela o movimento das marés é 12. (P = 12).
Assim,
π
2π
⇒c= .
12 =
c
6
Um valor máximo da função ocorre quando t = 0, então, o parâmetro d, responsável pelo
deslocamento horizontal do gráfico da função, deve ser nulo, ou seja, d = 0.0
Os valores de a e b podem ser obtidos fazendo t = 0 e t = 6, respectivamente, na função
f (t) = a + b cos( π6 t).
f (0) = a + b cos(0) = 2, 15 ⇒ a + b = 2, 15;
f (6) = a + b cos(π) = 0, 45 ⇒ a − b = 0, 45.
Resolvendo o sistema formado pelas equações acima, temos a = 1, 30 e b = 1, 05. Logo,
π t
f (t) = 1, 30 + 1, 05 cos
6
é o modelo matemático procurado.
2