ANÁLISE DAS TENSÕES

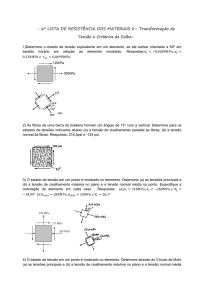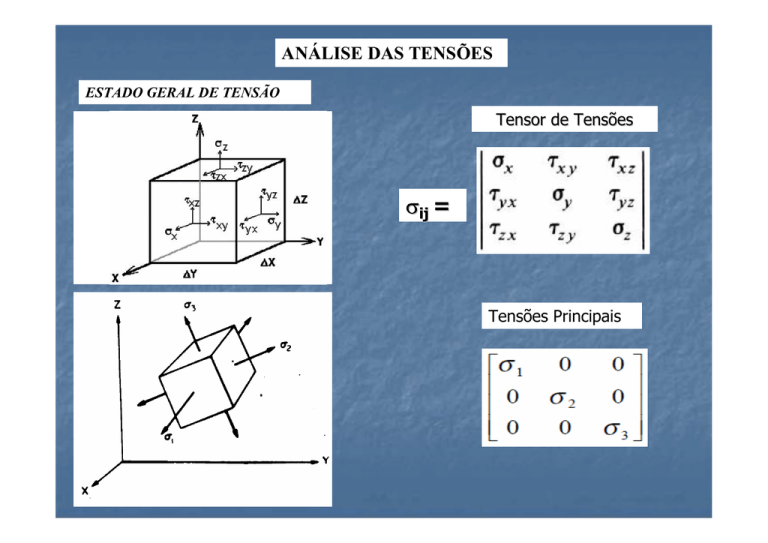
ANÁLISE DAS TENSÕES
ESTADO GERAL DE TENSÃO
Tensor de Tensões
σij =
Tensões Principais
Tensões Principais
σ 1, 2 =
Estado plano de tensão
σ x +σ y
2
±
(σ
−σ y )
2
x
+ τ xy
2
2
σ 3 − I1σ 2 + I 2σ − I 3 = 0
Solução
I1, I2, I3
Estado de tensão 3D
σ1 ≥ σ2 ≥σ3
3 raízes
Invariantes das tensões
I1 = σ x + σ y + σ z
I 2 = σ xσ y + σ yσ z + σ zσ x − τ xy − τ yz − τ zx
2
2
2
I 3 = σ xσ yσ z + 2τ xyτ yzτ zx − σ xτ yz − σ yτ zx − σ zτ xy
2
2
2
Direções Principais
(σ x - σ p )
τ xy

(σ y - σ p )
 τ yx
τ
τ zy
 zx
τ xz
 l 
 
τ yz
 m  = 0
(σ z - σ p ) n 
Desenvolvendo a equação para σ1 Obtém-se l1, m1 e n1
Lembrando que
Para σ2 obtém-se l2, m2 e n2
Para σ3 obtém-se l3, m3 e n3
l1 + m1 + n1 = 1
2
2
2
Análise de Tensão 3D
Tensão normal e de cisalhamento num plano qualquer
Resultante no plano ABC
S 2 = σ N +τ 2
2
ou
S 2 = Sx + S y + Sz
2
2
2
Cossenos diretores
l = cos α
m = cos β
n = cos γ
Para calcular Sx, Sy e Sz
S x 
l 
 
m
S
=
σ
.
y
ij
 
 
S 
n 
 z
[ ]
σ N = S xl + S y m + S z n
Círculo de Mohr 3D
Máximas tensões de cisalhamento no sistema 3D
CIRCULO DE MOHR PARA O ESTADO TRIPLO DAS TENSÕES
Determinação da tensão normal e de cisalhamento num plano qualquer
Critérios de Escoamentos que
estudaremos:
Materiais Dúcteis:
Teoria da Tensão de Cisalhamento Máxima ou Critério
de Escoamento de Tresca
Teoria da Energia de Distorção Máxima ou Critério de
von Mises.
Materiais Frágeis:
Teoria da Tensão Normal Máxima –W. Rankine
Teoria da Tensão de Cisalhamento Máxima ou
Critério de Escoamento de Tresca
τ max ≥ K
abs
K= tensão de escoamento no cisalhamento
σ max − σ min
2
=K
σ max − σ min = 2 K
Qual o valor de K?
No teste de tração: σmax= σ1; σmin=0
No escoamento: σ1= σe=2K
σ e − 0 = 2K
σ
K = e ⇒ σ max − σ min = σ e
2
Fazendo σ2=0:
caso1 : σ 1 ⟩ 0⟩σ 3
⇒ σ1 − σ 3 = σ e
caso2 : σ 3 ⟩ 0⟩σ 1
⇒ σ 3 − σ1 = σ e
caso3 : σ 1 ⟩σ 3 ⟩ 0
⇒ σ1 − 0 = σ e
caso4 : σ 3 ⟩σ 1 ⟩ 0
⇒ σ3 − 0 = σe
caso5 : 0⟩σ 1 ⟩σ 3 ⟩
⇒ 0 −σ3 = σe
caso6 : 0⟩σ 3 ⟩σ 1
⇒ 0 − σ1 = σ e
Teoria da Energia de Distorção Máxima ou Critério de von Mises
Quando a energia de distorção no ponto crítico do componente atingir o mesmo valor da energia
de distorção do corpo de prova no momento do seu escoamento, iniciará também o escoamento
do componente naquele ponto”
U =
1
1
1
σ 1ε 1 + σ 2 ε 2 + σ 3 ε 3
2
2
2
1
ε 1 = [σ 1 −ν (σ 2 + σ 3 )]
E
1
ε 2 = [σ 2 −ν (σ 1 + σ 3 )]
E
1
ε 3 = [σ 3 −ν (σ 1 + σ 2 )]
E
[
]
1
U=
σ 1 2 + σ 2 2 + σ 3 2 − 2ν (σ 1σ 2 + σ 1σ 3 + σ 3σ 2 )
2E
Densidade de deformação (U) é a soma de duas componentes: Hidrostática e Distorção
Hidrostática: responsável somente por mudança de volume. É associada a tensão
principal média:σmed= (σ1+σ2+σ3)/3
Distorção: responsável pela energia necessária para distorcer o elemento. Subtraindo a
parte hidrostática do estado de tensão, a parte restante da tensão, (σ1-σmed), (σ2σmed) e (σ3-σmed), provoca a energia de distorção como mostra a fig. C.
=
+
Substituindo-se σ1, σ2 e σ3 por σ1-σmed), (σ2-σmed) e (σ3-σmed), na equação de U obtém-se Ud:
Ud =
[
1 +ν
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2
6E
]
No ensaio de tração uniaxial, σ1=σe, σ2 = σ3 = 0 e temos:
(U d )e
=
1 +ν 2
σe
3E
Como a teoria de distorção máxima requer que Ud = (Ud)e temos que:
σe =
[
1
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2
2
No Caso do estado plano de tensões, σ3 = 0
]
1
2
σ 12 − σ 1σ 2 + σ 2 2 = σ e 2
σ 2 -σ 3
σ1 -σ 3
Teoria da tensão normal máxima – W. Rankine - 1800
Teoria válida para materiais frágeis
A teoria da tensão normal máxima estabelece que um material frágil falha
quando a tensão principal máxima atinge um valor limite igual ao limite de
resistência que o material suporta quando submetido à tração simples.
Caso o material esteja submetido ao estado plano de tensões tem-se que:
σ1 = σ r
σ2 =σr
Planos Octaedrais
τ oct
[
1
2
2
2
= (σ 1 − σ 2 ) + (σ 2 − σ 3 ) + (σ 3 − σ 1 )
3
σ oct =
σ1 + σ 2 + σ 3
3
]
1
2
Interpretação Física do critério de escoamento de von Mises utilizando
o valor crítico da tensão de cisalhamento octedral
τ oct
[
1
2
2
2
= (σ 1 − σ 2 ) + (σ 2 − σ 3 ) + (σ 3 − σ 1 )
3
Em tração uniaxial
τ oct =
]
1
2
2
σe
3
Igualando as equações acima:
σe
2
[
1
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ 1 )2
=
2
]
1
2
Comparação dos três critérios
Exemplos
Exemplo 1– O estado de tensão em torno de um ponto é dado
pelo tensor das tensões mostrado abaixo. Determine as tensões
principais.
- 5

σ ij =  0
 0
0
-6
- 12
0 

- 12 MPa
1 
Exemplos
Exemplo 2– O eixo maciço da figura abaixo tem raio 0,5 in e é
feito de aço com limite de escoamento σe = 36 ksi. Determinar se o
carregamento provocará falha sua falha de acordo com os critérios
de Tresca e de Von Mises.
Exemplos
Exemplo 3 - Um vaso de pressão cilíndrico usado em motor de
foguete, de parede fina, é construído de material cujo escoamento é
σe = 200 MPa, raio do cilindro = 1,25 m, pressão interna p = 0,7 MPa.
Usando um fator de segurança igual a 2, determine a espessura do
vaso, para que não ocorra falha (explosão). Obtenha a solução através
dos critérios de escoamento de Tresca e de von Mises.
Verifique, pelos critérios de Tresca e de von Mises, se o estado de
tensões representado na figura abaixo é estável. Considere σe = 200
MPa.
Exemplo 3 - Um vaso de pressão cilíndrico usado em motor de
foguete, de parede fina, é construído de material cujo escoamento é
σe = 200 MPa, raio do cilindro = 1,25 m, pressão interna p = 0,7 MPa.
Usando um fator de segurança igual a 2, determine a espessura do
vaso, para que não ocorra falha (explosão). Obtenha a solução através
dos critérios de escoamento de Tresca e de von Mises.
Exemplo 4 - Prove que a diferença máxima entre os critérios de
escoamento de Tresca e de von Mises é da ordem de 15,4%.
Exemplo 5 - Mostre que a superposição de um estado hidrostático de
tensões a um estado de tensões não altera as previsões dos critérios
de escoamento de Tresca e de von Mises.