LOM3090 - Parte 4.

Universidade de São Paulo
Escola de Engenharia de Lorena
Departamento de Engenharia de Materiais
Mecânica dos Sólidos Aplicada (LOM3090)
Prof. Dr. João Paulo Pascon
4. Critérios de Falha
• 4.1. Equações de Transformação no caso Triaxial
• 4.2. Tensões Principais e Invariantes
• 4.3. Tensões Octaédricas
• 4.4. Critérios de Fratura para Materiais Frágeis
• 4.5. Critério de Tresca
• 4.6. Critério de Von Mises
• 4.7. Componentes Hidrostático e Desviador
4. Critérios de Falha
• Critérios simples
• EPT
• Tensão no caso geral
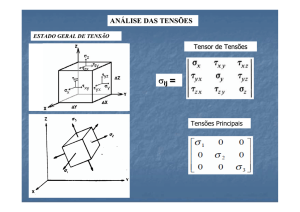
4.1. Equações de Transformação no caso Triaxial
• Estado Plano de Tensão (EPT)
• Definição das componentes e rotação do plano xy
• Relações geométricas e equilíbrio de forças
• Equações de transformação
4.1. Equações de Transformação no caso Triaxial
• Estado de Tensão 3D (Geral)
• Definição das componentes
• Rotação no espaço (plano oblíquo)
• Relações geométricas
4.1. Equações de Transformação no caso Triaxial
• Equilíbrio de forças
• Equações de transformação
• Componentes
Exemplo 4.1. Estado de Tensão 3D
• O estado de tensão num ponto é definido pelas seguintes componentes:
• σx = 200; σy = 400; σz = -100; τxy = -100; τxz = 300; τyz = 0.
• Para um plano cujo vetor normal é n = {2,2,1}, determinar as seguintes tensões:
• componentes de tensão em relação aos eixos x, y e z
• tensão normal no plano
• tensão total no plano
• tensão cisalhante no plano
x  x  xy y  xz  z 
 t nx 


 
t n   t ny   σ   n  xy x   y y   yz  z 
 


t








 nz 
z z
 xz x yz y
tn  σ  τ
t N  n n  n s
4.1. Equações de Transformação no caso Triaxial
• Estado Rotacionado
x  x  xy y  xz  z 
 t nx 


 
t n   t ny   σ   n  xy x   y y   yz  z 
 










 t nz 
xz
x
yz
y
z
z


4.1. Equações de Transformação no caso Triaxial






x '  t x '  nx '  x  x  xy y  xzz  x  xy x  y y  yzz  y  xz x  yz y  z z  z












x ' y'  t x '  ny'  x x  xy y  xzz x  xy x  y y  yzz  y  xz x  yz y  z z z


x 'z'  t x '  nz'  x  x  xy y  xzz x  xy x  y y  yz z y  xz x   yz y  z z z




y'x '  t y'  nx '  x x  xy y  xzz  x  xy x  y y  yzz  y  xz x   yz y  z z  z



 

y'z'  t y'  nz'   x x  xy y  xzz  x   xy x  y y  yzz  y   xz x   yz y  zz z
y'  t y'  n y'  x x  xy y  xzz x  xy x  y y  yzz  y  xz x   yz y  zz z

 
 

z' y'  t z'  ny'   xx  xyy  xzz  x   xyx  yy  yzz   y   xzx  yzy  zz  z
z'x '  t z'  nx '  xx  xyy  xzz  x  xyx  yy  yzz  y  xzx  yzy  zz  z






z'  t z'  nz'  xx  xyy  xzz x  xyx  yy  yzz y  xzx   yzy  zz z
Exemplo 4.2. Estado de Tensão 3D
• O estado de tensão num ponto é definido pelas seguintes componentes:
• σx = 1000; σy = -600; σz = 400; τxy = 800; τxz = τyz = 0.
• O sistema de coordenadas (x,y,z) é modificado para (x’,y’,z’), sendo que o eixo z’ coincide com o
eixo z, e o plano xy é rotacionado no sentido anti-horário em 30º. Para o novo sistema, determinar
as componentes de tensão.
4.2. Tensões Principais e Invariantes
t1  1nX
• Estado Plano de Tensão (EPT)
• Tensões principais
t 2   2n Y
t3  3nZ
• Direções (ou planos) principais
• Estado de tensão 3D
• Invariantes de tensão
• Método de Cardano
• Direções principais
x  x  xy  y  xz  z    

  1 x
t1   xy  x   y  y   yz  z   1 y 

 











xz
x
yz
y
z
z

1
z



Exemplo 4.3. Estado de Tensão 3D
• O estado de tensão num ponto é definido pelas seguintes componentes:
• σx = 100; σy = 200; σz = -100; τxy = -200; τxz = -300; τyz = 100.
• Determinar:
• invariantes de tensão
• invariantes modificados de tensão
• tensões principais
• direções principais (*)
I1   x   y   z
I 2   x y   x z   y z   xy 2   xz 2   yz 2
I 3   x y z   x yz 2   y xz 2   z xy 2  2 xy xz yz
* Máxima tensão cisalhante
• Máximo cisalhamento e direções correspondentes a partir das direções principais
1 0 0   x   1 x 

  
1    2   1 2    2
t   0 2 0  0 y   2y   t  
2  3 z 
R 2   1 xx  2 y

x
x
        
   1 

 0  0  
1



3




0

z

3
z


 y   

 y 

 y 

2
2
  

  

   1 




 z
 z
n  t  n 11 x  x  2 yz  y   3z2z  1 x 2  2 y 20 3z 2
2 



  R 2  n 2 
 max 12  


 1  2 2  x 2 y2  1  3 2  x 2z 2  2  3 2  y2z 2
1  2
2
 max 13  
1  3
2
 max 23  
 2  3
2
4.3. Tensões Octaédricas
• Teoria da plasticidade (critério de plastificação)
• Planos octaédricos
• Tensões octaédricas
Exemplo 4.4. Tensões Octaédricas
• Para o estado de tensão do Exemplo 4.3, determinar as tensões octaédricas (normal e cisalhante).
 100 200 300 
σ   200 200 100 
 300 100 100 
4.4. Critérios de Fratura para Materiais Frágeis
• Material dúctil x material frágil
• Fratura frágil
• Concreto
• Cerâmica
• Vidro
4.4. Critérios de Fratura para Materiais Frágeis
• Materiais sob Estado Plano de Tensão (EPT)
• Tensões principais
• Critério da máxima tensão normal (Coulomb)
• Critério de Rankine
4.4. Critérios de Fratura para Materiais Frágeis
• Materiais sob Estado Plano de Tensão (EPT)
• Critério do círculo de Mohr
• Tensões principais com mesmo sinal
• Tensões principais com sinal diferente
• Diagrama simplificado
Exemplo 4.5. Critério de Fratura para Material Frágil
• Para os dois estados planos de tensão, determinar se ocorrerá ruptura:
• (a) critério de Coulomb (σU = 120 MPa);
• (b) critério de Rankine (σUT = 80 MPa, σUC = 200 MPa);
• (c) critério de Mohr (σUT = 80 MPa, σUC = 200 MPa).
4.5. Critério de Tresca
• Critério de plastificação para material dúctil
• Observação experimental (estado uniaxial)
• Modelo de Tresca (EPT):
• Tensões principais com mesmo sinal
• Tensões principais com sinais opostos
4.6. Critério de Von Mises
• Critério de plastificação para material dúctil
• Energia de deformação específica (densidade de energia de deformação)
• Definição de trabalho (ou energia)
• Estado uniaxial
• Estado 3D
• Observação experimental
• Modelo de von Mises
• Teoria da máxima energia de distorção
4.6. Critério de Von Mises
ud 
1 
2
2
2
1   m    2   m    3   m   2  1   m  2   m   2  1   m  3   m   2  2   m  3   m  


2E 
ud 
1 1
2
2
2
21   2   3    2 2   1   3    2 3   1   2   2  2 1   2   3  2 2   1   3 

2E 9 
2  21   2   3  2 3   1   2   2  2 2   1   3  2 3   1   2  
ud 

 

1 1
412   2 2   32  41 2  41 3  2 2 3  4 2 2   12   32  41 2  4 2 3  2 1 3 

2E 9
 4
2
3


 12   22  41 3  4 2 3  21 2  2 41 2  212  21 3  2 2 2  1 2   2 3  2 2 3  1 3   32




2 41 3  212  21 2  2 2 3  1 2   2 2  2 32  1 3   2 3

2 4 2 3  21 2  2 22  21 3  12  1 2  2 32  1 3   2 3 

ud 
1 
1  
6  6  12   2 2   32   6  6 1 2  1 3   2 3   
2  12   2 2   32  2  1 2   1 3   2 3  





18E
6E
ud 
1   2
1  21 2   2 2  12  21 3   32   2 2  2 2 3   32 


6E



 

 


4.6. Critério de Von Mises
• Modelo de von Mises
• Estado 3D
• Estado uniaxial
• EPT
Exemplo 4.6. Critério de Plastificação para Material Dúctil
• Para os dois estados planos de tensão abaixo, determinar se ocorrerá plastificação:
• (a) critério de Tresca (σe = 120 MPa);
• (b) critério de von Mises (σe = 100 MPa).
Exemplo 4.7. Critérios para Estados Triaxiais
• Para o estado de tensão triaxial referente ao Exemplo 4.3, verificar os critérios de
Coulomb, Tresca e von Mises para os seguintes materiais:
• Concreto de alto desempenho (σU = 100 MPa);
• Cerâmicas reforçadas por cristais de alumina (σU = 180 MPa);
• Aço estrutural A36 (σe = 250 MPa);
• Liga de alumínio 2014-T6 (σe = 300 MPa);
• Liga de titânio (σe = 924 MPa).
1  486 , 952MPa
 2  319 ,127MPa
 3  32 ,175MPa
Exemplo 4.8. Critério para EPT
• Para uma viga em balanço com 2 m de comprimento, seção transversal retangular (1 cm
de largura e 50 cm de altura), e com uma carga transversal de 10 kN na extremidade livre,
determinar se ocorrerá falha ou escoamento para os seguintes materiais:
• Coulomb: σrup = 30 MPa
• Mohr: σrup (tração) = 10 MPa; σrup (compressão) = 50 MPa
• Tresca: σesc = 80 MPa
• Von Mises: σesc = 150 MPa
4.7. Componentes Hidrostático e Desviador
• Mudança de volume em regime plástico
• Deformação volumétrica
• Tensão hidrostática
• Módulo de compressibilidade volumétrica
• Limite para o coeficiente de Poisson
• Tensão desviadora
Exemplo 4.9. Tensões hidrostática e desviadora
• Para o estado de tensão do exemplo 4.3, determinar:
• (a) as parcelas hidrostática e desviadora;
• (b) os invariantes da parcela desviadora
I1   x   y   z
I 2   x y   x z   y z   xy 2   xz 2   yz 2
I 3   x y z   x yz 2   y xz 2   z xy 2  2 xy xz yz