Apresentação do PowerPoint
Propaganda
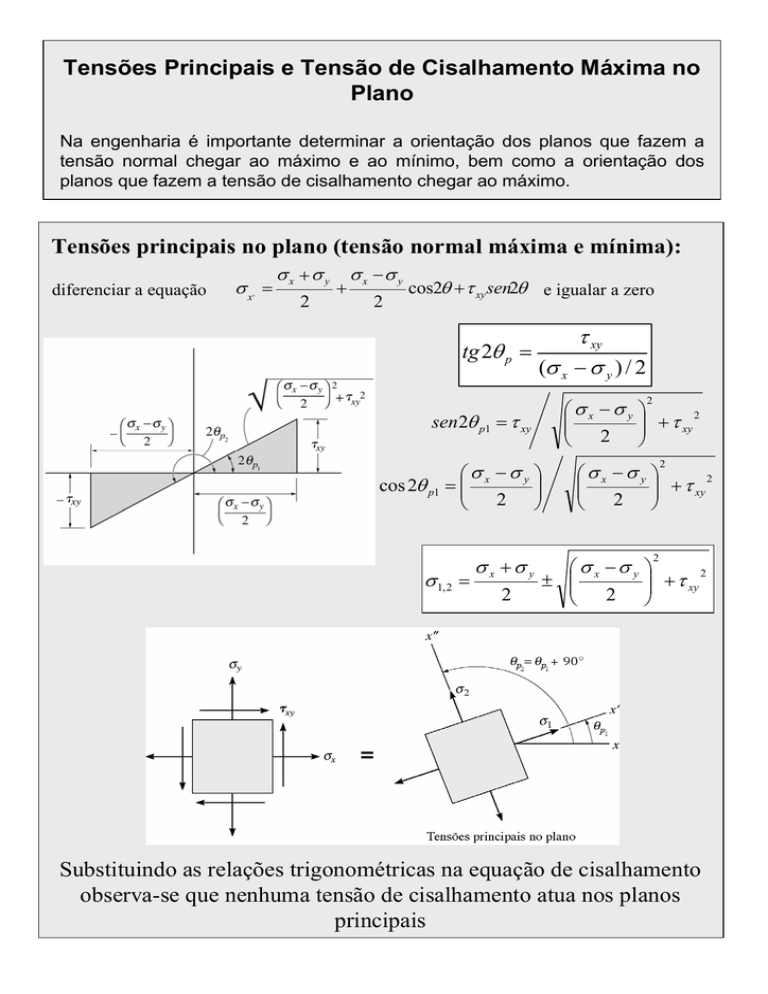
Tensões Principais e Tensão de Cisalhamento Máxima no Plano Na engenharia é importante determinar a orientação dos planos que fazem a tensão normal chegar ao máximo e ao mínimo, bem como a orientação dos planos que fazem a tensão de cisalhamento chegar ao máximo. Tensões principais no plano (tensão normal máxima e mínima): diferenciar a equação σx = , σ x +σ y σ x −σ y 2 + 2 cos2θ + τ xy sen2θ e igualar a zero tg 2θ p = τ xy (σ x − σ y ) / 2 ⎛σx −σ y ⎞ 2 ⎜⎜ ⎟⎟ + τ xy ⎝ 2 ⎠ 2 sen2θ p1 = τ xy ⎛σ −σ y ⎞ ⎟⎟ cos 2θ p1 = ⎜⎜ x ⎝ 2 ⎠ σ 1, 2 = σ x +σ y 2 ⎛σx −σ y ⎞ 2 ⎜⎜ ⎟⎟ + τ xy ⎝ 2 ⎠ ⎛ σ x −σ y ± ⎜⎜ ⎝ 2 2 2 ⎞ ⎟⎟ + τ xy 2 ⎠ Substituindo as relações trigonométricas na equação de cisalhamento observa-se que nenhuma tensão de cisalhamento atua nos planos principais Tensão de cisalhamento máxima: diferenciar a eq. τ , ,, xy =− σ x −σ y 2 sen2θ +τ xy cos2θ e igualar a zero tg 2θ c = − (σ x − σ y )/ 2 τ xy ⎛σ −σ y ⎞ 2 ⎟⎟ + τ xy = ⎜⎜ x ⎝ 2 ⎠ 2 τ máx Planos para a tensão de cisalhamento máxima são determinados orientando-se um elemento a 45º da posição do elemento que define os planos da tensão principal Substituindo as relações trigonométricas na equação da tensão normal tem-se a tensão média τ méd = σx +σy 2 27) O estado plano de tensões em determinado ponto de um corpo é mostrado no elemento. Representar esse estado de tensão em termos das tensões principais. 28) O estado plano de tensões em determinado ponto de um corpo é mostrado no elemento acima. Representar esse estado de tensão em termos da tensão de cisalhamento máxima no plano e da tensão normal média a ela associada.
