Estado duplo ou, Estado plano de tensões. A tensão que atua em

Estado duplo ou, Estado plano de tensões.
A tensão que atua em um ponto é função do plano pelo qual se faz o estudo.
Seja um ponto, com dimensões infinitesimais, que pertence a um corpo em
equilíbrio, onde em um de seus planos (plano 0), atua uma tensão normal ( 0)
e uma tensão de cisalhamento ( o). Suponha-se, também, que no plano
asterisco (*), também atuem uma tensão normal ( *) e uma tensão de
cisalhamento ( *).
Figura V-5- Tensão normal e de cisalhamento que atuam no plano 0 e no plano *.
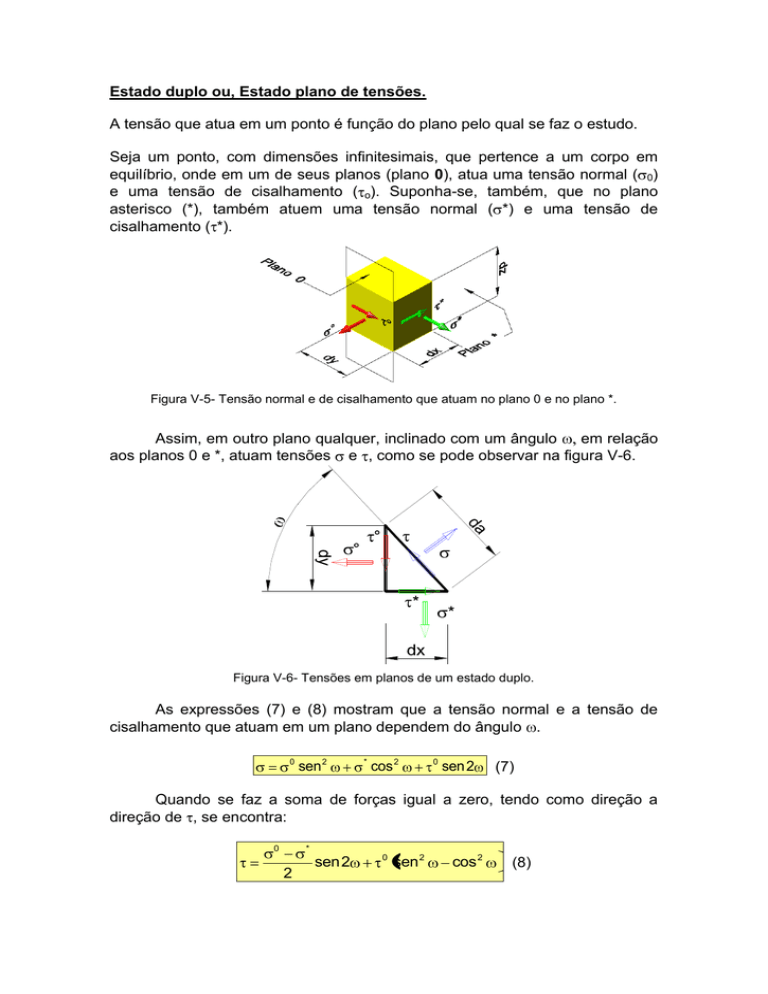
Assim, em outro plano qualquer, inclinado com um ângulo
em relação
aos planos 0 e *, atuam tensões e , como se pode observar na figura V-6.
da
Figura V-6- Tensões em planos de um estado duplo.
As expressões (7) e (8) mostram que a tensão normal e a tensão de
cisalhamento que atuam em um plano dependem do ângulo .
0
sen 2
*
cos 2
0
sen 2
(7)
Quando se faz a soma de forças igual a zero, tendo como direção a
direção de , se encontra:
0
*
2
sen 2
0
sen 2
cos 2
(8)
Existirá um máximo e um mínimo para a tensão normal. A estas tensões
se dá o nome de Tensões Principais e se indica por 1 e 2, respectivamente.
Aos planos onde atuam as tensões principais se dá o nome de planos
principais e são indicados por 1 e 2, respectivamente.
Estudando-se o máximo e o mínimo das expressões (7) e (8), se
encontra:
a) O ângulo que o plano principal 1 faz com o plano de
determinado por:
0
é
0
1
arctg
b) Os valores para
1
e
0
2,
(9)
0
são determinados por:
*
0
*
2
0
1
2
0
(10)
2
*
0
*
2
0
2
2
2
2
2
(11)
c) No plano de 1 e no plano de 2, a tensão de cisalhamento é igual a
zero. Desta forma para que uma tensão normal seja tensão principal,
basta que no plano em que ela atua, a tensão de cisalhamento seja
nula.
d) A tensão de cisalhamento, como a tensão normal, possui um valor de
máximo e um valor de mínimo. Estes valores são determinados por:
0
*
2
0
máx
mín
2
2
(12)
Exemplo.
Em um ponto são conhecidas as tensões
perpendiculares entre si, como mostra a figura V-8.
em
dois
Plano B
50MPa
20MPa
Plano A
15MPa
Figura V-8- Tensões em planos perpendiculares de um estado duplo.
planos
Para este estado de tensões, determinar:
a) As tensões principais
b) A tensão de cisalhamento máxima
c) O plano da tensão 1.
Solução:
As tensões que atuam no plano A são:
A
15MPa
A
20MPa
Como o plano B é perpendicular ao plano A, a tensão de cisalhamento
que nele atua tem o mesmo valor e sinal contrário àquela que atua no plano A.
Com isto, as tensões que atuam neste plano são:
B
B
50MPa
20MPa
De acordo com a expressão (10), é possível escrever:
2
A
1
1
B
A
2
2
A
B
2
15 50
2
1
2
15 50
2
20 2
59,1MPa
2
A
2
2
B
2
A
2
A
B
2
15 50
2
2
15 50
2
2
20 2
5,9MPa
De acordo com a expressão (12) é possível escrever:
2
A
máx
min
máx
2
2
15 50
2
min
máx
2
A
B
min
20 2
26,6MPa
De acordo com a expressão (9), se pode registrar:
arctg
A
1
A
com esta expressão, o ângulo
plano 1. Assim, se tem:
encontrado será o ângulo entre o plano A e o
arctg
15 59,1
20
65,6 o
Plano B
Plano A
Plano 1
,6
65
Plano 2
Figura V-9- Planos principais para o estado duplo da figura 7.