Exercícios Problemas Exercícios Problemas

57
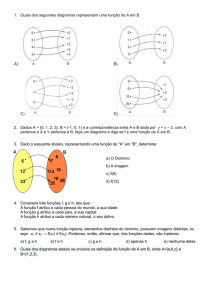
Seja
p
z1 5 cis }}
4
1 2
61
A figura representa, no plano complexo, um octógono regular inscrito numa circunferência de perímetro 6 p .
um número complexo.
E
1 1
C) Verifique se o inverso do número complexo z 5 }} 1 }} i pertence ao conjunto A .
4 4
62
• o simétrico do seu conjugado pertence à bissectriz do primeiro quadrante
e está sobre uma circunferência de raio 5, centrada na origem.
Escreva z na forma trigonométrica.
Defina por uma condição em C as seguintes representações:
B)
63
y
5
3
Considere, no plano complexo, o conjunto
p
3p
A 5 z å C : z. 2 › }} , arg (z 1 i) , }} .
4
4
5
2
1
2
x
O
C)
8
1
z 5 }}}
p
2w
cis }}
5
pertence ao con-
p
w 5 27 cis }} .
2
Justifique que as raízes cúbicas de w pertencem ao conjunto A .
y
64
2
3
A) Averigúe se o número complexo
junto A .
x
4
B) Seja
3
O
6
1cis }p8}2 2 1cis }p8}2
O
–1
D)
y
G
• pertence ao segundo quadrante;
z = r cis u , prove que:
y
H
Acerca de um número complexo z sabe-se que:
sen (n u) . [zn 1 (zw )n] 1 i cos (n u ) . [zn 2 (zw )n] 5 0
A)
x
F
B) Defina por uma condição em C o arco de
circunferência contido no 4.º quadrante.
A 5 {z å C : Im(z1 1 2 1 3i) # Re(z 2 z1) ‹ z 2 3# 2}
59
A
O
A) Determine as coordenadas dos vértices do
octógono.
B) Represente no plano complexo o conjunto
Dado o número complexo
B
O ponto A pertence ao semieixo positivo real.
z
1
A) Resolva, em C , a equação }} 5 }} .
z1
wz
58
03
C
D
2
Exercícios
Problemas
y
Exercícios
Problemas
03
B) Sabendo que z1 é uma das raízes quartas de um complexo z , quais as outras
raízes e o complexo z ?
O
–3
x
x
Considere no plano complexo o ponto P(x , 2x) , imagem geométrica do número
complexo z .
Sejam A , B e C os afixos dos complexos wz , 2 z
e 2 wz .
A) Determine a expressão que dá a área do rectângulo [PABC] .
60
B) Calcule os valores reais de x para os quais a imagem de z pertence ao interior
do círculo centrado na origem e de raio 5 .
Considere, no plano complexo, o conjunto
p
A 5 z å C : 2 }} # arg z # 0 ‹ 2 , z, 3
2
5
6
3
A) Mostre que o número complexo z 5 }}}
p 3
cis }}
conjunto A .
6
1
158
65
5p
^ ik 2 œ2w cis }4}
k521
2
não pertence ao
B) Seja a um número real. Determine o conjunto dos valores que a pode tomar
para que o número complexo w 5 a 1 1 2 (1 2 a) i pertença ao conjunto A .
Seja
A 5 {z å C : z 2 1 2 i, 2 ‹ Re(i z) 5 0} .
A) Represente o conjunto A no plano complexo.
B) Considere o número complexo z 5 (x 2 y 1 1) 1 (x 1 y 1 1) i .
Determine os valores reais de x e y para os quais o complexo z pertence ao
conjunto A .
159