Plano de Aula Aluno(a): Luiz Ambrozi e Derli Santos da Silva Escola

Plano de Aula
Aluno(a):
Luiz Ambrozi e Derli Santos da Silva
Escola: Escola Estadual de Ensino Médio Mestre Santa Bárbara
Disciplina: Matemática
Conteúdo: Função Exponencial
Assunto: Exercícios de função e equação exponencial para reforço
Público alvo: Alunos do 1° ano do
Duração: 7 horas aulas
Ensino Médio
Objetivo: Auxiliar ao aluno a retomar algumas propriedades de função
exponencial e das equações exponenciais, assim conseguindo interpretar de maneira
mais adequada exercícios aplicados envolvendo este conteúdo.
Recursos: Quadro e giz
Desenvolvimento Metodológico:
Inicialmente o professor deve retomar algumas propriedades da função
exponencial e o seu conceito: “ Dado um numero real a ( a>0 e a  1 ), denomina-se
função exponencial de base a uma função f de
em
*

definida por f ( x)  a x ou
y  a x .”
Podemos mostrar alguns exemplos para os alunos poderem identificar:
  y  3x
1
  f ( x)   
2

 2
x
x
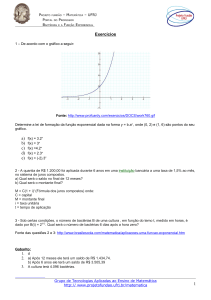
Após retomar o que é uma função exponencial o professor pode fazer a
construção do gráfico da função exponencial, atribuindo valores a variável x. Exemplo:
f ( x)  2 x
X
F(x
)
-2
¼
-1
½
0
1
1
2
2
4
3
8
4
16
Depois de retomarmos a construção do gráfico podemos resolver algumas
equações exponenciais como exemplo, para depois partir nos exercícios de fixação.
Exemplos:
a)3.4 x 1  96
b)2 x  2  2 x 1  18
c)22 x  9.2 x  8  0
Após resolver os exemplos, basta se divertir resolvendo os exercícios que
seguem.
Exercícios:
1 - Resolva as equações a seguir:
a)2.3x 1  6
b)7 x  2.7 x 2  7 x 3  0
c)22 x 1  3.2 x 1  8
d )32 x  3x  6
e)5.2 x
2
4
 160
f )(0,5) 2 x  213 x
1
g ) 5 2x 
32
1
h)  
 16 
x2
 8x
2 - Numa certa cultura de bactérias, há 1000 bactérias num determinado
instante. Após 10 min, existem 4000 mil bactérias. Quantas bactérias existirão em 1h,
sabendo que elas aumentam através da fórmula P  P0 .ekt , em que P é o numero de
bactérias, t é o tempo em horas e k é a taxa de crescimento das bactérias ?
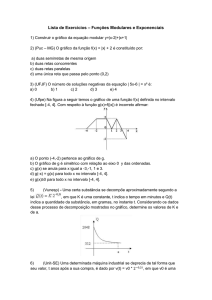
2 x para  1  x  1

3 - Se f ( x)   1
então f(0) - f (3/2) é igual a:
 ,x 1
x
a.
5/2
b.
5/3
c.
1/3
d.
-1/2
e.
-2/3
4 – (PUC - MG) uma população de bactérias começa com 100 e dobra a cada
três horas. Assim, o numero n de bactérias após t horas é dada pela função
t
n(t )  100.2 3 . Nessas condições pode-se afirmar que a população de 51.200 bactérias
depois de:
a)
1 dia e 3horas
b)
1 dia e 9 horas
c)
1 dia e 14 horas
d)
1 dia e 19 horas
5 – Uma colônia de bactérias cresce a um ritmo de 0,5% por hora. Se certa
contagem deu 2000 bactérias, quantas haverá 2 dias depois? Indique uma função que
sirva de modelo a este crescimento.
6 - (UCDB-MS) Certa substância radioativa de massa
M0, no instante t = 0, tende a se transformar em outra substância não radioativa.
Para cada instante t > 0, dado em segundos, a massa da substância radioativa
restante obedece à lei m(t )  m0 (3)2t . Nessas condições, o tempo necessário, em
segundos, para que a massa da substância radioativa seja reduzida a um terço da massa
inicial é igual a:
7- A evolução prevista para a população de uma certa cidade é dada por
t
P  125000.(1.12) 20 , em que t é o numero de anos decorridos após o final de 2003.
a)
Qual seria a população no fim de 2003?
b)
Qual é a população prevista para o fim de 2043?
8 – Uma empresa de computadores fez uma analise das perspectivas de
crescimento e estima que o número de funcionários pode ser escrito pela função
y  300(0,04)0,5 . Sendo y o numero de funcionários após x anos, responda:
x
a)
Com quantos funcionários a empresa começou?
b)
Se as previsões estiverem corretas, quantos funcionários a
empresa terá aproximadamente após 2 anos?
Avaliação: Esta aula foi solicitada pela professora titular da turma e serviu para
retomarmos o conteúdo como preparo para a prova, auxilio a professora com os
exercícios aplicados, pois ela não conseguiu trabalhar em sala de aula, então foram
trabalhados nas aulas de reforço.De certa forma observou-se um pouco de dificuldade
nos exercícios de aplicação, por parte da falta de interpretação do aluno.
Referências bibliográficas:
YOUSSEF,Antonio N.;SOARES, Elizabeth; FERNANDEZ, Vicente P.,
Matemática Ensino Médio, Volume Único, Editora Scipione, 1° Ed., São Paulo, 2009.
DANTE, Luiz R., Matemática Dante Ensino Médio, Volume Único, Editora
Ática, 1° Ed., São Paulo, 2009.
GUELLI, Oscar. Matemática Série Brasil Ensino Médio, Volume Único,
Editora Ática, 1° Ed. São Paulo. 2003
Site:
http://pt.scribd.com/doc/23608526/Lista-de-exercicios-Funcao-
exponencial, acessado em 24 de fevereiro de 2011.
Site: http://www.ebah.com.br/content/ABAAABhcwAD/exercicios-resolvidosmatematica-funcao-exponencial, acessado em 24 de fevereiro de 2011.