b - ProENEM

AULA AO VIVO
Professor Luiz Amaral
EQUAÇÕES E
FUNÇÃO EXPONENCIAL
EQUAÇÕES EXPONENCIAIS
Ex 1 : 2  2  2  2  8
3
Ex 2 : 5  5  5  5  5  625
4
Então, b  b  b  b ... b
n
n fatores
Ex 3 : 2  2  (2  2  2)  (2  2  2  2)  2
3
4
P1 : b  b  b
n
m
n m
7
7 77777
2
Ex 4 : 3 
7
7
777
5
n
b
nm
P2 : m  b
b
Ex 5 : (5  7 )  (5  7 )  (5  7 )  (5  7 ) 
4
2 3
4
2
4
2
5 5 5 7 7 7  5 7
4
4
4
2
2
P3 : (b  a )  b  a
m
n x
mx
x
b  b
Obs.:  n   nx
a
a 
m
mx
nx
2
12
4
6
2
Ex 6 : (7  6  2 )  7  6  2
4
2
5 10
40
20
50
Obs.: (b )  (b )
m n
n m
Ex 7 : (2 )  (2 )  2  4096
4 3
3 4
12
3
3
Ex 8 : 5  5  5  5
3
3
P4  b  b
n
a
a
n
P5  b  1, b  0
0
1
3
2
33
0
Ex 9 : 3  2  2  1
2
0
Obs.: 0 
0
0
FUNÇÃO EXPONENCIAL
DEFINIÇÃO : ƒ :
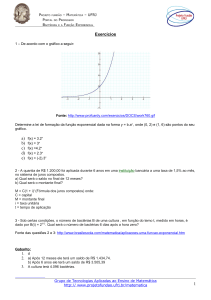
Ex 1 : ƒ (x)  2
 ; f(x)  b ; b  0 e b  1
x
x
1
ƒ (2 ) 
4
1
1
ƒ (2 ) 
2
0
ƒ (2 )  1
2
ƒ (2 )  2
1
ƒ (2 )  4
D
ƒ (2 )  8
Obs.: Se b  1 função crescente!
2
3
Im  (0, )
1
Ex 2 : ƒ (x)   
2
ƒ (2)  4
ƒ (1)  2
ƒ (0)  1
1
ƒ (1) 
2
1
ƒ (2) 
4
x
QUESTÃO 1
Em uma cidade, a população de pessoas é dada por P(t)=Po2t e a população de
ratos é dada por R(t) = Ro4t, sendo o tempo medido em anos. Se em 1992 havia
112000 pessoas e 7000 ratos, em que ano o numero de ratos será igual ao de
pessoas?
RESOLUÇÃO
Po  112000 e Ro  7000
Cálculo de t
112000  2  7000  4
t
t
112  2  7  (2 )
t
2 t
112
2 
7
t
2  16
t
t4
Por tanto, 1992  4  1996
QUESTÃO 2
Considere que num recipiente, no instante t = 0, um número N0 de bactérias estão
se reproduzindo normalmente. É aceito cientificamente que o número de
bactérias num certo instante t > 0 é dado pela equação N(t) = N0Kt , sendo N(t) o
número de bactérias no instante t e K uma constante que depende do tipo de
bactéria. Suponhamos que, num certo instante t = 0, observou-se que havia 200
bactérias no recipiente reproduzindo-se normalmente. Passadas 12 horas, havia
600 bactérias. Após 48 horas do início da observação, quantas bactérias existirão?
RESOLUÇÃO
t  0  200  No  K  No  200
o
t  12  600  200  K  3  K
12
12
t  48  N(48)  200  K  K 
48
N  200  81  16200
48
(K )  3  81
12 4
4