128217267159520_Simulado-A-_-Funcoes-Modular-e

Matemática
Daniel Keglis
1,5
SIMULADO A – Capítulo 5_ Função Modular – Gráfico, Equações Modulares e
Inequações Modulares Capítulo 6 _Função Exponencial – Gráfico, Equações Exponenciais
Leia o simulado com atenção
Não serão permitidas rasuras
Cada acerto tem valor igual a 0,15
1)
O módulo ou valor absoluto de um número
real qualquer terá sempre um resultado:
a) maior do que zero
b) menor do que zero
3) O resultado da
2 x  3  x  5 é igual a:
equação
modular
 2 
,8
 3 
a) S = 
c) igual a zero
d) maior ou igual a zero


2
3
b) S =  8, 
e) menor ou igual a zero
c) S =  8,2
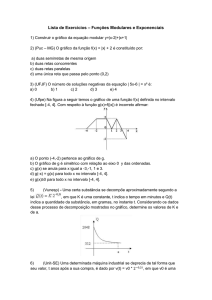
2) A função que melhor representa o gráfico
abaixo é:
 2 
,2
 3 
d) S = 
2 
3 
e) S =  ,8
4) O resultado da inequação |3x +1|  10
solução no intervalo:

11
a)   ,   3,
3

 11 
a) f x   x  1  1
b) f x  x  2  1
c) f x  x  2  1
d) f x  x  2  1
e) f x   x  1  1
b)   ,3
 3 
 11 
c)   ,3
 3 
 11 
d)   ,3
 3 
e)
 ,3
tem
5)
O
resultado
x
5
 25 
   
2
 4 
da
equação
exponencial
x2
8) O
2
resultado
x 3
2
x 1
da equação exponencial
 17 tem solução para:
é igual a:
a) x = 0
b) x = 2
a) 4
c) x = 1
b) 2
d) x = 3
c) – 2
e) x = - 2
d) – 4
e) 0
6) A função que melhor representa o gráfico
abaixo é:
9) Um capital de R$ 2000,00 foi aplicado em um
fundo de renda fixa, em regime de juro
composto, à taxa de 20% ao ano. O tempo
que esse capital deve permanecer aplicado
para que o montante atinja R$ 2880,00 é:
t
(Lembrar que M  C.1  j  , onde, M =
Montante, C = Capital, j = juros e t = tempo)
a) 1,5 anos
b) 2 anos
c) 2,5 anos
d) 3 anos
e) 4 anos
a)
f x   3
b)
1
f x    
 3
c)
f x   2 x
d)
1
f x    
2
x
x
10) A solução da equação
a) x  3
x
e) Nenhuma das anteriores
7) A função n(t )  1000.2 0, 2t indica o número de
bactérias existentes em um recipiente, em
que t é o número de horas decorridas e n(t) a
quantidade de bactérias. Quanto tempo após
o início do experimento haverá 64000
bactérias?
a) 26 horas
b) 27 horas
c) 28 horas
d) 29 horas
e) 30 horas
4
3
3
c) x  
4
4
d) x 
3
3
e) x 
4
b) x  
3
25 x  5 é: