Uma pista retangular para caminhada mede 100 por 250 metros

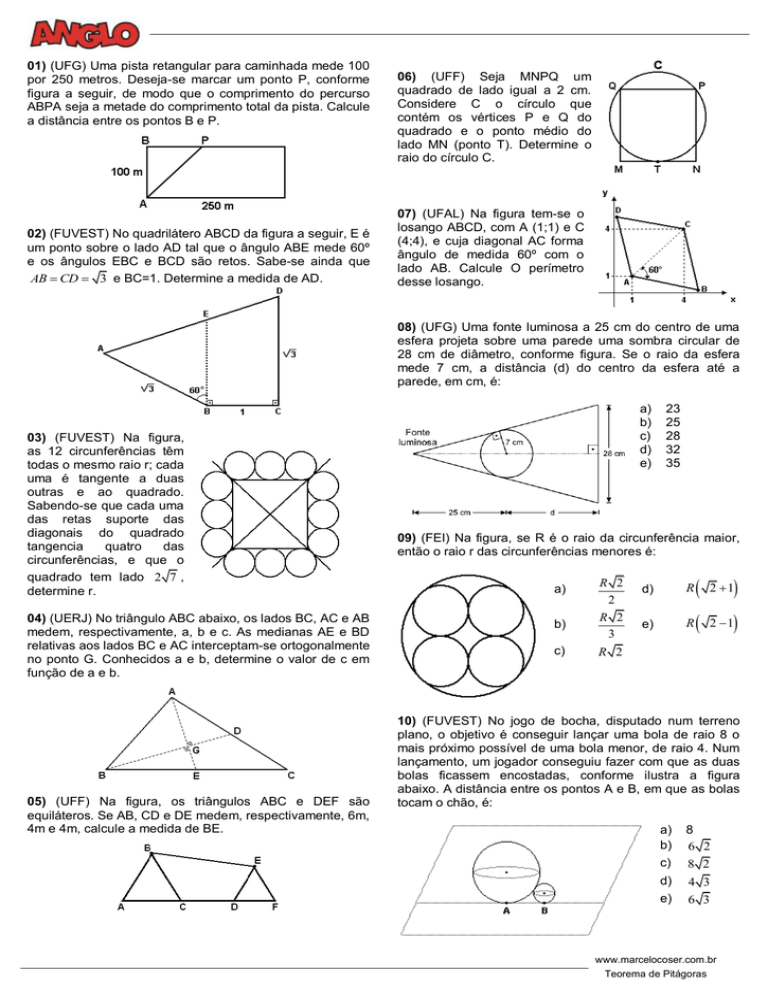
01) (UFG) Uma pista retangular para caminhada mede 100
por 250 metros. Deseja-se marcar um ponto P, conforme
figura a seguir, de modo que o comprimento do percurso
ABPA seja a metade do comprimento total da pista. Calcule
a distância entre os pontos B e P.
02) (FUVEST) No quadrilátero ABCD da figura a seguir, E é
um ponto sobre o lado AD tal que o ângulo ABE mede 60º
e os ângulos EBC e BCD são retos. Sabe-se ainda que
AB  CD  3 e BC=1. Determine a medida de AD.
06) (UFF) Seja MNPQ um
quadrado de lado igual a 2 cm.
Considere C o círculo que
contém os vértices P e Q do
quadrado e o ponto médio do
lado MN (ponto T). Determine o
raio do círculo C.
07) (UFAL) Na figura tem-se o
losango ABCD, com A (1;1) e C
(4;4), e cuja diagonal AC forma
ângulo de medida 60º com o
lado AB. Calcule O perímetro
desse losango.
08) (UFG) Uma fonte luminosa a 25 cm do centro de uma
esfera projeta sobre uma parede uma sombra circular de
28 cm de diâmetro, conforme figura. Se o raio da esfera
mede 7 cm, a distância (d) do centro da esfera até a
parede, em cm, é:
03) (FUVEST) Na figura,
as 12 circunferências têm
todas o mesmo raio r; cada
uma é tangente a duas
outras e ao quadrado.
Sabendo-se que cada uma
das retas suporte das
diagonais do quadrado
tangencia
quatro
das
circunferências, e que o
quadrado tem lado 2 7 ,
determine r.
04) (UERJ) No triângulo ABC abaixo, os lados BC, AC e AB
medem, respectivamente, a, b e c. As medianas AE e BD
relativas aos lados BC e AC interceptam-se ortogonalmente
no ponto G. Conhecidos a e b, determine o valor de c em
função de a e b.
05) (UFF) Na figura, os triângulos ABC e DEF são
equiláteros. Se AB, CD e DE medem, respectivamente, 6m,
4m e 4m, calcule a medida de BE.
a)
b)
c)
d)
e)
23
25
28
32
35
09) (FEI) Na figura, se R é o raio da circunferência maior,
então o raio r das circunferências menores é:
a)
b)
c)
R 2
2
R 2
3
d)
R

2 1

e)
R

2 1

R 2
10) (FUVEST) No jogo de bocha, disputado num terreno
plano, o objetivo é conseguir lançar uma bola de raio 8 o
mais próximo possível de uma bola menor, de raio 4. Num
lançamento, um jogador conseguiu fazer com que as duas
bolas ficassem encostadas, conforme ilustra a figura
abaixo. A distância entre os pontos A e B, em que as bolas
tocam o chão, é:
a)
b)
c)
d)
e)
8
6
8
4
6
2
2
3
3
www.marcelocoser.com.br
Teorema de Pitágoras
11) (FUVEST) Na figura abaixo, a reta s passa pelo ponto
P e pelo centro da circunferência de raio R, interceptando-a
no ponto Q, entre P e o centro. Além disso, a reta t passa
por P, é tangente à circunferência e forma um ângulo 
com a reta s. Se PQ = 2R, então cos  vale:
a)
2
6
d)
2 2
3
b)
2
3
e)
3 2
5
2
c)
2
12) (PUCRJ) A maior distância entre dois pontos de um
retângulo de base 8 cm e altura 6 cm é, em cm:
a)
14
b)
10
c)
7
d)
11
e)
17) (UFPE) Na figura, ABD e BCD são triângulos
retângulos isósceles. Se AD = 4, qual é o comprimento de
DC?
a) 4 2
b) 6
c) 7
d) 8
e) 8 2
18) (UFRRJ) Um arquiteto vai construir um obelisco de
base circular. Serão elevadas sobre essa base duas hastes
triangulares, conforme figura a seguir, onde o ponto 0 é o
centro do círculo de raio 2m e os ângulos BOC e OBC são
iguais. O comprimento do segmento AB é:
a)
b)
c)
12
d)
e)
13) (UEL) Se um círculo de 5 cm de raio está inscrito em
um hexágono regular, o perímetro do hexágono, em
centímetros, é igual a:
a)
20 3
b)
18 3
c)
15 2
d)
12 3
e)
9 2
14) (UFLAVRAS) Qual deve ser a altitude do balão para
que sua distância ao topo do prédio seja de 10km?
a)
b)
c)
d)
e)
6 km
6.200 m
11.200 m
4 km
5 km
15) (UFLAVRAS) Os lados de um triângulo medem 1m, 2m
e 3m. A medida em metros que adicionada aos três lados
transforma o triângulo em um triângulo retângulo é
a)
1m
b)
2m
c)
3m
d)
4m
e)
b)
c)
d)
1
cm
3
1
cm
4
2
cm
2
2
cm
3
19) (UNESP) Em uma residência, há uma área de lazer
com uma piscina redonda de 5 m de diâmetro. Nessa área
há um coqueiro, representado na figura por um ponto Q. Se
a distância de Q (coqueiro) ao ponto de tangência T (da
piscina) é 6 m, a distância d = QP, do coqueiro à piscina, é,
em metros:
a) 4
b) 4,5
c) 5
d) 5,5
e) 6
20) (PUCPR) Quatro triângulos congruentes são recortados
de um retângulo de 11x13. O octógono resultante tem oito
lados iguais. O comprimento do lado deste octógono é:
a)
b)
c)
d)
e)
5m
16) (UFMG) Na figura, estão representadas três
circunferências, tangentes duas a duas, e uma reta
tangente às três circunferências. Sabe-se que o raio de
cada uma das duas circunferências maiores mede 1 cm.
Então, é CORRETO afirmar que a medida do raio da
circunferência menor é:
a)
2m
3m
3 2 m
2 5 m
2 3 m
3
4
5
6
7
21) (UFRGS) Observe a figura. Cada um dos quatro
círculos tem raio igual a 2  1 e é tangente às diagonais
do quadrado e a um de seus lados. A área do quadrado é:
a)
b)
c)
d)
e)
2 1
2 2
4
3 2 1
6
www.marcelocoser.com.br
Teorema de Pitágoras
22) (UFRGS) Dada a figura, qual o valor de x?
a)
b)
c)
d)
e)
2,15
2,35
2,75
3,15
3,35
23) (UFRGS) Na figura, os três círculos têm o mesmo raio
r, as retas são paralelas, os círculos são tangentes entre si
e cada um deles é tangente a uma das duas retas. Dentre
as alternativas abaixo, a melhor aproximação para a
distância entre as retas é
a)
b)
c)
d)
e)
28) (UFRGS) Um hexágono regular tem lado de
comprimento 1. A soma dos quadrados de todas as suas
diagonais é:
3r
3,25r
3,5r
3,75r
4r
a)
24) (FUVEST) Um lenhador empilhou 3 troncos de madeira
num caminhão de largura 2,5 m, conforme a figura abaixo.
Cada tronco é um cilindro reto, cujo raio da base mede 0,5
m. Logo, a altura h, em metros, é
a)
1 7
2
d) 1 
7
3
b)
1 7
3
e) 1 
7
4
1 7
c)
4
25) (CESGRANRIO) Uma folha quadrada de papel ABCD é
dobrada de modo que o vértice C coincide com o ponto M,
médio de AB. Se o lado de ABCD é 1, o comprimento BP é
a)
b)
c)
d)
e)
0,3
0,325
0,375
0,45
0,5
26) (UNIUBEMG) Sejam dois círculos de raios R e r
tangentes no pontos A e ambos tangente ao quadrado de
lado 1, com R >r. Calcule R
32 2
2
b)
c)
2 1
4
d)
e)
2 1
2
a)
27) (FFFCMPA) A companhia telefônica coloca cabos
cilíndricos em dutos cilíndricos. A figura indica a relação
entre as seções transversais de 4 cabos e do menor duto
que pode contê-los. Supondo que o diâmetro de cada cabo
seja 1 cm, o valor mais próximo para o diâmetro do duto
mínimo é de:
a) 2 cm
b) 2,5 cm
c) 3 cm
d) 3,5 cm
e) 4 cm
2 2
2
2 1
3
6
b)
12
c)
18
d)
24
e)
30
29) (UFMG) Observe a figura. ABCD representa um
quadrado de lado 11 e AP = AS = CR = CQ. O perímetro
do quadrilátero PQRS é:
a)
b)
c)
d)
11
22
11
22
3
3
2
2
30) (MACK) A folha de papel retangular na figura I é
dobrada como mostra a figura II. Então, DP mede:
a)
b)
c)
d)
e)
12 5
10 5
8 5
21
25
31) (UFRJ) Na figura, o
triângulo AEC é equilátero e
ABCD é um quadrado de lado
2cm. Calcule a distância BE.
GABARITO
01
105
02
05
09
13
17
21
25
29
2 21
E
A
D
C
C
D
06
10
14
18
22
26
30
7
1,25
C
B
E
C
A
B
03
07
11
15
19
23
27
31
7


2 1
12 2
D
B
A
D
B
6 2
04
08
12
16
20
24
28
a 2  b2
5
A
B
B
C
E
E
www.marcelocoser.com.br
Teorema de Pitágoras