Matemática
Plantão dirigido9° ano ___ Prof.: Magno
Nome:
Nº:
1º trimestre
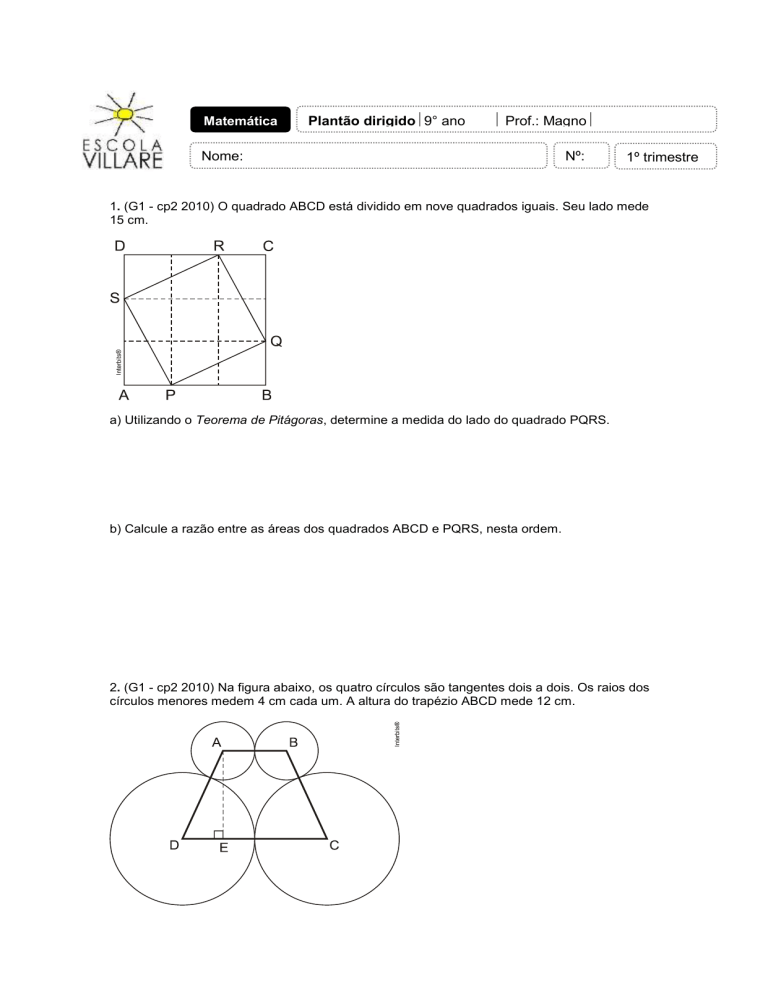
1. (G1 - cp2 2010) O quadrado ABCD está dividido em nove quadrados iguais. Seu lado mede
15 cm.
a) Utilizando o Teorema de Pitágoras, determine a medida do lado do quadrado PQRS.
b) Calcule a razão entre as áreas dos quadrados ABCD e PQRS, nesta ordem.
2. (G1 - cp2 2010) Na figura abaixo, os quatro círculos são tangentes dois a dois. Os raios dos
círculos menores medem 4 cm cada um. A altura do trapézio ABCD mede 12 cm.
a) Simbolizando o raio da circunferência maior por x, determine esse valor, aplicando o
Teorema de Pitágoras aos lados do triângulo ADE.
b) Calcule a medida da área do trapézio ABCD.
3. (G1 - cp2 2008) O quadrilátero ABCD a seguir representa um terreno plano, onde os ângulos
B e D são retos e os lados AD , DC , CB medem 30, 40 e 10 metros, respectivamente.
a) Calcule o valor aproximado do perímetro desse terreno. (Use
6 = 2,44 ).
b) Deseja-se cercar esse terreno com um arame inextensível que custa R$ 32,00 o metro.
Calcule o custo para cercar esse terreno, sabendo que será contornado uma única vez pelo
arame.
4. (G1 - cftmg 2006) A figura mostra o polígono ABCDEF, no qual dois lados consecutivos
quaisquer são perpendiculares. O ponto G está sobre o lado CD e a reta r. As medidas dos
lados AB, BC, EF e FA são, respectivamente, 16 cm, 12 cm, 6 cm e 8 cm.
O perímetro do polígono ABCG, em cm, é
a) 46
b) 48
c) 50
d) 52
5. (G1 - ifce 2014) Na figura abaixo, o valor da área do quadrado de lado “a”, em função dos
segmentos “b” e “c”, é
a) b2 + c2
b) b2 - c2
c) b2c2
d) c2 - b2
e) b2/c2
6. (G1 - ifsp 2014) Ao ligar, por segmentos de retas, os pontos médios dos lados de um
quadrado de lado 60 cm, obtém-se um quadrilátero, cujo perímetro é, em centímetros,
a) 30 2.
b) 60 2.
c) 90 2.
d) 120 2.
e) 150 2.
7. (G1 - ccampos 2011) Abaixo temos um triângulo retângulo ABC e uma figura F composta por
quatro triângulos congruentes a ABC. Considerando que BC = 8 cm e 3 AC = 4 AB , qual é o
perímetro da figura F?
a) 36,0 cm
b) 36,4 cm
c) 38,0 cm
d) 38,4 cm
8. (G1 - ifsp 2014) Um restaurante foi representado em sua planta por um retângulo PQRS.
Um arquiteto dividiu sua área em: cozinha (C), área de atendimento ao público (A) e
estacionamento (E), como mostra a figura abaixo.
Sabendo que P, H e R são colineares, que PH mede 9 m e que SH mede 12 m, a área total
do restaurante, em metros quadrados, é
a) 150.
b) 200.
c) 250.
d) 300.
e) 350.
Gabarito:
1. a) 5√5
2. a) 9
3. a) 128,8m
4. c)
5. a)
6. d)
7. d)
8. d)
b)
9
5
b)156cm²
b) R$ 4.121,60