C:\Documents and Settings\Administrador\Desktop\IUS

TRIÂNGULO
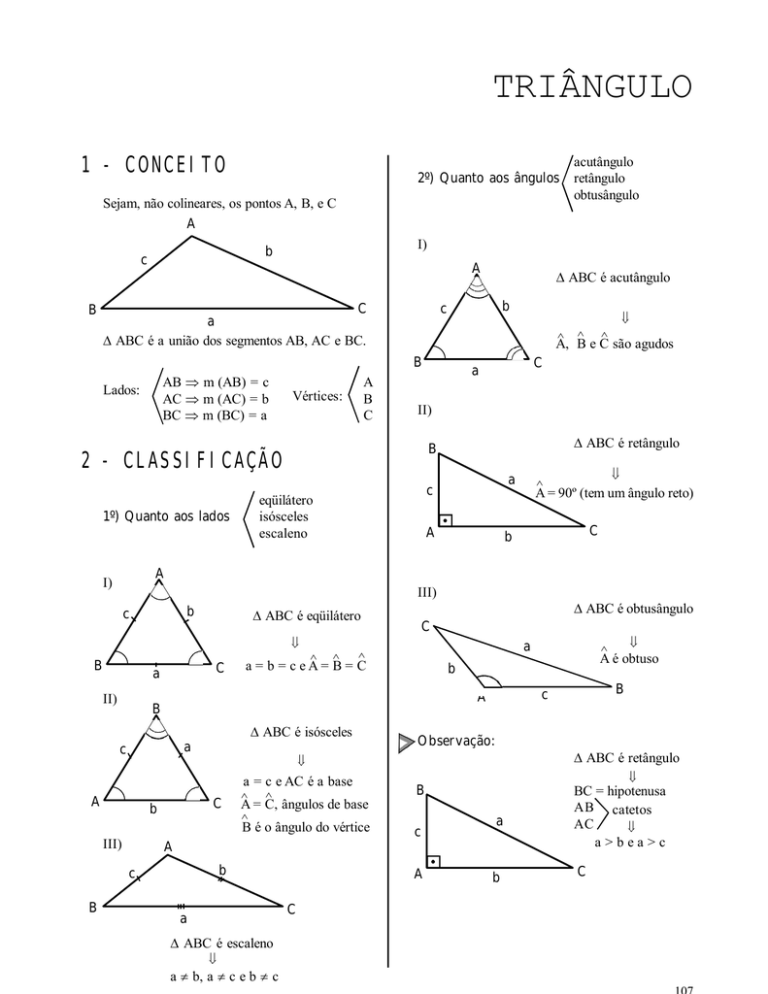
1 - CONCEITO
2º) Quanto aos ângulos
Sejam, não colineares, os pontos A, B, e C
A
B
I)
b
c
A
C
a
∆ ABC é a união dos segmentos AB, AC e BC.
AB ⇒ m (AB) = c
AC ⇒ m (AC) = b
BC ⇒ m (BC) = a
Vértices:
A
B
C
b
^ ^
^ B
A,
e C são agudos
∆ ABC é retângulo
B
a
c
eqüilátero
isósceles
escaleno
A
^
A = 90º (tem um ângulo reto)
C
b
A
I)
III)
B
C
a
II)
∆ ABC é eqüilátero
b
c
a
c
C
b
III)
a = c e AC é a base
^ ângulos de base
^A = C,
^
B é o ângulo do vértice
Observação:
∆ ABC é retângulo
B
c
a
BC = hipotenusa
AB catetos
AC
a>bea>c
b
C
A
b
c
a
∆ ABC é escaleno
a ≠ b, a ≠ c e b ≠ c
A
C
B
c
A
a
^
A é obtuso
b
B
A
∆ ABC é obtusângulo
C
^
^ =C
^=B
a = b = c eA
∆ ABC é isósceles
B
C
a
II)
2 - CLASSIFICAÇÃO
1º) Quanto aos lados
∆ ABC é acutângulo
c
B
Lados:
acutângulo
retângulo
obtusângulo
q Soma das Medidas dos Ângulos Internos
de um Triângulo.
D
β
A
θ
II)
∆ABC é isósceles
C
E
α
a =b ⇒A= B
a≠c e b≠c
a
b
α
β
B
C
A
A≠C e B≠C
B
c
Seja DE // BC .
( ) ( )
m (DÂB) = m (AB̂C) = α (alternos internos)
m EÂC = m AĈB = α (alternos internos)
2 A lados diferentes opõem-se ângulos diferentes.
α + θ + β = 180º ou  + B̂ + Ĉ = 180 º
III)
C
Logo, a soma das medidas dos ângulos internos de
qualquer triângulo é igual a 180º.
a
b
q Ângulo Externo de um Triângulo.
A
Ângulo externo de um triângulo, relativo a determinado vértice, é formado por um lado do triângulo e pelo
prolongamento do outro lado.
c
B
∆ ABC é um triângulo retângulo
A
^ ^
a >b ⇒A> B
^ ^
a > c ⇒A> C
e
B
C
3 Ao maior lado opôe-se o maior ângulo.
E
AB̂E é o ângulo externo relativo ao vértice B.
Propriedade do ângulo externo
A medida do ângulo externo é igual à soma das
medidas dos ângulos internos não adjacentes.
As proposições recíprocas de 1 , 2 e 3 são
verdadeiras.
IV)
A
c
ê = Â + Ĉ
3 - DESIGUALDADES EM
TRIÂNGULOS
I)
C
a
b
∆ ABC é equilátero
A
c
B
a = b = c ⇒ A = B = C = 60º
1 A lados iguais opôem-se ângulos iguais
B
a
Seja um triângulo qualquer o ∆ ABC
a < b + c ou a > b - c
b
b < a + c ou b > a - c
c < a + b ou c > a - b
C
4 - ELEMENTOS DE UM
TRIÂNGULO
Alturas (ortocentro)
Medianas (baricentro)
Mediatrizes (circuncentro)
Bissetrizes (incentro)
I)
A
h
B
∆ ABC
IV)
A
BAS ≡ CAS
C
H
Semi-reta AS é a bissetriz do
AH é perpendicular a BC
ângulo interno A do triângulo.
B
AH = h é a altura relativa ao lado BC.
As três alturas de um triângulo se interceptam num
mesmo ponto, denominado de ORTOCENTRO do
triângulo.
II)
C
S
As três bissetrizes de um triâgulo se interceptam
num mesmo ponto, denominado INCENTRO do
triângulo.
A
B
5 - CONGRUÊNCIA DE
TRIÂNGULOS
C
M
q Definição
Sendo BM = MC
AM é a mediana relativa ao lado BC
As três medianas de um triângulo se interceptam
num mesmo ponto, denominado de BARICENTRO
do triângulo.
Propriedade do baricentro de um triângulo.
A
GM
AG = 2GM
∆ ABC ≡ ∆ A1B1C1 ⇔
= 32
AM
1
AG = 3 AM
B
A
C1
B1
C
M
Seja G o baricentro do ∆ ABC
III)
C
B
G
B
Dois triângulo são congruentes se, e somente se,
três lados os três ângulos de um deles forem ordenadamente congruentes aos três lados e aos três ângulos do
outro triângulo.
A1
A
^ ^ ^ ^
^ ^
A ≡ A1, B ≡ B 1 e C ≡ C 1
Casos de congruência de triângulos (condições mínimas para concluir que dois triângulos são congruentes).
1º Caso – LAL
r
C
M
“Se dois triângulos têm ordenadamente congruentes
dois lados e o ângulo compreendido entre eles, então
estes triângulos são congruentes.”
A
)
∆ ABC
BM = MC e r
AB ≡ A1B1, AC ≡ A1C1 e BC ≡ B 1C1
BC
r é a reta mediatriz do ∆ ABC, relativa ao lado BC.
As três mediatrizes de um triângulo se interceptam
num mesmo ponto, denominado CIRCUNCENTRO
do triângulo.
B
C
Esquema do 3º Caso:
A'
)
C'
B'
AB ≡ A ' B' 
 LLL
AC ≡ A ' C' → ∆ ABC ≡ ∆ A 'B ' C '⇒

BC ≡ B' C' 
Â ≡ Â '

B̂ ≡ B̂'

Ĉ ≡ Ĉ'
4º Caso – LAA
Esquema do 1º caso:
“Se dois triângulos têm ordenadamente congruentes
um lado, um ângulo adjacente e o ângulo oposto a esse
lado, então estes triângulos são congruentes.”
A
))
AB ≡ A' B' 
 B̂ ≡ B̂ '
 LAL

 ≡ Â
 → ∆ ABC ≡ ∆ A ' B' C'  BC ≡ B ' C '

 Ĉ ≡ Ĉ
AC ≡ A' C'


2º Caso – ALA
“Se dois triângulos têm ordenadamente congruentes
um lado e os dois ângulos a ele adjacentes, então estes
triângulos são congruentes”.
)
C
B
A'
))
A
)
)
C'
B'
C
B
Esquema do 4º Caso:
A'
)
C'
B'
1) Esquema do 2º caso.

 AB ≡ A ' B '


ALA
BC ≡ B' C' 
→ ∆ ABC ≡ ∆ A 'B ' C '  Â ≡ Â '
 AC ≡ A ' C '

Ĉ ≡ Ĉ '


B̂ ≡ B̂'
3º Caso – LLL
 AB ≡ A ' B'
BC ≡ B' C'

 LAA ∆ ABC ≡ ∆ A 'B ' C ⇒
'  AC ≡ A ' C'
B̂ ≡ B̂'
 →


 ≡  ' 
Ĉ ≡ Ĉ'

EXERCÍCIOS
RESOLVIDOS
01) Em um triângulo isósceles, o ângulo do vértice é
igual à oitava parte do ângulo obtuso formado pelas
bissetrizes dos ângulos da base.
Determine a medida do âgulo do vértice.
“Se dois triângulos têm ordenadamente congruentes
os três lados, então estes triângulos são congruentes.”
Solução:
C
x
a
)
8
x
a
B
A
C'
b
b
a + b + x = 180º ⇒ 2a + 2b = 360º - 2x
2a + 2b + x/8= 180º ⇒ 360º - 2x + x/8 = 180º
⇓
x = 96º
)
A'
Ângulo do vértice: 96º ÷ 8 = 12º
B'
Resp.) 12º
02) O ângulo externo do vértice de um triângulo isósceles
mede 150º.
Determine os ângulos internos do triângulo.
05) Na figura, calcule o ângulo que a altura relativa ao
lado AC forma com a bissetriz interna do ângulo C.
B
Solução:
150º
50 º
y
Resp.) 60º
06) Dois ângulos internos de um triângulo medem 42º e
96º. Determine a medida do terceiro ângulo desse
triângulo.
03) O triângulo ACD da figura é isósceles de base AD.
Sendo m (BAD) = 42º e m (ABC) = 20º, determine
a medida da ângulo ACD.
C
D
A
B
x
D
20 º
42 º
Solução:
terceiro ângulo tem medida x
x + 42º + 96º = 180º
⇓
x = 42º
Resp.) 42º
07) As medidas dos três ângulos internos de um triângulo são expressas por x, x + 10º e x + 20º. Determine as medidas desses três ângulos.
Solução:
x + x + 10 + x + 20 = 180
3x = 150 e x = 50º
x
B
x = 42º + 20º ⇒ x = 62º
e
C
⇓
Resp.) 30º, 75º e 75º
m (ACD) = y
2x + y = 180º ⇒ y = 56º
Resp.) 56º
04) Dois lados de um triângulo medem respectivamente 8cm e 21cm. Sendo a medida do terceiro lado
múltiplo de 6 e de 9 simultaneamente, determine
essa medida.
x = 50º
x + 10º = 60º
x + 20º = 70º
Resp.) 50º, 60º e 70º
08) Um dos ângulos externos de um triângulo mede
45º e os internos não adjacentes a ele são tais que a
medida de um deles é o dobro da medida do outro.
Detemine as medidas dos três ângulos internos desse
triângulo.
Solução:
Solução:
45º
y
Lados: 8cm, 21cm e xcm
x < 8 + 21
e
x > 21 - 8
⇓
⇓
x < 29
x > 13
Múltiplo de 6 e 9 entre 13 e 29 é 18.
Resp.) 18cm
120º
x = 60º
2y = 150º ⇒ y = 75º
A
30 º
30 º
H
x + 90º + 30º = 180º
⇓
C
y
x
A
x + 150º = 180º ⇒ x = 30º
2y + x = 180º
Solução:
C
B
x
y
120º
50º
A
Solução:
x
2x
x + 2x = 45º ⇒ x = 15º e 2x = 30º
y = 180º - 45º ⇒ y = 135º
Resp.) 15º, 30º e 135º
09) Considere o triângulo ABC da figura.
A
D
50º
EXERCÍCIOS
PROPOSTOS
B
C
Se a bissetriz intena do ângulo B̂ , forma com a bissetriz
externa do ângulo Ĉ , um ângulo de 50º, determine a
medida do ângulo interno  .
01) O ângulo do vértice de um triângulo isósceles mede
100º. Determine a medida do ângulo formado pelas
bissetrizes dos ângulos da base e oposto à base.
Resp.) 140º
02) Observe a figura
B
Solução:
A
55 º
D
θ
30 º
50º
y
x
B
x
40 º
A
y
C
y
x
E
Determine o valor de (x + y)
C
Resp.) 195º
∆ DCB ⇒ y = x + 50º 1
∆ ABC ⇒ 2y = 2x + θ 2
03) Um ângulo externo da base de um triângulo isósceles é igual aos 5 4 do ângulo do vértice desse
triângulo.
Substituindo 1 em 2
⇓
2(x + 50º) = 2x + θ
⇓
2x + 100º = 2x + θ ⇒ θ =100º
Calcule os ângulos desse triângulo.
Resp.) 120º, 30º e 30º
Resp.) 100º
10) Calcule o ângulo  da figura, sabendo que as
bissetrizes dos ângulos de vértices B e C formam
um ângulo de 110º
A
04) Na figura, determine a medida do ângulo α em
função de m.
3m
2m
α
m
Resp.) 6m
110º
110º
B
C
Solução:
05) Se dois lados de um triângulo isósceles medem 38cm
e 14cm, determine a medida do terceiro lado desse
triângulo.
Resp.) 38cm
A
θ
06) O lado AB de um triângulo ABC é expresso por
um número inteiro.
110º
x
x
B
110º
Determine o seu valor máximo sabendo que os lados AC e BC medem respectivamente 27cm e 16cm
y
y
C
x + y + 110º = 180º ⇒ x + y = 70º
2x + 2y + θ = 180º ⇒ 2(x + y) + θ = 180º ⇒ θ =40º
Resp.) 40º
e que C < A < B.
Resp.) 15cm
07) Na figura, o triângulo ABC é congruente ao triângulo CDE. Determine o valor de α e β .
E
11) Num triângulo isósceles o semi-perímetro vale 7,5m.
Calcular os lados desse triângulo, sabendo-se que
a soma dos lados congruentes é o quádruplo da
base.
)
5β
C
2α + 10o
))
A
Resp.) 3m, 6m e 6m
)) 3α
D
TESTES
01) Na figura AC = CB = BD e A = 25º
D
)
← β + 48o
B
C
Resp.) α = 10º e β = 12º
08) Na figura abaixo, o triângulo ABD é congruente ao
triângulo CBD. Calcular x e y.
D
B
O ângulo x mede:
a) 50º
b) 60º
c) 70º
d) 75º
3y + 8
2x
02) Na figura AB = BC e AD = BD
A
x
Resp.) 16 e 8
B
2y
60º
))
35
)
3y + 5
x
C
D
O ângulo x mede:
a) 50º
b) 30º
c) 20º
d) 10º
03) Observe a figura.
))
C
A
C
09) Na figura, o triângulo ABC é congruente ao triângulo CDE. Determine o valor de x e y e a razão
entre os perímetros desses triângulos.
B
E
22
2x - 6
A
x
25º
A
D
50 º
Resp.) 14, 10 e 1
10 º
40 º
x
10) Na figura abaixo, os triângulos ABC e CDA são
congruentes. Calcular x e y.
A
)
D
)
27o
120o
Resp.) 60º e 9º
)
B
)
2x
3y
C
O ângulo x mede:
a) 90º
b) 100º
c) 120º
d) 140º
B
04) Na figura triângulo ABC é isósceles de base BC e
A = 80º
A
x
B
08) Num triângulo retângulo que tem um ângulo agudo
medindo 60º, a medida do ângulo formado entre a
bissetriz do ângulo reto e a mediana relativa à
hipotenusa, é:
a) 10º
b) 15º
c) 25º
d) 30º
C
A medida do ângulo x entre as bissetrizes dos ângulos da base, é:
a) 130º
b) 120º
c) 110º
d) 100º
05) A mediana relativa à hipotenusa de um triângulo
retângulo mede:
a) 1/3 da hipotenusa
b) 1/2 da hipotenusa
c) 1/4 da hipotenusa
d) 2/3 da hipotenusa
06) Na figura AM é mediana do triângulo retângulo
ABC
em A, e B = 26º
10) Dois lados de um triângulo medem 12cm e 21cm.
O menor valor inteiro do terceiro lado desse triângulo, em cm, é:
a) 33
b) 32
c) 10
d) 9
11) Num triângulo ABC, AB = 15, BC 7 e AC é múltiplo de 9. Então, entre os ângulos A, B e C, pode-se
afirmar que:
A
B
09) A hipotenusa BC do triângulo retângulo ABC, mede
30cm. Os pontos M e N são pontos médios dos
lados AB e BC, respectivamente. A medida de AN,
em cm, é:
a) 10
b) 12
c) 15
d) 20
C
M
a) A > C
c) B > C
b) A > B
d) B > A
12) No triângulo ABC de lados inteiros, A < B < C. Se
AB = 7cm e BC = 4cm, a soma das possíveis medidas de AC, em cm, é:
a) 5
b) 6
c) 11
d) 15
O ângulo AMC mede:
a) 128º
b) 104º
c) 64º
d) 52º
07) Observe a figura.
A
13) Na figura, BC = CA = AD = DE.
x
A
20 º
B
M
H
C
40 º
40 º
O ângulo x formado pela altura e a mediana relativa à hipotenusa do triângulo retângulo, mede:
a) 30º
b) 40º
c) 50º
d) 60º
B
C
O ângulo CAD mede:
a) 10º
b) 20º
c) 30º
d) 40º
D
E
14) Num triângulo ABC, com A obtuso, os lados AB e
AC medem 3 e 4 respectivamente. Então:
a) BC < 4
b) BC < 5
c) BC < 7
d) 5 < BC < 7
20)
15) Dois lados de um triângulo isósceles medem respectivamente, 5cm e 2cm
O perimetro desse triângulo, em cm, é:
a) 14
b) 12
c) 9
d) 7
16) Num triângulo ABC, A obtuso, os lados AB e AC
medem 6 e 2 respectivamente. Então, a medida x
do lado BC, pertence ao conjunto:
a) { 7}
b) { 8 }
c) { 9,10 }
d) { 5,6 }
17) O primeiro ângulo de um triângulo mede (5x + 3)º,
o segundo (3x + 5)º e a medida de um ângulo externo pelo terceiro vértice é 120º. A diferença entre o
primeiro e o segundo ângulo é:
a) 14º
b) 26º
c) 47º
d) 73º
21) Na figura, a = 100º e b = 110º. A medida x, é:
x
a
b
a) 30º
b) 50º
c) 80º
d) 100º
22) Na figura, r é bissetriz do ângulo AB̂C , α = 40º e β = 30º
B
18) Na figura, AC = BD, AB = BE e α = β
C
x
E
D
A
β
α
A
B
Então:
a) BC = DE
b) BC =
3
2
DE
c) BC =
4
3
DE
d) BC = 2 . DE
19)
β
α
C
r
A medida do ângulo x, é:
a) 20º
b) 15º
c) 10º
d) 5º
GABARITO
01)
06)
11)
16)
21)
D
D
D
A
A
02)
07)
12)
17)
22)
C
C
C
B
D
03)
08)
13)
18)
B
B
B
A
04) A
09) C
14) D
19)
05) B
10) C
15) B
20)