Apresentação 5

Sistemas Elétricos
Indutor
di
v=L
dt
1
i = ∫ v dt
L
Capacitor
v=
q
C
dv 1 dq
=
dt C dt
i=
dq
dt
i=C
dv
dt
q = ∫ i dt
v=
1
i dt
∫
C
Sistemas Elétricos
Resistor
v=Ri
Bloco
Equação (a)
Equação (b)
Armazenamento de energia
Indutor
Capacitor
v=L
v=
di
dt
1
i dt
C∫
1
v dt
∫
L
dv
i=C
dt
i=
Dissipação de energia
Resistor
v=Ri
i=
v
R
Construindo um Modelo para um
Sistema Elétrico
Conservação da carga elétrica
Leis de Kirchoff
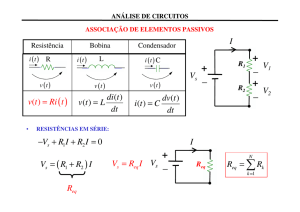
1a lei: A soma algébrica das correntes nos nós é zero.
2a lei: Em um circuito fechado, a soma algébrica das
diferenças de potencial em cada elemento é igual à
força eletromotriz aplicada.
Primeira Lei de Kirchoff
i1 = i2 + i3
A corrente que passa por R1 é i1, e a tensão neste resistor é (v-vA); assim
i1 R1 = v − v A
A corrente em R2 é i2; e como a diferença de potencial em R2 é vA; então
i2 R2 = v A
A corrente i3 passa em R3 em série com R4 e existe uma diferença de
potencial vA sobre a combinação. Assim:
i3 (R3 + R4 ) = v A
Equacionando as correntes, temos:
v − vA vA
vA
=
+
R1
R2 R3 + R4
Segunda Lei de Kirchoff
∑v = 0
Para a malha com corrente i1 circulando, se a corrente em R1 é i1 e em R2 é
(i1 -i3 );
v = i1 R1 + (i1 − i3 )R2
(a)
v = i1 ( R1 + R2 ) − i3 R2
Para a malha com corrente i3 circulando, já que não existe nenhuma fem:
0 = i3 R3 + i3 R4 + (i3 − i1 ) R2
Rearranjando temos
i3 ( R3 + R4 + R2 ) = i1 R2
Substituindo i3 na equação (a)
i1 R22
v = i1 ( R1 + R2 ) −
R3 + R4 + R2
i1 ( R1 R3 + R1 R4 + R1 R2 + R2 R3 + R2 R4 )
v=
R3 + R4 + R2
Em geral, quando o número de nós é menor que o número
de malhas, é mais fácil usar a análise nodal
SISTEMA ELÉTRICO SIMPLES
v = vR + vC
v = iR + vC
dvc
v = RC
+ vC
dt
Sistema resistor-capacitor
vR = iR
dvC
i=C
dt
Dá a relação entre a
saída vc e a entrada v
v = vR + vL + vC
Sistema resistor-indutor-capacitor
mas
dvc
i=C
dt
⇒
di
v = iR + L + vC
dt
d (dvC dt )
d 2 vC
di
=C
=C 2
dt
dt
dt
portanto
dvc
d 2 vC
v = RC
+ LC 2 + vC
dt
dt
Sistema elétrico com duas malhas
(a) Análise nodal
i1 R1 = v − v A
No nó A
i1 = i2 + i3
dv
i3 = C1 A
dt
dvC
dv
v − vA
= C2
+ C1 A
dt
R1
dt
dvC
i2 = C2
dt
(b)
A diferença de potencial na combinação de R2 e C2 é vA, então:
v A = i2 R2 + vC
dvC
⇒ v A = R2C2
+ vC
dt
d 2 vC dvC
dv A
= R2C2
+
2
dt
dt
dt
Substituindo vA e dvA/dt na equação (b)
d 2 vC  R1C1 + R1C2 + R2C2  dvC
v

+ 
+ vC =
2
R1 R2C1C2
dt
R1 R2C1C2

 dt
(b) Análise de malha
Resolver para a próxima aula
Exemplo:
Determinar a relação entre a saída, a diferença de potencial no indutor vL,
e a entrada v para o circuito mostrado na figura
v = vR + vL
v = iR + vL
No Indutor
i=
R
v = ∫ vL dt + vL
L
1
vL dt
∫
L
Exercício para a próxima aula:
Determinar a relação entre a saída, a diferença de potencial no capacitor
vC e a entrada v para o circuito mostrado na figura
A solução pose ser obtida tanto pela análise nodal quanto pela análise de
malha.
Este exercícios terão peso importante na avaliação final
Analogia de Sistemas Mecânicos com
Sistemas Elétricos
Resistor
v
i=
R
Amortecedor F = cv
Grandezas análogas:
•Corrente ⇔ Força
•Diferença de potencial ⇔ Velocidade
•Constante de amortecimento c ⇔ Inverso da resistência 1/R
Bloco
Equação
Const. Análoga
Armazenamento de energia
Indutor
i=
1
v dt
∫
L
1
L
Mola translacional
F = kx = k ∫ v dt
k
Mola torcional
T = kθ = k ∫ ω dt
k
Capacitor
Massa
Momento de inércia
i=C
dv
dt
d 2x
dv
F =m 2 =m
dt
dt
d 2θ
dω
T=J 2 =J
dt
dt
C
m
J
Dissipação de energia
Resistor
i=
v
R
1
R
Amortecedor translacional
F = cv
c
Amortecedor rotacional
T = cω
c
Considere a analogia elétrica para duas molas em série
F1 = F2
Sistema mecânico (molas)
Equivalente elétrico
i1 = i2
Considere a analogia elétrica para duas molas em paralelo
Sistema mecânico (molas)
Equivalente elétrico
F = F1 + F2
i = i1 + i2
Sistema envolvendo uma mola e uma massa
Sistema mecânico
F = ∑ Forças exercidas pela mola + ∑ Forças que agem na massa
Equivalente elétrico
i = Corrente no indutor + Corrente no capacitor
Sistema envolvendo uma mola, um amortecedor e uma massa
Sistema mecânico
F = ∑ Forças exercidas pela mola + ∑ Forças que agem na massa +
Força exercida pelo amortecedo r
Equivalente elétrico
i = Corrente no indutor + Corrente no capacitor +
Corrente no resistor
Exercício para a próxima aula:
Desenhar um circuito elétrico análogo ao sistema mostrado na Figura
Este exercícios terão peso importante na avaliação final