caderno de exercícios 1e

CADERNO DE EXERCÍCIOS 1E
Ensino Médio – Ciências da Natureza I
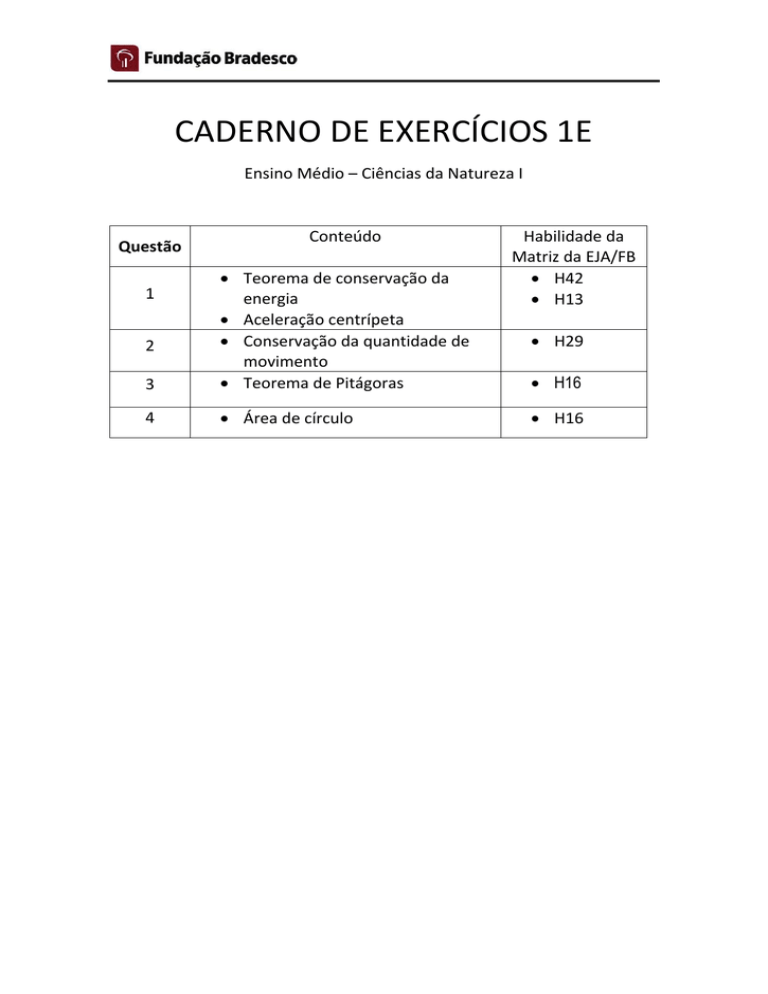
Questão
Conteúdo
3
 Teorema de conservação da
energia
 Aceleração centrípeta
 Conservação da quantidade de
movimento
 Teorema de Pitágoras
4
 Área de círculo
1
2
Habilidade da
Matriz da EJA/FB
 H42
 H13
 H29
 H16
 H16
1. (Unicamp - 2009) Um carrinho de massa m = 300 kg percorre uma montanha russa cujo
trecho BCD é um arco de circunferência de raio r = 5,4 m, conforme a figura adiante.
A velocidade do carrinho no ponto A é vA = 12 m/s. Considerando g = 10 m/s2 e desprezando
o atrito, calcule
a) a velocidade do carrinho no ponto C.
b) a aceleração do carrinho no ponto C.
2. (Enem – 2014) O pêndulo de Newton pode ser constituído por cinco pêndulos idênticos
suspensos em um mesmo suporte. Em um dado instante, as esferas de três pêndulos são
deslocadas para a esquerda e liberadas, deslocando-se para a direita e colidindo elasticamente
com as outras duas esferas, que inicialmente estavam paradas.
O movimento dos pêndulos após a primeira colisão está representado em
a)
c)
e)
b)
d)
3. Ao receber o desenho do projeto de uma escada, um mestre de obra observou que as medidas
da altura dos degraus não estavam informadas. Porém, como ele tem conhecimento sobre
alguns conceitos matemáticos, logo percebeu que não seria difícil encontrar as medidas que
faltavam.
Observe a seguir o projeto que o mestre de obra recebeu.

0,8 m
Considerando que todos os degraus têm a mesma altura, ao utilizar seus conhecimentos, o
mestre de obra encontrou como medida da altura de cada degrau o valor de
a) 15 cm.
b) 60 cm.
c) 32 cm.
d) 33 cm.
e) 5 cm.
Caro aluno,
O próximo exercício também é objetivo e apresenta apenas 4 alternativas, sendo
portanto, diferente do modelo de avaliação à qual você é submetido, em que cada exercício
apresenta 5 alternativas. Porém, consideramos que o exercício apresentado traz uma
abordagem que pode contribuir significativamente para o seu processo de aprendizagem. Por
isso, as divergências observadas entre as estruturas mencionadas foram consideradas
secundárias, já que não impactam na proposta desse material, que é a revisão dos conteúdos
que você está com dificuldades
4. (UNICAMP – 2012) Um vulcão que entrou em erupção gerou uma nuvem de cinzas que atingiu
rapidamente a cidade de Rio Grande, a 40 km de distância. Os voos com destino a cidades
situadas em uma região circular com centro no vulcão e com raio 25% maior que a distância
entre o vulcão e Rio Grande foram cancelados. Nesse caso, a área da região que deixou de
receber voos é
a) maior que 10000 km2.
b) menor que 8000 km2.
c) maior que 8000 km2 e menor que 9000 km2.
d) maior que 9000 km2 e menor que 10000 km2.
Gabarito comentado
1.
a) Para determinarmos a velocidade do carrinho na posição C, utilizaremos o Teorema de
conservação da energia, comparando as posições A e C.
Pelo Teorema de conservação da energia:
Energia mecânica na posição A = Energia mecânica na posição C
Lembrando que:
Energia mecânica = Energia cinética + Energia potencial
Teremos
Energia mecânica na posição A = Energia mecânica na posição C
(Energia cinética + Energia potencial)A = (Energia cinética + Energia potencial)C
(m.v2 + m.g.h)A = (m.v2 + m.g.h)C
2
2
Para a posição A teremos
v = 12 m/s
m = 300 kg
g = 10 m/s2
h=0
Para a posição C teremos:
v=?
m = 300 kg
g = 10 m/s2
h = raio da circunferência = 5,4 m
Substituindo os valores nas expressões acima teremos:
(m.v2 + m.g.h)A = (m.v2 + m.g.h)C
2
2
(300.122 + 300.10.0)A = (300.v2 + 300.10.5,4)C
2
2
(150x144 + 0)A = (150v2 + 16.200)C
21.600 = (150 v2 + 16.200)C
21.600 – 16.200 = (150v2)C
5.400 = (150v2)C
5.400 = (v2)C
150
(v2)C = 36
E extraindo a raiz quadrada de 36 encontramos a velocidade no ponto C
vC = 6 m/s
b) No trecho BCD o carrinho está em um movimento circular. Sua aceleração nesse trecho pode
ser determinada pela expressão:
Aceleração centrípeta = (velocidade)2
Raio
Especificamente para a posição C na qual determinou-se a velocidade no tópico anterior
teremos:
Aceleração centrípeta (ac) na posição C = (velocidade)2 na posição C
Raio
Teremos então
vc = 6 m/s
Raio = 5,4 m
a c = 62
5,4
ac = 6,7 m/s2
2. Nas colisões há conservação da quantidade de movimento. Além disso, como as colisões são
elásticas, a energia cinética se conserva. Estas condições são verificadas na alternativa C,
considerando que a velocidade com que as três esferas incidem é igual à velocidade das três
esferas que partem imediatamente após a colisão.
3. Alternativa A.
Para encontrar a medida da altura de cada degrau, será utilizado o teorema de Pitágoras, já que
a estrutura utilizada para a construção da escada tem o formato de um triângulo retângulo.
Nesse triângulo, é conhecido o valor da hipotenusa e de um dos catetos, logo, para encontrar a
altura dos degraus deve-se calcular a medida do outro cateto.
Pelo teorema de Pitágoras temos:
a² = b² + c²
Lembre-se: as variáveis “b” e “c” representam as medidas dos catetos e a variável “a” representa
a medida da hipotenusa.
(1,0)² = (0,8)² + c²
1,0 = 0,64 + c²
1,0 – 0,64 = c²
0,36 = c²
0,36 = c²
0,6 = c
Se a medida do cateto é igual a 0,6 m, ou 60 cm, para saber a altura de cada degrau basta dividir
essa medida por 4, pois há na escada 4 degraus.
60: 4 = 15
Portanto, cada degrau terá uma altura de 15 cm.
4. Alternativa B.
Para que seja encontrada a área da região que deixou de receber voos, primeiramente devemos
calcular qual é o raio dessa região circular. Para tanto, deve-se lembrar que, segundo informado,
o raio será 25% maior que a distância entre o vulcão e a cidade de Rio Grande. Nesse caso,
calcula-se quanto representa 25% de 40 km.
25
x 40 = 10
100
Logo, o raio dessa região circular terá medida igual a 50 km.
Sendo conhecido o raio, será realizado o cálculo da área da região.
𝐴 = 𝜋𝑟 2
A = 3,14. 50²
A = 3,14. 2.500
A = 7.850 km²