Capítulo 7: Equações Diferenciais Ordinárias

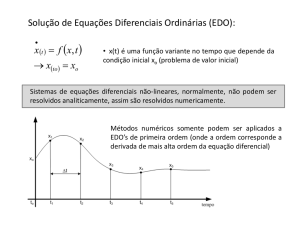
Capítulo 7: Equações Diferenciais Ordinárias
1. Problema de valor inicial
Definição: Seja y uma função de x e n um número inteiro positivo, então uma relação
de igualdade que envolva x, y, y’, y’’,...,y(n) é chamada uma equação diferencial ordinária.
Exemplos
Equação Diferencial
y’=2x
3
d2y
⎛ dy ⎞
+ x 2 ⎜ ⎟ − 15 y = 0
2
dx
⎝ dx ⎠
(y’’’)4-x2(y’’)5+4xy=xex
x3
3
dy ⎛ d y ⎞
⎟ −1
=⎜
dx ⎜⎝ dx 4 ⎟⎠
4
Ordem
1
2
3
4
Uma função f é solução de uma equação diferencial se a substituição de y por f resulta
em uma identidade para todo x em algum intervalo.
Por exemplo, a equação diferencial
y’=6x2-5
tem solução
f(x)=2x3-5x+C
para todo o real C, pois a substituição de y por f conduz à identidade
6x2-5=6x2-5
Denominamos
f(x)=2x3-5x+C
a solução geral de
y’=6x2-5,
pois toda a solução da equação é desta forma. Obtém-se uma solução particular
atribuindo a C valores específicos. Para ilustrar, se C =0, temos a solução particular
f(x)=2x3-5x
Às vezes, impõem-se condições iniciais que determinam uma solução particular.
1
Associados a y(n)=f(x, y’, y’’,...,y(n-1)), podem existir condições cujo número coincide
com a ordem da equação diferencial ordinária. Se tais condições se referem a um único x,
tem-se um problema de valor inicial ⎯ PVI. Caso, contrário tem-se um problema de
fronteira. Por exemplo,
⎧ y ' ' = 3 y '−2 y
⎪
⎨ y (0) = −1
⎪ y ' (0) = 0
⎩
é um PVI de segunda ordem.
Pretende-se valores de y(x) em pontos distintos daqueles das condições iniciais
associadas aos PVI. Vai se estudar PVI de primeira ordem, i.e.,
⎧ y ' = f ( x, y )
, ηum número dado. (7.1)
⎨
⎩ y ( x0 ) = y 0 = η
Os PVI de ordem superior a um podem ser reduzidos a sistemas de PVI de primeira
ordem à custa de variáveis auxiliares.
Exemplo
Considere-se o seguinte PVI de ordem dois
⎧ y ' ' = 3 y '−2 y
⎪
⎨ y (0) = −1
⎪ y ' (0) = 0
⎩
Seja z=y’ então y’’=z’ e z(0)=y’(0)=0. Ou seja obteve-se o seguinte sistema de PVI de
ordem um:
⎧ z ' = 3z − 2 y
⎪ y' = z
⎪
⎨
⎪ y (0) = −1
⎪⎩ z (0) = 0
Um PVI tem solução única se f é uma função real e satisfaz a:
i)
é definida e contínua na faixa a≤x≤b, -∞<y<∞, com a e b finitos;
2
ii)
existe uma constante L tal que para qualquer x pertencente ao intervalo [a, b], e
todo o par de números y e y*
f ( x, y ) − f ( x, y * ) ≤ L y − y * ,
a condição anterior designa-se por condição de Lipschitz.
Se f satisfaz as condições anteriores então existe exactamente uma função y(x) que
satisfaz:
i)
y(x) é contínua e diferenciável em [a,b],
ii)
y’(x)=f(x, y(x)), x∈[a, b],
iii)
y(a)=η, com η um número dado.
2. Solução numérica de um PVI de primeira ordem: Métodos de passo
simples
Suponhamos que o PVI (7.1) satisfaz as condições de existência e unicidade de solução,
vai tentar-se encontrar uma solução numérica para o problema.
Considere-se m subintervalos de [a, b], (m≥1), e seja xj=x0+jh onde h =
b−a
, j=0,...,m e
m
xj∈[a,b]. Ao conjunto Ih={x0,x1,...,xm}obtido da forma anterior chama-se rede ou malha de
[a,b].
A solução numérica ym(x) é a função linear por partes, cujo gráfico é uma poligonal com
vértices nos pontos (xj,yj), onde yj foi calculado usando algum dos métodos numéricos que
serão vistos a seguir.
Se m=2n, então hm =
b−a
2n
, n=0,1,..., e a sucessão de funções poligonais {yn(x)}
converge uniformemente para a solução y(x) do PVI.
O objectivo dos métodos numéricos é o cálculo dos vértices {y0,y1,...,ym}.
3
Notação:
y(xj), j=0,...,m ⎯ solução exacta do PVI nos pontos xj∈Ih
y(xj)≅yj ⎯ significa que yj é aproximação para y(xj), xj∈Ih.
2.1. Métodos da série de Taylor: Método de Euler
Considere-se o PVI
⎧ y ' = f ( x, y )
, η um número dado.
⎨
⎩ y ( x0 ) = y 0 = η
Desejam-se aproximações y1, y2,...,ym para as soluções exactas y(x1), y(x2),..., y(xm).
Comecemos por determinar a aproximação y1 para y(x1).
Seja T a tangente à curva y(x) no ponto (x0, y(x0)), a equação de T é:
y(x)- y(x0)=(x-x0)y’(x0).
Fazendo x=x1 e notando que
y(x0)=y0 ⎯ condição inicial
x1-x0=h
y’(x0)=f(x0,y(x0))
y1≅y(x1)
tem-se que
y(x1)-y(x0)=(x1-x0)y’(x0) ⇔ y1-y0=hf(x0,y(x0)) ⇔ y1=y0+hf(x0,y(x0)).
O erro cometido na aproximação de y(x1) por y1 é: e1=y1-y(x1), ou seja, a diferença entre
a solução numérica e a solução exacta. y2 obtém-se de modo análogo ao de y1, tendo-se
que:
y2=y1+hf(x1,y(x1))
e2=y2-y(x2)
Genericamente,
yj+1=yj+hf(xj,y(xj)), j=0,1,...,m-1
cujo erro é
ej+1=yj+1-y(xj+1), j=0,1,...,m-1
4
O método de Euler consiste, então, em calcular recursivamente a sucessão {yj} através
das fórmulas:
⎧ y0 = y (a) = η
⎨
⎩ y j +1 = y j + hf ( x j , y j ), j = 0,..., m − 1
Interpretação analítica do método de Euler
Expandindo a solução y(x) em série de Taylor em torno do ponto xj,
y ( x j + h) = y ( x j ) + hf ( x j , y ( x j )) +
1 2
1
h y ' ' ( x j ) + ... + h n y ( n) ( x j )
2!
n!
Truncando a série após o termo em h e identificando y(xj) com yj obtém-se a igualdade
pretendida, ou seja, o método de Euler.
Exemplo
Achar aproximações para a solução do PVI
⎧ y' = x − y + 2
⎨
⎩ y ( 0) = 2
na malha [0,1] com h=0.2.
Tem-se que x0=0 e y0=2.
1º iteração y1=y0+hf(x0,y0) ⇔ y1=2+0.2f(0, 2) ⇔ y1=2; x1=0+0.2=0.2
2º iteração y2=y1+hf(x1,y1) ⇔ y2=2+0.2f(0.2, 2) ⇔ y2=2.04; x2=0.2+0.2=0.4
3º iteração y3=y2+hf(x2,y2) ⇔ y3=2.04+0.2f(0.4, 2.04) ⇔ y3=2.112; x3=0.4+0.2=0.6
4º iteração y4=y3+hf(x3,y3) ⇔ y4=2.112+0.2f(0.6, 2.112) ⇔ y4=2.2096; x4=0.6+0.2=0.8
5º iteração y5=y4+hf(x4,y4) ⇔ y5=2.2096+0.2f(0.8, 2.2096) ⇔ y5=2.32768; x5=0.8+0.2=1
As soluções aproximadas na malha [0, 1] são: {2, 2.04, 2.112, 2.2096, 2.32768}.
5
Métodos de Passo Simples
Um método para resolver um PVI é de passo simples se a aproximação yj+1 depende
apenas dos resultados de yj da etapa anterior. Todos os métodos de passo simples são
escritos na forma:
(7.2)
yj+1=yj+hΦ(xj,yj,h ), j=0,1,...,m-1,
onde Φ é a função incremento e h o comprimento do passo. O método de Euler é um
exemplo de um método de passo simples com função incremento Φ(xj,yj,h )=f(xj, yj).
Diz-se que um método da forma (7.2) possui ordem r se r for o maior número inteiro
para o qual
y(x+h)-y(x)-hΦ(x, y(x), h)=o(hr+1),
onde y(x) é a solução teórica do PVI.
O método de Euler é de ordem um.
Métodos com derivadas
O método de Euler ou método de Taylor de 1ª ordem, foi obtido a partir da fórmula de
Taylor, onde se tomaram termos até ao termo em h. Teoricamente, pode-se afirmar que a
fórmula de Taylor fornece tantos métodos quantos se queiram, desde que se calculem as
derivadas necessárias. O método de Taylor de 2ª ordem é,
y j +1 = y j + hy ' ( x j ) +
h
y ' ' ( x j ) , j=0,..,m-1
2!
Os métodos que usam a fórmula de Taylor apresentam alguns inconvenientes
computacionais: deve-se operar simultaneamente com várias funções, i.e., as derivadas da
função f, o que aumenta em muito o espaço ocupado na memória do computador. Além
disso, a complexidade das expressões analíticas para as derivadas de f aumenta com a
ordem de derivação de f, salvo casos triviais. Em geral, estes métodos não são usados.
6
Essa é a razão por que serão obtidos, a seguir, métodos de precisão equivalente aos
métodos da fórmula de Taylor, porém sem o inconveniente de se calcularem derivadas;
são os chamados métodos de Runge-Kutta ⎯ RK.
2.2. Métodos de Runge-Kutta
2.2.1. Métodos de Runge-Kutta de segunda ordem
As fórmulas têm a forma geral
[
⎧ y j +1 = y j + h af ( x j , y j ) + bf ( x j + αh, y j + β hf ( x j , y j ))
⎨
⎩ y 0 = y ( x0 )
]
j=0,...,m-1
sendo as constantes a,b,α e β escolhidas de modo que o erro de truncatura local do método
seja proporcional a h3 tal como o método de Taylor de 2ª ordem.
⎧a = 1 − b
Tal condição implica ⎪⎨
1
⎪⎩α = β = 2b
, sendo b arbitrário.
Apresentaremos aqui os dois métodos mais conhecidos de Runge-Kutta de 2ª ordem.
1
2
1
2
O método de Euler melhorado corresponde à escolha b = ,e tem-se a = , α = β = 1 :
h
⎧
⎪ y j +1 = y j + 2 (k1 + k 2 )
⎪
⎪ y 0 = y ( x0 )
⎪
⎨
⎪k = f ( x , y )
j
j
⎪ 1
⎪k 2 = f ( x j + h, y j + hk1 )
⎪⎩
7
j = 0,..., m - 1
1
2
O método de Euler modificado corresponde à escolha b = 1 ,e tem-se a = 0 , α = β = :
⎧
⎪ y j +1 = y j + hk 2
⎪
⎪ y 0 = y ( x0 )
⎪
⎨
⎪k = f ( x , y )
j
j
⎪ 1
⎪
h
h
⎪k 2 = f ( x j + , y j + k1 )
2
2
⎩
j = 0,..., m - 1
Exemplo:
Achar aproximações para o PVI
⎧ y' = x − y + 2
⎨
⎩ y (0) = 2
na malha [0,1] com h=0.2, usando o método de Euler melhorado.
Tem-se que x0=0 e y0=2.
h
2
1º iteração: y1 = y 0 + (k1 + k 2 ) . Tem-se que k1= f(x0, y0)=f(0,2)=0
k2=f(x0+h, y0+hk1) ⇔ k2=f(0.2, 2+0.2*0) ⇔ k2=0.2
Donde y1=2+0.1(0+0.2)=2.02; x1=0+0.2=0.2
h
2
2º iteração: y 2 = y1 + (k1 + k 2 ) . Tem-se que k1= f(x1, y1)=f(0.2,2.02)=0.18
k2=f(x1+h, y1+h k1) ⇔k2=f(0.4, 2.02+0.2*0.18) ⇔ k2=0.344
Donde y2=2.02+0.1(0.18+0.344)=2.0724; x2=0.2+0.2=0.4
h
2
3º iteração: y3 = y 2 + (k1 + k 2 ) . Tem-se que k1= f(x2, y2)=f(0.4,2.0724)=0.3276
k2=f(x2+h, y2+h k1)⇔ k2=f(0.6, 2.0724+0.2*0.3276) ⇔ k2=0.46208
Donde y3=2.0724+0.1(0.3276+0.46208)=2.151368; x3=0.4+0.2=0.6
8
h
2
4º iteração: y 4 = y3 + (k1 + k 2 ) . Tem-se que k1= f(x3, y3)=f(0.6, 2.151368)=0.448632
k2=f(x3+h, y3+h k1)⇔k2=f(0.8, 2.151368+0.2*0.448632) ⇔k2=0.5589056
Donde y4=2.151368+0.1(0.448632+0.5589056)=2.25212176; x4=0.6+0.2=0.8
h
2
5º iteração: y5 = y 4 + (k1 + k 2 ) . Tem-se que k1= f(x4, y4)=f(0.8, 2.25212176)=0.54787824
k2=f(x4+h,y4+h k1)⇔k2=f(1, 2.25212176+0.2*0.54787824)⇔k2=0.638302592
Donde y5=2.25212176+0.1(0.54787824+0.638302592)=2.370739843; x5=0.8+0.2=1
9