Aula 09

Solução de Equações Diferenciais Ordinárias (EDO):

x t   f x, t 
 xto  xo
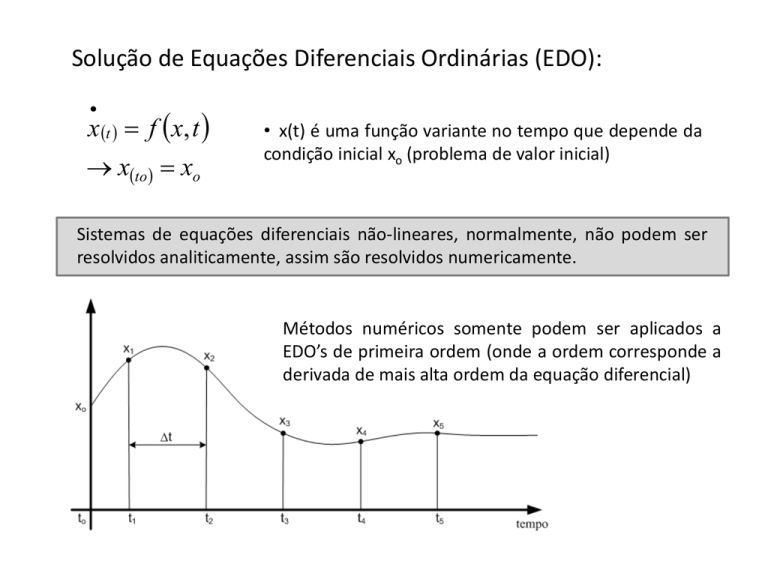
• x(t) é uma função variante no tempo que depende da
condição inicial xo (problema de valor inicial)
Sistemas de equações diferenciais não-lineares, normalmente, não podem ser
resolvidos analiticamente, assim são resolvidos numericamente.
Métodos numéricos somente podem ser aplicados a
EDO’s de primeira ordem (onde a ordem corresponde a
derivada de mais alta ordem da equação diferencial)
Métodos baseados na Série de Taylor:

x t   f x, t 
1 
1  p
2
p
x tn1   x tn   x tn   tn 1  tn    x tn   tn1  tn      x tn   tn1  tn   t.a.o.
2
p!



t n1  t n  h
h 2 
h p  p
x tn1   x tn   h  x tn    x tn      x tn   t.a.o.
2
p!



h 2 
h p  p
x tn1   x tn   h  x tn    x tn      x tn   t.a.o.
2
p!





x t   f  x , t   x t n   f  x  t n  , t 



0


h

 h



x tn1   t.a.o  x tn   h  f  x tn  , t    f  x tn  , t      f
p!

 2




2
p
p 1


 x tn  , t 



x tn1   xn 1


x  t n   xn
h2
hp
xn1  xn  h  f xn , t    f xn , t      f
2
p!
p 1
xn , t 
xn1  xn  h  Tpxn 
h
h p 1
Tp( xn )  f xn , t    f xn , t    
f
2
p!
p 1
xn , t 
• “p” indica a ordem do método de integração
A aplicação direta da Série de Taylor possui pouca precisão quando a ordem é
baixa e grande complexidade e esforço computacional quando a ordem é
elevada, por estas razões não é utilizada na prática.
Série de Taylor para p=1:
xn1  xn  h  f xn , tn 
Método de Euler
Série de Taylor para p=2:
h2
xn 1  xn  h  f xn , tn    f xn , tn 
2
h2
xn1  xn  h  f xn , tn     f xxn , tn   f txn , tn 
2
Se a ordem da Série de Taylor aumenta também aumenta o número de
derivadas e derivadas parciais, dificultando assim o uso de derivadas analíticas.
A substituição de derivadas por aproximações deu origem aos métodos de
Runge-Kutta.
Método de Runge-Kutta de 4ª ordem:
xn1  xn  h  K 4 xn , tn 
1
K 4  T4  K 4   k1  2  k 2  2  k3  k 4 
6
• Ki representam aproximações
da função para “i’s” diferentes
pontos entre tn e tn+1
k1  f xn , t n 
h
h

k 2  f  xn   k1 , t n  
2
2

h
h

k 3  f  xn   k 2 , t n  
2
2

k 4  f  xn  h  k 3 , t n  h 
Método derivados da Série de Taylor
Estabilidade fraca
 são métodos de passo único, nenhuma informação de pontos anteriores a tn são
requeridos
 são métodos explícitos, somente dependem da informação de tn para calcular tn+1.
Métodos explícitos a presentam o problema de propagação do erro de truncamento,
o que compromete a sua estabilidade numérica, para reduzir isso pequenos passos
de integração “h” devem ser utilizados
 são de fácil implementação
Método Multipasso: usam informação de mais de um ponto para calcular
x(tn+1)

x  t   f  x, t  
t n1
t n1
 x  dt   f x  , t  dt

t
tn
xtn1   xtn  
t
tn
t n1
 f x  , t  dt
t
tn
t n1
aproximação por um polinômio de grau “k”
 p t  dt
k
tn
Uma função pode ser aproximada por um polinômio de grau adequado em um
intervalo finito tn
tn+1. Assim, xn+1 pode ser calculado como uma função
polinomial de estimativas prévias xn, xn-1,... e funções f(xn,tn), f (xn-1,tn-1), ...
Método Explícitos (Adams-Bashford): obtem Xn+1 a partir de xn, xn-1,
xn-2, ... Xn-k
 São métodos explícitos, e como tal
o erro de truncamento é cumulativo;
 São métodos não auto-iniciáveis.
Oh1   xn 1  xn  h  f xn , t n 
Método de Euler
h
Oh 2   xn 1  xn   3  f xn , t n   f xn 1 , t n 1 
2
h
Oh3   xn 1  xn   23  f xn , t n   16  f xn 1 , t n 1   5  f xn  2 , t n 2 
12
Método Implícitos (Adams-Moulton): obtem xn+1 a partir de xn+1, xn,
xn-1, xn-2, ... xn-k+1
 Os
métodos
implícitos
não
acumulam erro de truncamento,
porém podem apresentar oscilações
numéricas se um passo de integração
adequado não for utilizado;
 São resolvidos iterativamente.
Oh1   xn 1  xn  h  f xn 1 , t n 1 
Método de Euler Reverso
h
Método Trapezoidal
Oh 2   xn 1  xn    f xn 1 , t n 1   f xn , t n 
2
h
Oh3   xn 1  xn   5  f xn 1 , t n 1   8  f xn , t n   f xn 1 , t n 1 
12
Método de Previsão-Correção:
utilizam um par de fórmulas,
normalmente o previsor é um método explícito de baixa ordem e o corretor um
método implícito de ordem mais elevada.
Algoritmo:
1. calcular x(o)n+1 por um método explícito
2. K=1
3. calcular f (xn+1,tn+1)
4. calcular x(k)n+1 usando um método implícito
5. se | x(k)n+1 - x(k-1)n+1 | / x(k-1)n+1 >
incrementar k e voltar ao passo 3;
senão calcular o próximo passo de integração