UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE

UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE
PROGRAMA INSTITUCIONAL DE BOLSAS DE INICIAÇÃO À DOCÊNCIA
SUBPROGRAMA PIBID/FÍSICA
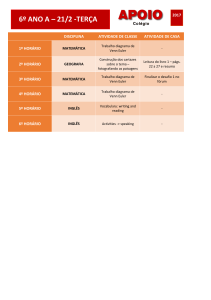
MOSTRA DE EQUAÇÕES
EQUAÇÃO DE EULER
EMANUEL PEREIRA DE ARAÚJO; MACIEL DO NASCIMENTO GOMES;
Com sua enorme facilidade com os cálculos, Euler pode
A Equação de Euler, cujo nome é uma homenagem a
arrumar essas funções trigonométricas de modo que sua
Leonhard Euler, é uma equação específica da análise
soma resultasse em algo idêntico à função exponencial
complexa, que mostra uma relação entre as funções
de base e. Tomando a ajuda do número imaginário
,
trigonométricas e a função exponencial.
ele escreveu:
Em 1740, Euler mostrava que ao escolher a base para
uma função exponencial, havia inúmeras vantagens
matemáticas em selecionar um número criado pela
adição dos termos da série infinita:
Euler percebeu que a soma desses termos é um
número
irracional
2,718281828459...,
então
representou este número por e, assim ele notou que e
pode ser usado como base dos expoentes e a função
pode ser calculada:
Então ele verificou que se x = π e, desde que o seno
de π é 0, e o cosseno é -1, obtinha:
Então reunindo conceitos fundamentais da matemática:
Então descrevendo as propriedades das funções
trigonométricas, Euler observou que as funções de
seno e cosseno poderiam ser expressas em termos de
séries infinitas:
sen x =
cos x =
Euler então usou essas funções para mostrar que
outras funções podem ser expressas como séries
infinitas.
.
Leonhard Euler (1707-1783) foi um matématico e físico
Suíço pioneiro.
REFERÊNCIAS BIBLIOGRÁFICAS: Crease, Robert P. As grandes equações. Rio de Janeiro: Zahar, 2011.
Aaboe, A. Episódios da história da Matemática. Rio de Janeiro: Sociedade Brasileira de Matemática, 1984.
Orientador: Prof. Ciclamio L. Barreto – Depto. de física/UFRN