Caderno de Problemas 688KB Jan 12 2015 03:18:33 PM

CADERNO DE PROBLEMAS DA DISCIPLINA DE
ELECTROMAGNETISMO
ANO LECTIVO DE 2006/2007
Paulo Araújo Sá e Carlos Daniel Pintassilgo
Faculdade de Engenharia da Universidade do Porto (FEUP)
MATEMÁTICA : INTEGRAIS E VECTORES
1. a) Determine a área da superfície de um disco plano de raio R e espessura
desprezável.
b) Suponha que o disco está carregado com uma densidade superficial de carga σ = k1
(k1 = constante). Determine a carga do disco.
c) Suponha agora que o disco está carregado com uma densidade superficial de carga
σ = k (R − r ) , onde k é uma constante e r representa a habitual coordenada polar.
Determine a carga do disco.
2. Considere uma esfera de raio R electrizada em superfície com uma densidade σ.
Calcule a carga total da esfera, definida pela expressão
q = ∫∫ σ (P )dS
S
nos seguintes casos :
a) σ (P) = C1 = constante;
b) σ (P ) = c2ϕ cos 2 θ , onde c2 é uma constante e θ e φ representam as coordenadas
esféricas usuais.
3. Considere uma esfera de raio R electrizada em volume com uma densidade ρ. Calcule
a carga total da esfera, definida pela expressão
q =
∫∫∫ ρ (P )dV
V
nos seguintes casos :
a) ρ (P) = k1 = constante;
b) ρ (P ) = k 2 rϕ cos 2 θ , onde k2 é uma constante e r, θ e φ as habituais coordenadas
esféricas.
4. Considere um cone sólido de altura h igual ao raio da base R, electrizado em volume
com uma densidade de carga ρ. Calcule a carga do cone nas duas situações seguintes:
a) ρ (P) = k1 = constante;
b) ρ (P) = kr, onde k é uma constante e r a distância de um ponto do cone ao eixo dos
zz. Quais são as dimensões de k ? No Sistema Internacional de Unidades (SI), em que
unidades expressaria k ?
5. Obtenha o versor normal à superfície x 2 + xy + 4 z = 8 , no ponto (2,0,1).
r
r
6. Dados os dois vectores rA = −iˆ − 3 ˆj − 4kˆ e rB = 2iˆ + 2 ˆj + 2kˆ e o ponto C ≡ (1; 3; 4),
determine :
r
r r
a) RAB = rB − rA ;
r
b) rA ;
c) r̂A ;
d) R̂ AB ;
e) o versor da direcção C A , apontando do ponto C para o ponto A;
r
r
f) o ângulo entre RAB e RAC ;
r
r
g) o vector projecção de RAB em RAC ;
r
r
h) RBC ∧ RBA ;
i) um vector unitário normal ao plano definido pelos três pontos A, B e C.
7. a) Escreva em coordenadas cartesianas o vector com origem no ponto P
( r = 4; ϕ = 10º ; z = 1 ) e extremidade no ponto Q ( r = 7; ϕ = 75º ; z = 4 ).
b) Escreva em coordenadas cilíndricas no ponto especificado cada um dos três seguintes
vectores :
r
i) v1 = 5iˆ em P( r = 4; ϕ = 120º ; z = 2 );
r
ii) v2 = 5iˆ em Q(x = 3; y = 4; z = -1);
r
iii) v3 = 4iˆ − 2 ˆj − 4kˆ em R(x = 2, y = 3; z = 5);
c) Qual é o afastamento do ponto A(110; 60º; -20) relativamente ao ponto B(30; 125º;
10) ?
8. Dados os pontos A(x = 2; y = 3; z = -1) e B( r = 4;θ = 25º ; ϕ = 120º ), determine :
a) as coordenadas esféricas do ponto A;
b) as coordenadas cartesianas do ponto B;
c) a distância entre A e B.
9. Transforme cada um dos seguintes vectores para coordenadas esféricas no ponto
especificado:
r
a) w1 = 5iˆ em A( r = 4;θ = 25º ; ϕ = 120º );
r
b) w2 = 5iˆ em B(x = 2; y = 3; z = -1);
r
c) w3 = 4iˆ − 2 ˆj − 4kˆ em C(x = 2; y = -3; z = 4).
ELECTROSTÁTICA : CAMPO E POTENCIAL ELÉCTRICO
1. a) Um electrão (carga e = − 1,6 × 10 −19 C ) está colocado no ponto (1m; 2m; 0) e uma
partícula α (carga qα = + 2 e ) está situada no ponto (2m; 1m; 0). Determine a força que
a partícula α exerce sobre o electrão.
b) Considere agora que ao sistema das duas cargas anteriores se vem juntar uma terceira
carga de valor q = −4,8 × 10 −19 C que é colocada no ponto (3m; 2m; 0). Determine a
força total que actua sobre o electrão.
2. Duas partículas de massa m e carga q estão suspensas do mesmo ponto por dois fios
de comprimento l. Mostre que em equilíbrio a inclinação θ de cada fio relativamente à
vertical é dada por:
16πε 0 mgl 2 sen 3θ = q 2 cosθ .
3. Uma carga de 2,5 × 10-8 C está num campo eléctrico uniforme, orientado
verticalmente de baixo para cima e com intensidade 5 × 104 NC-1. Calcule o trabalho
realizado pelo campo eléctrico sobre a carga quando esta se move :
a) 45 cm para baixo;
b) 75 cm para a direita;
c) 2,10 m acima da horizontal segundo um ângulo de 450.
4. Um electrão é lançado numa região onde há um campo eléctrico uniforme, com uma
intensidade de 5 ×103 NC-1, dirigido para cima. A velocidade inicial do electrão é de 107
ms-1, fazendo um ângulo de 30º com a horizontal.
a) Calcule :
i) o tempo necessário para o electrão alcançar a sua altura máxima;
ii) a distância máxima atingida pelo electrão, segundo a vertical, acima da sua posição
inicial;
iii) a distância horizontal percorrida pelo electrão até regressar à altura inicial;
b) Faça um esboço da trajectória do electrão.
5. Um fio de comprimento L possui uma densidade linear de carga λ, uniforme.
a) Determine a força que o fio exerce sobre uma carga Q que se encontra sobre a sua
linha de acção e a uma distância h da extremidade do fio que lhe é mais próxima.
b) Determine a força que o fio exerce sobre uma carga Q situada a uma distância a do
fio e na perpendicular ao meio do fio. Comente o comportamento da força quando L →
0 e quando L → ∞, mantendo em ambos os casos a constante.
c) Determine o módulo e a direcção da força que o fio exerce sobre uma carga Q situada
verticalmente sobre uma das extremidades do fio e a uma distância H dessa
extremidade.
6. Considere um disco de raio R carregado com uma distribuição superficial de carga σ,
uniforme. Determine a força que o disco exerce sobre uma carga Q situada a uma
distância a, na vertical do disco e sobre o seu eixo.
7. Considere a configuração discreta de cargas mostrada na figura.
z
P
(0,0,z)
q
(0,-a,0)
x q
(a,0,0)
q
(-a,0,0)
q
y
(0,a,0)
Determine :
a) o campo eléctrico no ponto P;
b) o potencial eléctrico no mesmo ponto.
8. Três cargas positivas, de 2 × 10-7 C, 10-7 C e 3 × 10-7 C, estão alinhadas segundo uma
dada direcção, com a segunda carga no centro da configuração. A distância entre cargas
adjacentes é de 10 cm. Calcule :
a) a força resultante exercida sobre cada carga, devida às outras duas;
b) a energia potencial de cada carga devida à presença das outras;
c) a energia interna do sistema, comparando-a com a soma das energias potenciais.
Explique a existência de alguma diferença.
9. Dois fios semi-infinitos estão colocados sobre a mesma linha de acção, distando os
seus topos de uma distância a, tal como está esquematizado na figura abaixo. Cada um
dos fios está carregado com uma distribuição linear de carga uniforme λ.
Determine o vector campo eléctrico criado por esta distribuição de carga no ponto P,
situado a uma distância d do meio do segmento não carregado AB .
P
d
B
A
a
10. Uma carga de valor Q1 encontra-se uniformemente distribuída ao longo de uma
semi-circunferência de raio R e duas cargas pontuais, ambas com o valor Q2, estão
colocadas ao longo do eixo dos xx nos pontos indicados na figura. O sistema está no
vácuo. Em função da carga Q1, que valor deverá ter Q2 para que:
a) o potencial V no ponto O seja nulo.
r
b) o vector campo eléctrico E seja nulo no ponto O.
Q1
Q2
Q2
R
O
R
R
11. Considere um aro de raio a carregado com uma densidade linear de carga λ,
uniforme.
a) Determine, num ponto genérico do eixo do aro, o campo eléctrico e o potencial
eléctrico:
r
i) começando por determinar E e, em seguida, calculando V a partir do
r
resultado de E ;
r
ii) começando por calcular V e, depois, determinando E à custa do resultado
de V.
(*)b) Estime a distância máxima para a qual o aro pode ser considerado uma carga pontual
r
se o erro máximo admissível para E for de 1%.
12. Um disco, situado no plano z = 0, encontra-se carregado com uma densidade
superficial de carga σ, uniforme. O disco tem raio R.
a) Determine o campo eléctrico num ponto P genérico do eixo do disco:
i) a partir das contribuições elementares;
ii) utilizando o resultado obtido no problema anterior para o campo eléctrico
criado pelo aro.
r
(*)b) Que resultado obtém para E no limite R → ∞ ? Verifique também o que acontece
quando z >> R. Estime, neste caso, a distância mínima para a qual o disco pode ser
r
considerado uma carga pontual, sabendo que o erro máximo admissível para E é de
1%.
(*)c) Calcule o potencial electrostático no mesmo ponto P e estime a distância ao disco
para a qual este pode ser considerado uma carga pontual se o erro máximo admissível
para V for de 1%.
13. Entre duas placas paralelas de cargas opostas há um campo eléctrico uniforme. Um
electrão é libertado do repouso da superfície da placa carregada negativamente e vai
atingir a superfície da outra placa, situada a 2 cm da primeira, num intervalo de tempo
de 1,5 × 10-8 s.
a) calcule a intensidade do campo eléctrico.
b) Determine a velocidade do electrão ao atingir a segunda placa.
c) Qual é a diferença de potencial entre as duas placas ?
ELECTROSTÁTICA : LEI DE GAUSS E ELECTROSTÁTICA DOS
CONDUTORES
1. Considere uma esfera de raio R, carregada com uma densidade volumétrica de carga
ρ, uniforme.
a
O
R
P
Determine:
(*) a) o campo eléctrico no ponto P, exterior à esfera e distando a do seu centro. Utilize,
para o efeito, o resultado obtido para o campo criado por um disco num ponto situado
sobre o eixo normal ao disco e que passa no seu centro.
b) o campo eléctrico num ponto genérico interior à esfera, recorrendo à lei de Gauss.
c) o fluxo do campo eléctrico estendido a uma superfície esférica, concêntrica com a
esfera carregada, que contenha o ponto P da alínea a).
2. Considere uma esfera de raio R carregada com uma densidade volumétrica de carga
ρ = Qr (πR 4 ) , onde Q é uma constante.
a) Verifique que Q é a carga total da esfera.
b) Determine o campo eléctrico dentro, sobre e fora da esfera.
c) Calcule o potencial eléctrico nos mesmos pontos da alínea anterior.
3. Uma esfera não condutora de raio R1, possui uma cavidade central concêntrica de raio
R2, e está carregada com uma carga q distribuída uniformemente sobre o seu volume.
a) Determine o campo e o potencial eléctrico:
i) fora da esfera;
ii) dentro da massa da esfera;
iii) na cavidade.
b) Esboce graficamente o campo e o potencial eléctrico como função da distância r ao
centro da esfera.
(*) 4. Uma esfera, representada em corte na figura, possui uma cavidade também esférica.
Suponha que a esfera, excepto na cavidade, se encontra carregada com uma densidade
volumétrica de carga ρ, uniforme.
R
a
RC
Determine o vector campo eléctrico:
a) no interior da cavidade;
b) na massa da esfera;
c) no exterior da esfera.
5. A figura representa um fio rectilíneo, infinito, uniformemente electrizado com uma
densidade linear de carga λ, e uma esfera de raio R, uniformemente electrizada em
superfície com uma densidade superficial σ.
a) Determine o vector campo eléctrico na origem, O, do referencial.
b) Determine a diferença de potencial entre a origem O e o ponto P (0; d) representado
na figura.
c) Calcule o trabalho realizado pelo campo eléctrico no transporte de uma carga pontual
q da origem O até ao ponto P.
y
P(0;d)
-d
d
O
λ
R
σ
x
6. Duas superfícies planas paralelas e condutoras encontram-se aos potenciais 0 e V0
(ver figura). Determine o potencial eléctrico e o campo eléctrico entre os planos,
sabendo que a distância entre eles é d.
V0
d
7. Duas superfícies cilíndricas condutoras, de raios R1 e R2 (com R2 > R1), encontram-se
ao potencial zero. Se entre essas superfícies existir uma distribuição volumétrica de
carga ρ uniforme, determine o potencial eléctrico nessa região.
ρ
R1
R2
∞
∞
8. Suponha que o vector campo eléctrico num certo ponto se pode escrever como
r
E = kr 3uˆr , quando escrito em coordenadas esféricas, sendo k uma constante. Determine:
a) a densidade de carga ρ criadora do campo;
b) utilizando dois processos diferentes, a carga total contida numa esfera de raio R
centrada na origem.
9. Duas esferas condutoras com raios 10-3 m e 1,5 × 10-3 m e com cargas de 10-7 C e 2 ×
10-7 C, respectivamente, são postas em contacto eléctrico e, em seguida, separadas.
Calcule a carga eléctrica final em cada esfera.
10. Uma esfera condutora, de raio R1, tem uma cavidade central concêntrica, de raio R2.
No centro da cavidade há uma carga Q.
a) Determine a carga sobre as superfícies interna e externa do condutor.
b) Calcule o campo e o potencial eléctrico fora da esfera, dentro dela e na cavidade.
c) Represente graficamente o campo e o potencial eléctrico como função da distância ao
centro.
11. Uma esfera metálica de raio R, carregada com uma carga Q, está rodeada por uma
casca metálica, de raio interior a e raio exterior b , que não está carregada.
b
a
R
a) Determine a densidade superficial de carga, σ, nas superfícies de raios R, a e b.
b) Calcule o potencial eléctrico no centro da esfera, utilizando o infinito como
referência.
c) Suponha que a superfície exterior da casca é ligada à terra por um fio condutor, o que
origina que o seu potencial fique a zero (o mesmo que no infinito). Como é que se
alteram as suas respostas às alíneas a) e b) ?
MATEMÁTICA : ANÁLISE VECTORIAL
r
1
1. Considere o campo vectorial E = 2 x 2 yiˆ + y 2 zˆj + x 5 y 2 kˆ .
r r r
a) Calcule a divE = ∇ ⋅ E .
r
b) Obtenha a divE no ponto (1; 1; 1).
r r r
c) Determine o rotE = ∇ × E e calcule o seu valor no ponto (1; 1; 1).
2. Considere o campo vectorial definido em coordenadas esféricas pela expressão:
r
E = ruˆ r + senϕuˆϕ .
r
a) Calcule, utilizando coordenadas esféricas, a divE .
r
b) Obtenha a divE em coordenadas cartesianas, transformando o resultado obtido na
alínea anterior.
r
c) Determine novamente a divE em coordenadas cartesianas começando, agora, por
r
r
exprimir E nessas coordenadas e aplicando seguidamente o operador ∇ .
3. Seja S1 uma superfície quadrada de lado a situada no plano z = 0 . Considere o
r
campo vectorial de intensidade constante V = 2iˆ − 3 ˆj − 4kˆ. Calcule o fluxo de
r
V através da superfície S1, admitindo que a normal à superfície é positiva no sentido
positivo do eixo dos zz.
r
r
4. Considere o campo vectorial V = xiˆ + yˆj + zkˆ . Determine o fluxo de V ,
r r
∫ V ⋅dS ,
S
se S for :
a) a superfície de uma esfera de raio b centrada na origem e com normal a apontar para
o exterior;
b) a superfície definida por z = c, -d < x < d, -d < y < d e com normal segundo o sentido
positivo do eixo dos zz.
5. Verifique o teorema da divergência utilizando a função vectorial
r
v = y 2iˆ + 2 xy + z 2 ˆj + 2 yzkˆ e o cubo de aresta unitária representado na figura.
(
)
z
y
x
6. a) Determine o fluxo, estendido a 1/8 da superfície de uma esfera, tal como
representado na figura, de um campo vectorial definido por :
r
E = r 2uˆr + rsenθuˆθ + ruˆϕ .
z
1
1
1
y
x
b) Confirme o resultado recorrendo ao teorema da divergência.
r
r
7. O campo vectorial V de intensidade constante é definido por V = V0 iˆ , onde V0 é
uma constante. Determine o integral de caminho
r
r
I = ∫ V ⋅ dl ,
P
onde P é :
a) o percurso fechado representado na figura 1;
b) o percurso cm a forma de uma semicircunferência de raio a centrada na origem no
plano xy, tal como mostrado na figura 2.
y
y
(x0,y0)
(0,y0)
a
(0,0)
(x0,0)
x
x
Figura 2
Figura 1
r
8. Considere a função vectorial F = 2 x + y 2 iˆ − 3 yzˆj + kˆ .
(
)
a) Determine o valor do integral de linha:
b
r r
F
∫ ⋅ dr
a ( C1 )
quando a ≡ (0; 0; 0), b ≡ (1; 1; 1) e C1 é o percurso (0; 0; 0) - (1; 0; 0) - (1; 1; 0) - (1; 1;
1).
b) Calcule o valor do integral de linha mas supondo que agora o percurso é C2, o
segmento de recta que une a origem ao ponto (1; 1; 1).
9. Suponha o seguinte campo vectorial:
r
v = (2 xz + 3 y 2 ) ˆj + 4 yz 2 kˆ .
z
(0,0,1)
Verifique o teorema de Stokes para a superfície
quadrada esquematizada na figura ao lado.
(0,1,0) y
x
ELECTROSTÁTICA : CONDUTORES, DIELÉCTRICOS E
CONDENSADORES
1. A intensidade do campo eléctrico na superfície de um condutor é 104 V cm-1.
a) Qual é a densidade superficial de carga no condutor ?
b) Qual é a área média da superfície que tem à sua disposição uma carga eléctrica igual
à de um electrão ?
2. Dois condutores planos paralelos estão separados por uma distância d. Uma folha
plana carregada com uma densidade superficial de carga σ está situada entre as placas e
paralelamente a estas, a uma distância x de uma delas. Calcule a carga eléctrica
induzida em cada placa.
3. Um dipolo eléctrico é constituído por duas cargas eléctricas com o mesmo valor mas
de sinais contrários, separadas por uma distância d.
a) Obtenha a expressão do potencial eléctrico criado por um dipolo no ponto P (x; y; z)
situado a uma distância muito grande quando comparada com a separação d entre as
duas cargas.
b) Determine o vector campo eléctrico nesse ponto.
c) Mostre que se se aplicar sobre um dipolo eléctrico um campo eléctrico exterior este
tende a orientar o dipolo segundo a direcção do campo.
4. A permitividade eléctrica do diamante é de 1,46 × 10-10 C2 m-2 N-1.
a) Qual é a constante dieléctrica do diamante ?
b) Qual é a susceptibilidade eléctrica do diamante ?
5. Considere a configuração esférica, esquematizada na seguinte figura, constituída por
camadas esféricas concêntricas de materiais dieléctricos limitadas por uma casca
condutora. Nas regiões 1, 3 e 5 há vácuo, a região 2 está preenchida por um dieléctrico
de permitividade relativa k e a região 4 é um condutor metálico.
c
d
3
2
b
1
a
ε0
ε2=kε0
4 (condutor)
Se no centro desta configuração for colocada uma carga Q, determine:
r
a) o vector deslocamento eléctrico D nas várias regiões indicadas;
r
b) o vector campo eléctrico E nessas regiões;
r
c) o vector polarização eléctrica P nessas regiões;
d) a densidade superficial de carga nas superfícies condutoras;
e) a densidade superficial de carga de polarização nas superfícies dieléctricas;
f) a densidade volumétrica de carga de polarização no interior do material dieléctrico.
6. Num meio dieléctrico com εr = 4, o vector campo eléctrico escreve-se:
r
E = ( x 2 + 2 z )iˆ + x 2 ˆj − ( y + z )kˆ
(Vm-1)
Calcule a energia electrostática armazenada na região − 1 ≤ x ≤ 1m , 0 ≤ y ≤ 2m e
0 ≤ z ≤ 3m .
7. Um condensador de ar, formado por duas placas paralelas que estão muito próximas
uma da outra tem uma capacidade de 1000 pF. A carga em cada placa é de 1µC.
a) Calcule a diferença de potencial e o campo eléctrico entre as placas.
b) Supondo que a carga se mantém constante, calcule a diferença de potencial e o
campo eléctrico entre as placas se a sua separação duplicar.
c) Calcule o trabalho que é necessário realizar para duplicar a distância entre as placas.
8. Pode-se obter um condensador colocando uma folha de papel de 4 × 10-5 m de
espessura entre duas lâminas finas de folha-de-flandres. O papel tem uma constante
dieléctrica relativa de 2,80 e conduz electricidade se estiver submetido a um campo
eléctrico com uma intensidade igual ou superior a 5,00 × 107 V m-1 (isto é, a rigidez
dieléctrica do papel é de 50,0 MV m-1).
a) Determine a área da placa necessária para ter um condensador de papel e de folha-de-
flandres com uma capacidade de 0,3 µF.
b) Calcule a diferença de potencial eléctrica máxima que pode ser aplicada, se o campo
eléctrico do papel não puder exceder metade da rigidez dieléctrica.
9. Determine a capacidade de um cabo coaxial formado por dois condutores cilíndricos
coaxiais de comprimento L e raios a e b (com a < b << L). Suponha que os condutores
têm uma densidade superficial de carga uniforme e que entre eles há um dieléctrico de
permitividade eléctrica ε.
ε
b
condutor a
aa
condutor b
L
10. Três condutores cilíndricos concêntricos têm raios 1 cm, 2 cm e 3 cm. O espaço
entre eles está preenchido com um óleo de permitividade relativa εr = 2,2. Se a máxima
intensidade do campo eléctrico que o óleo pode suportar sem disrupção for de 5 × 106 V
m-1, estime o valor :
a) da maior diferença de potencial que pode ser estabelecida entre os condutores interior
e exterior;
b) da tensão entre os condutores interior e do meio nas condições da alínea anterior.
11. a) Determine a capacidade de um condensador esférico formado por duas cascas
esféricas condutoras concêntricas de raios a e b (a < b). Mostre que se a esfera exterior
for muito grande, obtém a capacidade de um condutor esférico isolado : C = 4πεa.
b) Suponha agora que na região entre as duas cascas esféricas, isto é, a < r < b, há uma
camada esférica de material dieléctrico (de permitividade eléctrica ε) de raio interior a e
exterior c, e que há o vácuo para c < r < b – ver figura. Determine a capacidade deste
condensador.
b
c
ε0
a
ε
12. Considere um condensador formado por duas placas paralelas de área S e separadas
por uma distância d. Admita que d é pequeno quando comparado com as dimensões
lineares da placa. Tal como mostrado na figura, entre as placas e paralelamente a elas há
duas camadas de materiais dieléctricos de permitividades ε1 e ε2 e com espessuras d1 e
d2, respectivamente.
Determine a capacidade deste condensador.
Área S
ε2
d2
d
ε1
condutor 1
d1
condutor 2
13. Um condensador de placas paralelas tem as suas placas colocadas nos planos x = 0 e
x = d e o espaço entre elas está preenchido com um material dieléctrico não homogéneo
de permitividade ε = 2dε 0 ( x + d ) . Se a placa situada em x = d estiver ao potencial V0 e
a placa em x = 0 estiver ligada à terra, determine:
r
a) o vector campo eléctrico, E ;
r
b) o vector polarização, P ;
c) a densidade superficial de carga de polarização, σp, em x = 0 e x = d;
d) a capacidade do condensador quando d = 2,5 mm e a área de cada placa é de 200
cm2.
LEI DE LORENTZ
1. Um fio condutor rectilíneo percorrido por uma corrente eacionário de 6 A, está num
campo magnético uniforme de 0,4 T. Qual é o módulo da força exercida pelo campo
sobre o fio quando a direcção do fio:
a) é perpendicular ao campo;
b) faz um angulo de 30° com o campo.
2. Um protão e um deuterão são ambos acelerados através de uma diferença de
potencial entrando num campo magnético com a mesma direcção. Sabendo que o
deuterão tem a mesma carga do electrão, enquanto que a sua massa é aproximadamente
o dobro da do protão, indique qual será o raio da trajectória do deuterão ee o protão
seguir uma trajectória circular de raio Rp?
r
3. Um electrão entra com velocidade v 0 numa região do espaço onde existe um campo
r
r
magnético uniforme B , cuja direcção é perpendicular a v 0 – ver figura.
r
B
e
ALVO
-
r
v0
-
VA
+
L
a) Estude a trajectória do electrão;
b) Supondo que o electrão sofre apenas um pequeno desvio relativamente à direcção
inicial, obtenha a expressão que descreve a deflexão do electrão num alvo situado a uma
distancia L do ponto de entrada;
r
c) Sabendo que o electrão, antes de entrar na zona do campo B , foi acelerado pelo
campo eléctrico existente entre duas placas paralelas sujeitas a uma diferença de
potencial Va, qual é o valor da velocidade inicial do electrão?;
d) Um tubo de televisão está colocado de modo a que os electrões viajam na direcção
sul-norte. A componente vertical do campo magnético terrestre, dirigida para baixo é
B=5,5x10-5 T. Se o potencial acelerador for de 12 KV, qual será a deflexão do feixe de
electrões ao fim de 20 cm? Que efeito tem a componente horizontal do campo
magnético terrestre?
4. Um electrão animado de velocidade v0 entra numa região do espaço onde existe um
r
r
campo eléctrico E e um campo de indução magnética B .
a) Mostre que no caso mais geral as componentes cartesianas da aceleração do electrão
são:
&x& = −
e
( E x + y& B z − z&B y )
m
&y& = −
e
( E y + z&B x − x&B z )
m
e
( E z + x&B y − y& B x )
m
r
r
)
)
que E =E j e B =B k .
&z& = −
b) Suponha agora
r
r
No instante t=0, r0 =(0,0,0) e v 0 = (v x 0 , v y 0 , v z 0 ) .
Determine as equações paramétricas do movimento do electrão.
(Nota: considere eB/m=ωc).
c) Mostre que no plano XY, o movimento do electrão é uma circunferência de raio
2

E
1 
2
R=
 v xo −  + v y 0 
B
ω c 

1/ 2
,
com centro em
xc = −
v y0
ωc
+
E
t
B
e
yc =
1
ωc
(v x 0 −
E
).
B
d) No caso estudado nas duas alíneas anteriores, o electrão tem um movimento de
deriva segundo x, com uma velocidade vD=E/B. Mostre que se vx0=vD e vy0=0, o
electrão não é deflectido no eixo dos xx;
r
e) Mostre que se existir apenas um campo magnético ( E =0), o centro da circunferência
é estável e tem raio R=vp/ωc =mvp/eB, onde mvp é a componente da quantidade de
r
movimento do electrão perpendicular a B , tendo-se vp=(vxo2+vyo2)1/2, enquanto que ωc é
a frequência ciclotrónica do movimento circular num campo magnético constante.
MAGNETOSTÁTICA: LEI DE AMPÈRE
1.Calcule o módulo do campo B num ponto situado a 5cm de um fio rectilínio de
comprimento infinito quendo este á percorrido por uma corrente estacionária igial a 15
A.
2.No modelo de Bohr para o átomo de hidrogénio, o electrão desloca-se com uma
velocidade de cerca de 2,2x106 m/s numa trajectória circular (r=5,3x10-11 m) em torno
do núcleo.
a) Mostre que nestas condições, o movimento do electrão é equivalente a uma espira
circular percorrida por uma corrente igual a 1,06 mA
b)Determine o valor do módulo de B devido ao movimento do electrão.
3. Uma bobina é formada por 40 espiras circulares de 32 cm de comprimento.
Admitindo que o comprimento da bobina é muito pequeno em comparação com o seu
diâmetro, determine a corrente que a deve percorrer para produzir um campo de 3x10-4
Wb/m2 no seu centro.
4. Uma corrente estacionária I passa num fio cilíndrico de raio R, muito comprido.
R
I
r
Calcule o campo de indução magnética, B , tanto no interior como no exterior do tubo,
nas duas seguintes situações:
a) a corrente está uniformemente distribuída sobre a superfície exterior do fio;
r
b) a corrente está distribuída de forma a que a densidade volumétrica de corrente, J ,
seja proporcional a r, que representa a distância medida a partir do fio (com r < R).
5. A figura seguinte representa o corte tranversal de um condutor cilíndrico muito
comprido, que tem uma cavidade igualmente cilíndrica no seu interior. O condutor é
r
percorrido por uma densidade de corrente estacionária J .
r
J
b
R
d
a)Comece por considerar que a concavidade é concêntrica com o condutor (d=0).
r
Determine o campo indução magnética, B , no condutor se a densidade de corrente
r
)
variar radialmemente segundo a expressão J = Kr 2 u z , onde K é uma constante e b ≤ r ≤
R.
b)Admita agora que o centro da cavidade se encontra a uma distância d do centro do
condutor (ver figura) e que a densidade de corrente é uniforme. Nestas condições,
r
determine o campo indução magnética, B , dentro da cavidade.
6. Considere dois solenóides coaxiais muito compridos, em que cada um é percorrido
por uma corrente estacionária I, mas circulando em sentidos contrários (ver figura). O
solenóide interior, de raio a, tem N1 espiras por unidade de comprimento, enquanto que
solenóide exterior, de raio b, tem N2 espiras.
r
Calcule o campo de indução magnética, B , em cada uma das seguintes três regiões:
a) no interior do solenóide de menor raio;
b) entre os dois solenóides;
c) no exterior dos solenóides.
MAGNETOSTÁTICA: LEI DE BIOT-SAVART
r
1.a) Determine o campo de indução magnética B num ponto P situado a uma distância
Z sobre o eixo que passa pelo centro de uma espira circular de raio R percorrida por
uma corrente estacionaria I, como se mostra na seguinte figura.
P
r
r
Z
R
r
I
dl
b) O campo de indução magnética no eixo de uma espira circular percorrida por uma
corrente estacionária I está longe de ser uniforme (diminui com o aumento de Z).
Contudo, pode produzir-se um campo mais uniforme utilizando-se duas espiras iguais
de raio R separadas por uma distancia s e percorridas por correntes da mesma
intensidade e circulando no mesmo sentido.
r
i) Determine o campo B em função de z e mostre que ∂B/∂z é igual a zero no ponto
intermédio entre as duas espiras (z=0).
ii) Determine qual deverá ser a distância entre as espiras, s, para que se verifique que
∂2B/∂z2=0 no ponto médio e determine o campo de indução magnética resultante.
2. Calcule o campo de indução magnética no eixo de um solenóide formado por um
enrolamento de N espiras por unidade de comprimento em torno de um tubo cilíndrico
de raio R, percorrido por uma corrente estacionária I. Exprima a sua resposta em termos
de θ1 e θ2 (ver figura indicada em baixo). Considere as espiras como sendo
essencialmente circulares. Qual é o campo no eixo de um solenóide infinito?
θ1
P
θ2
3. Calcule o campo de indução magnética num ponto P situado a uma distância z de um
fio que é percorrido por uma corrente estacionaria I (ver figura).
P
Z
r
r
dl
I
L
4. Determine o campo de indução magnética no centro de uma espira quadrada, de lado
2R, que é percorrida por uma corrente estacionaria I (ver figura ).
I
R
I
5.a) Determine o campo de indução magnética no centro de um polígono regular com n
lados que é percorrido por corrente estacionária I. Considere que R é a distância do
centro do polígono a qualquer um dos seus lados.
b) Mostre que a equação obtida na alínea anterior se reduz à do campo no centro de uma
espira considerando o limite n →∞.
6.Considere ume espira em forma de rectângulo, de lados 2A e 2L (sendo L>A),
percorrida por uma corrente estacionária I (ver figuras) .
Z
I
2L
2A
I
2L
2A
I
Figura 1
Figura 2
r
a) Calcule o campo de indução magnética, B , no centro da espira representada na figura
1.
r
b) Obtenha uma expressão para B quando L>>A. Compare essa expressão com a que
obteria se calculasse o campo de indução magnética no meio de dois fios condutores de
comprimento infinito percorridos pela mesma corrente I, mas em sentidos opostos.
r
c) Determine agora o campo de indução magnética, B , num ponto que se encontra a
uma distância Z do centro da espira (ver figura 2). Verifique o que obtém quando Z=0 e
compare com o resultado da primeira alínea.
7. Uma espira quadrada, de lado a, esta colocada a uma distancia b de um fio infinito
percorrido por uma corrente estacionaria I (ver figura).
a
a
I
b
a) Determine o fluxo do campo magnético, criado pela corrente I, na espira.
b) Se a espira for percorrida pela corrente estacionária I0, determine o sistema de forças
que actua sobre ela.
8. Uma espira quadrada de lado a, percorrida pela corrente estacionaria I, é livre de
rodar em torno do eixo dos zz, conforme mostra a seguinte figura.
z
r
B
I
r
Suponha que a espira esta mergulhada num campo de indução magnética B , uniforme e
perpendicular ao eixo dos ZZ.
a) Determine a resultante e o binário do sistema de forças que actua sobre a espira.
b) Como varia o fluxo do campo de indução magnética que atravessa a espira em
função do ângulo de que a espira roda?
c) A própria espira cria um campo magnético devido à corrente I que a percorre. Qual é
a direcção e o sentido desse campo? Determine o valor do campo no centro da espira.
d) Existe alguma posição de equilíbrio da espira? A posição é estável? Como se
posicionam os campos exterior e o criado pela espira?
e) Como se poderia proceder para que a espira rodasse indefinidamente?
CIRCUITOS MAGNÉTICOS, INDUTÂNCIA MÚTUA E AUTO-INDUTÂNCIA
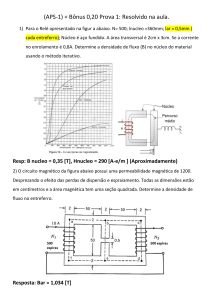
1. O circuito magnético esquematizado na figura é constituído por um núcleo formado
por uma liga de ferro-níquel e tem um entreferro de ar de 2 mm. As dimensões são as
indicadas na figura, sendo a dimensão transversal igual a 5 cm. O enrolamento tem
1000 espiras.
4 cm
I
12 cm
I
4 cm
6 cm
10cm
6 cm
Supondo que a secção recta do entreferro é 10% superior à secção recta do material
ferromagnético nas proximidades determine, assumindo uma permeabilidade magnética
relativa constante igual a 1000 em todo o circuito magnético:
a) a corrente necessária para obter uma indução magnética de 0,6 T no entreferro;
b) o valor da indução magnética no entreferro quando a corrente é 0,7 A.
2.Um anel de Rowland de ferro com 10 cm de diâmetro médio tem um entreferro com 1
mm de comprimento. Quando passa um acorrente estacionária por uma bobina com
1000 espiras enroladas no anel, o campo B de indução magnética tem o valor de 1 T.
Admitindo que o fluxo não varia no entreferro, detemine:
a) a permebilidade magnética relativa do ferro nestas condições
b) o campo H no interior do anel;
c) o quociente entre o campo H no entreferro e dentro do anel.
3.Considere o circuito magnético que se encontra representado na seguinte figura,
constituído por um material ferromagnético de permeabilidade magnética µ, onde se
coloca N espiras percorridas por uma corrente estacionária I no braço central do
circuito. A secção transversal deste circuito é constante.
D1
D1
I
D2
I
a)Obtenha o esquema equivalente deste circuito magnético em termos de relutâcias,
fluxos magnéticos e força magnetomotriz, indicando as expressões que permitem
calcular estas três grandezas.
r
b) Determine o fluxo magnético, Φ, e o campo de indução magnética, B , nos diferentes
ramos do circuito.
4.Considere um fio condutor muito comprido que se encontra no eixo de uma bobina
toroidal de secção rectangular (ver figura).
i
h
a
b
Admitindo que a bobina se encontra total e uniformemente coberta por N espiras,
determine a indutância mútua entre o fio condutor e a bobina.
5. Determine a auto-indutância por unidade de comprimento de um longo cabo coaxial
percorrido por uma corrente I (a corrente I percorre a superfície do condutor interior
num sentido e no sentido contrário a superfície do condutor exterior), sendo a o raio do
condutor interior e b o raio do condutor exterior (ver figura).
I
a
I
b
I
6. Calcule a indutância por unidade de comprimento de um condutor cilíndrico muito
longo, de secção recta de raio r0, percorrido por uma corrente de muito baixa frequência.
7. Numa linha de transmissão bifilar, os fios, ambos de raio r0, e separados por uma
distância d, são percorridos (em sentidos opostos) por uma corrente de frequência muito
baixa.
a) Determine o coeficiente de auto-indução por unidade de comprimento da linha;
b) Calcule a indutância por unidade de comprimento da linha.
8.Uma linha de transmissão é formada por lâminas metálicas muito finas de largura W e
separadas por uma distância s (em que s <<W). A corrente de muito baixa frequência
percorre uma lâmina num sentido e a outra lâmina em sentido contrário.
a) Determine a capacidade por unidade de comprimento, C0, da linha;
b) Determine a indutância por unidade de comprimento, L0, da linha;
c) Verifique que o produto L0C0 é igual a ε0µ 0. Calcule o valor numérico deste produto e
comente o resultado obtido.
d) Se as lâminas estiverem isoladas uma da outra por meio de um material não condutor
de permitividade ε e permeabilidade magnética µ, qual é o valor do produto L0C0?
9. Considere um anel de Rowland com N espiras, com uma relutância e um campo B no
seu interior.
a) Mostre que a energia armazenada num anel de Rowland á dada por 1/2RΦ2, onde Φ
representa o fluxo, através de uma secção transversal do anel;
b) verifique que a auto-indutância do anel é dada por L=N2/R.
10.Considere o anel de Rowland nas condições descritas na pergunta 2. Determine:
a) a enrgia armazenada no interior do anel;
b) a anergia armazenada no entreferro;
c) o coeficiente de auto-indução do sistema.
ELECTRODINÂMICA: LEI DE INDUÇÃO E EQUAÇÕES DE MAXWELL
1) Considere uma espira rectangular de área A, tal como se mostra na figura 1. O vector
r
campo de indução magnética, B , é normal ao plano da espira e uniforme sobre toda a
sua superfície. Contudo, a sua intensidade varia harmonicamente no tempo de acordo
com a expressão B(t)=B0cos(ωt), onde B0 é a amplitude de B e ω representa a
frequência angular do movimento harmónico.
r
B
Área A
Determine a força electromotriz induzida na espira.
2.a) Considere a espira rectangular esquematizada na figura abaixo indicada. A largura
L da espira é constante, mas o seu comprimento x aumenta uniformemente no tempo
devido ao movimento, com velocidade v, do segmento condutor deslizante, AB . O
r
vector indução magnética B é constante, normal ao plano da espira e uniforme sobre
toda a superfície da espira. Calcule a força electromotriz induzida na espira.
A
r
B
L
B
x
b) Qual é a forca electromotriz induzida na espira, sabendo que o segmento condutor
r
deslizante se desloca com velocidade uniforme v e que o vector indução magnética B é
uniforme sobre a superfície da espira, variando no tempo segundo a relação
B(t)=B0cos(ωt).
3.a) Considere uma espira rectangular, de largura R e comprimento L, colocada sob a
r
acção de um campo de indução magnética, B , uniforme (ver figura ).
Eixo
O´
ω
r
B
R
L
O
Sabendo que a espira roda em torno do eixo OO' com velocidade angular, ω, constante,
determine a força electromotriz induzida na espira;
b) Suponha que o campo de indução magnética em que a espira está mergulhada varia
no tempo de acordo com a relação B(t)=B0cos(ωt), em que ω tem o mesmo valor da
frequência angular de rotação da espira. No instante inicial t=0, tem-se B=0 e θ=0 (ver
figura seguinte). Determine a força electromotriz induzida na espira.
r
B
θ
v
Eixo
R
4. Na figura abaixo, encontra-se esquematizada a cabeça de um gira-discos, que é
constituída por uma bobina com N espiras, cada uma com área S, movendo-se num
campo de indução magnética. Os sulcos na superfície do disco deflectem a agulha
produzindo uma rotação na bobina.
r
B
L
x
Disco
a) Mostre que para pequenos ângulos de deflexão (x<<L) a diferença de potencial nos
terminais da bobina é descrito pela expressão (NBS/L)(dx/dt).
b) Se N=10, S=0,1 cm2, B=0,3T, L=0,7 cm e x(t)=0,01sin (2πft) – com x em cm-, sendo
f a frequência do som gravado. Qual é a diferença de potencial para os seguintes valores
de frequência: (i) 100 Hz; (ii) 1000 Hz; (iii) 10000 Hz?
5. Uma espira quadrada de lado s, possui uma resistência R e está situada a uma
distância s de um fio infinito percorrido por uma corrente estacionária I (ver figura).
s
s
I
a) Suponha que, a certa altura, o fio é cortado. Em que sentido é que circula a corrente
eléctrica induzida na espira e qual é a carga total que passa num dado ponto da espira
enquanto essa corrente flui?
b) Repita a alínea anterior, mas admitindo que a intensidade de corrente diminui
gradualmente, de acordo com a seguinte relação:
(1 − αt)I
I (t ) = 
 0
se
se
0 ≤ t ≤ 1α
t > 1α
6) Considere o circuito magnético representado na figura seguinte.
ε2
ε1
N2
N1
Mostre que se se aplicar uma força electromotriz, ε1, oscilante no braço esquerdo desta
armadura, se obtém uma força electromtriz do lado direito com o valor ε2=N2/N1ε1, onde
N1 e N2 representam o número de espiras dos esquerdo e direito da armadura.
Esta relação constitui o princípio de funcionamento de um transformador.
7) Considere um cabo coaxial formado por um fio condutor muito longo e por um
cilindro condutor oco, concêntrico com o fio e de raio R. Uma corrente alternada
sinusoidal, I(t)=I0cos(ωt), sendo ω a frequência angular, percorre o fio num sentido e
retorna no cilindro exterior.
a) Qual é a direcção (radial, circunferencial ou longitudinal) em que aponta o vector
campo eléctrico induzido?
b) Determine o vector campo eléctrico induzido em função da distância r ao eixo do
cabo;
r
c)Obtenha a densidade de corrente de deslocamento, J d ;
d) Sabendo que o cilindro exterior tem um diâmetro de 2 mm, qual deve ser o valor da
frequência, f, da corrente para que Id, seja 1% de I?
(Observação: O resultado desta alínea permite explicar porque é que Faraday nunca
descobriu as correntes de deslocamento e porque é que, em geral, se pode ignorar estas
correntes quando a sua frequência é baixa).
8) A uma frequência f=4x108 Hz=400 MHz, a permitividade eléctrica da água do mar é
ε=81ε0, a sua permeabilidade magnética é µ=µ0=4π x10-7N/A2 e a sua resistividade vale
ρ=0,23Ωm.
Nesta situação, compare os valores da corrente de condução e de deslocamento.
(Sugestão: considere um condensador de placas paralelas imerso na água do mar e
submetido a uma tensão sinusoidal do tipo V(t)=V0cos(2πft).)
9) Um condensador de placas paralelas circulares, de raio a e separadas por uma
distância s, está inserido num longo fio rectilíneo, onde se faz passar uma corrente
eléctrica estacionária de intensidade I, tal como se indica na figura.
a
s
r
À medida que o condensador é carregado, determine o campo de indução magnética, B ,
que é induzido na região entre as placas a uma distância r (com r<a) do centro.