1. A massa m 2 é puxada para a direita por uma força horizontal, F

UNIVERSIDADE FEDERAL DE GOIÁS
INSTITUTO DE FÍSICA
PROGRAMA DE PÓS-GRADUAÇÃO
Campus Samambaia, C. P. 131, Goiânia-GO, Brasil, CEP 74002-970
Fone: (062) 3521-1014 ramal 200, 204 e 247 (Fax)
www.if.ufg.br/posgraduacao
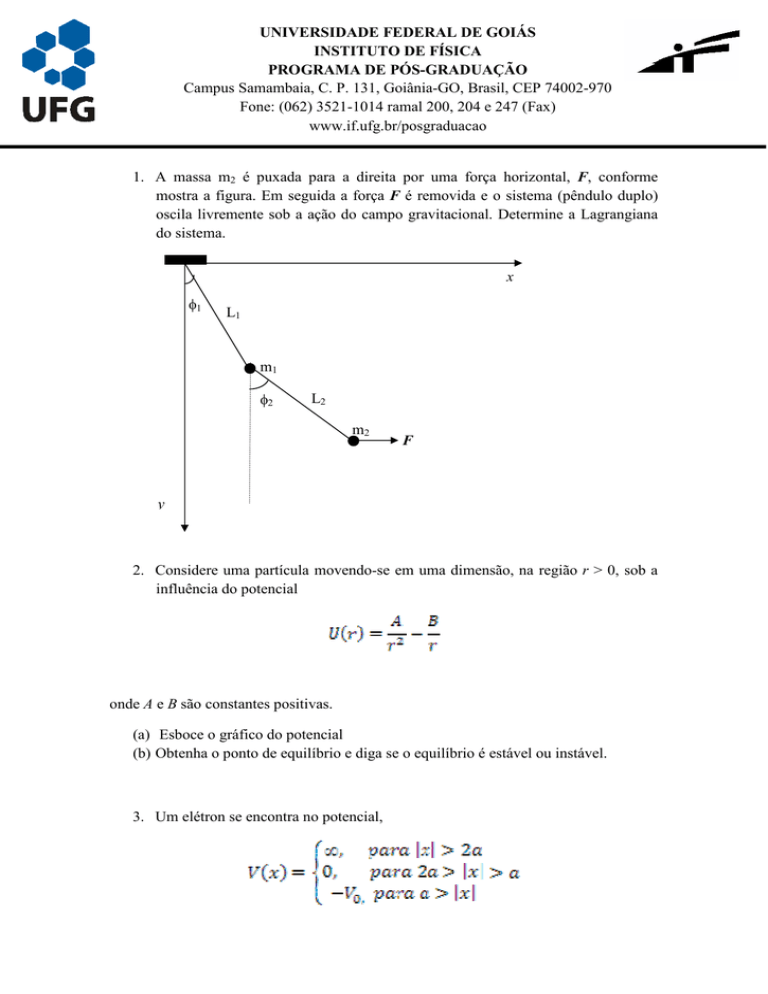
1. A massa m2 é puxada para a direita por uma força horizontal, F, conforme
mostra a figura. Em seguida a força F é removida e o sistema (pêndulo duplo)
oscila livremente sob a ação do campo gravitacional. Determine a Lagrangiana
do sistema.
x
φ1
L1
m1
φ2
L2
m2
F
y
2. Considere uma partícula movendo-se em uma dimensão, na região r > 0, sob a
influência do potencial
onde A e B são constantes positivas.
(a) Esboce o gráfico do potencial
(b) Obtenha o ponto de equilíbrio e diga se o equilíbrio é estável ou instável.
3. Um elétron se encontra no potencial,
(a) Para E < 0, determine o conjunto de equações que de forma única fornecem
as soluções pares da equação de Schrödinger.
(b) Mostre o procedimento gráfico para se determinar as energias
4. Considere uma partícula de carga +e movendo-se sob a ação do potencial
harmônico isotrópico tridimensional
(a) Determine a degenerescência dos três primeiros níveis com energias
distintas.
ao sistema, determine os novos
(b) Ao aplicar um campo elétrico
autovetores e as novas autoenergias da partícula.
5. (a) Considere uma espira circular de raio R no plano xy, centrada na origem do
sistema de coordenadas, por onde passa uma corrente I orientada no sentido antihorário. Calcule o campo magnético gerado por esta corrente ao longo do eixo z
que passa pela origem perpendicularmente ao plano xy. (b) Agora a corrente é
desligada e a espira é carregada com densidade de carga uniforme λ. Calcule o
campo elétrico gerado pela mesma espira. (c) Compare a razão entre os campos
elétrico e magnético na origem e nos pontos a uma altura z = R e z = -R acima e
abaixo do plano x-y.
6. Deduza a equação de onda eletromagnética para os campos elétricos e
magnéticos na presença de matéria e no vácuo.
7. Para um gás perfeito monoatômico, determine a expressão correta para a energia
livre de Helmholtz.
8. Considere a seguinte construção: um conjunto de cópias idênticas de um gás
mantido em um cilindro fechado com paredes fixas e em contato com um
termostato. A única diferença entre as cópias está no estado microscópico do gás
dentro do cilindro. Conforme a definição de Gibbs, que tipo de ensemble temos
aqui, e qual é a expressão fundamental que relaciona o comportamento
microscópico com o macroscópico?
1
Coordenação da Pós-Graduação do Instituto de Fı́sica - UFG
Julho de 2011
Formulário
Equações de Maxwell e Lei de Biot-Savart
∇.B = 0
ρ
∇.E =
0
∂B
∂t
1 ∂E
∇×B= 2
+ µ0~j
c ∂t
µ0 dl1 × (r2 − r1 )
dB(r2 ) =
4π |r2 − r1 |3
∇×E=−
(1)
(2)
(3)
(4)
(5)
Identidades
∇.(P × Q) = Q.(∇ × P) − P.(∇ × Q)
∇ × (∇ × E) = ∇.(∇.E) − ∇2 E
(6)
(7)