Solução

www.fisicaexe.com.br
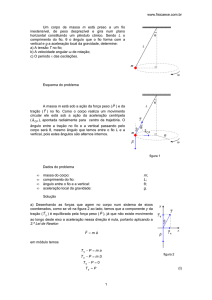
Um corpo de massa m está suspenso por um fio,
inextensível e de massa desprezível, na ponta de um suporte em
forma de L invertido verticalmente, com a barra horizontal medindo
D, conforme figura. Este conjunto gira em torno do eixo vertical do
suporte. Sendo L o comprimento do fio e g a aceleração local da
gravidade, determine a velocidade angular com que o conjunto deve
girar para que o ângulo θ que o fio forma com a vertical seja 90o.
Esquema do problema
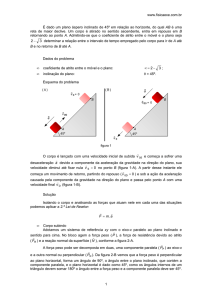
A massa m está sob a ação da força peso ( P
) e da tração ( T ) no fio. Como o corpo realiza um
movimento circular ele está sob a ação da aceleração
centrípeta ( a CP ), apontada radialmente para centro
da trajetória. O ângulo entre a tração no fio e a vertical
passando pelo corpo será θ, mesmo ângulo que
temos entre o fio L e a vertical, pois estes ângulos são
alternos internos.
figura 1
Dados do problema
•
•
•
•
massa do corpo:
comprimento do fio:
componente do suporte horizontal:
aceleração local da gravidade:
m;
L;
D;
g.
Solução
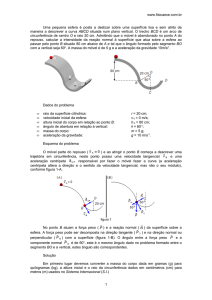
Desenhando as forças que agem no corpo num sistema de eixos
coordenados (figura 2) e aplicando a 2.ª Lei de Newton
F = ma
T−P = m a
T x  T y −m g = m a
T x iT y j−m g j = m  a ´ x ia´ y j 
T x iT y j−m g j = m a´ x im a ´ y j
onde T x e a x são as componentes da tração e da aceleração na direção i e
T y e a y são as componentes da tração e da aceleração na direção j.
Separando as componentes
• direção I
1
figura 2
www.fisicaexe.com.br
T x = m a´ x
(I)
T x = T sen θ
(II)
o módulo da componente T x é dado por
e a componente da aceleração a x é a aceleração centrípeta a C P responsável pelo corpo
fazer a curva, substituindo esta aceleração e a expressão (II) em (I), temos
•
T senθ = m a C P
(III)
T y−m g = m a ´ y
(IV)
direção j
o módulo da componente T y é dado por
T y = T cos θ
(V)
com não existe movimento nesta direção a componente da aceleração é nula ( a y = 0 ),
substituindo esta aceleração e a expressão (V) em (IV), temos
T cos θ−m g = m .0
T cos θ−m g = 0
T cos θ = m g
(VI)
Dividindo a expressão (III) por (VI), obtemos
T sen θ m a C P
=
T cosθ
mg
aC P
tg θ =
g
a C P = g tgθ
(VII)
O módulo da aceleração centrípeta é dada por
aC P =
v
r
2
(VIII)
a velocidade tangencial v é dada pro
v = r
(IX)
substituindo (IX) em (VIII), temos
2
 r 
r
2 2
 r
aCP=
r
2
aC P =  r
aC P =
(X)
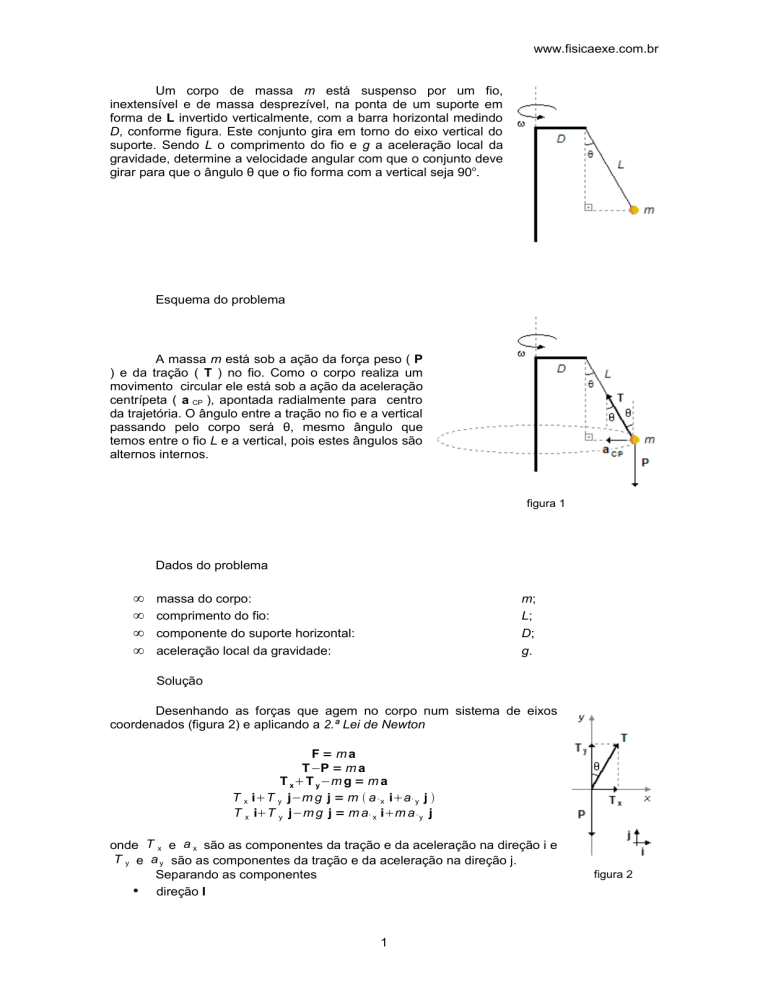
onde r representa a distância do corpo ao eixo de rotação dado pela soma do comprimento do
suporte horizontal D e do deslocamento da massa R provocado pela rotação (figura 3)
2
www.fisicaexe.com.br
r = DR
Da figura 3 podemos
deslocamento corpo como
(XI)
escrever
a
distância
R
R
L
R = L sen θ
do
sen θ =
(XII)
substituindo a expressão (XII) em (XI)
r = DL sen θ
(XIII)
figura 3
substituindo a expressão (XIII) em (X) e esta em (VII), temos
2
  DL sen θ  = g tg θ
g tg θ
2
 =
 D L sen θ 
1
´
g tgθ
2
=
DL sen θ
[
]
(XIV)
o
Queremos saber a velocidade angular para a qual o ângulo será θ = 90 =
π
, para
2
este ângulo o valor da tangente da expressão (XIV) tende ao infinito, assim
lim  = lim
θ
π
2
θ
π
2
[
g tg θ
D L sen θ
]
´
1
2
=
[
g tg
π
2
DL sen
]
´
π
2
1
2
=
[
g.∞
D L . 1
]
´
1
2
=∞
v =∞
Observação: na prática o ângulo nunca chega a 90o, pois para isso seria preciso uma
velocidade angular infinita, por mais rápido que se gire o corpo maior será o ângulo que ele
forma com a vertical, no entanto nunca ficará perfeitamente horizontal.
3