Solução

www.fisicaexe.com.br
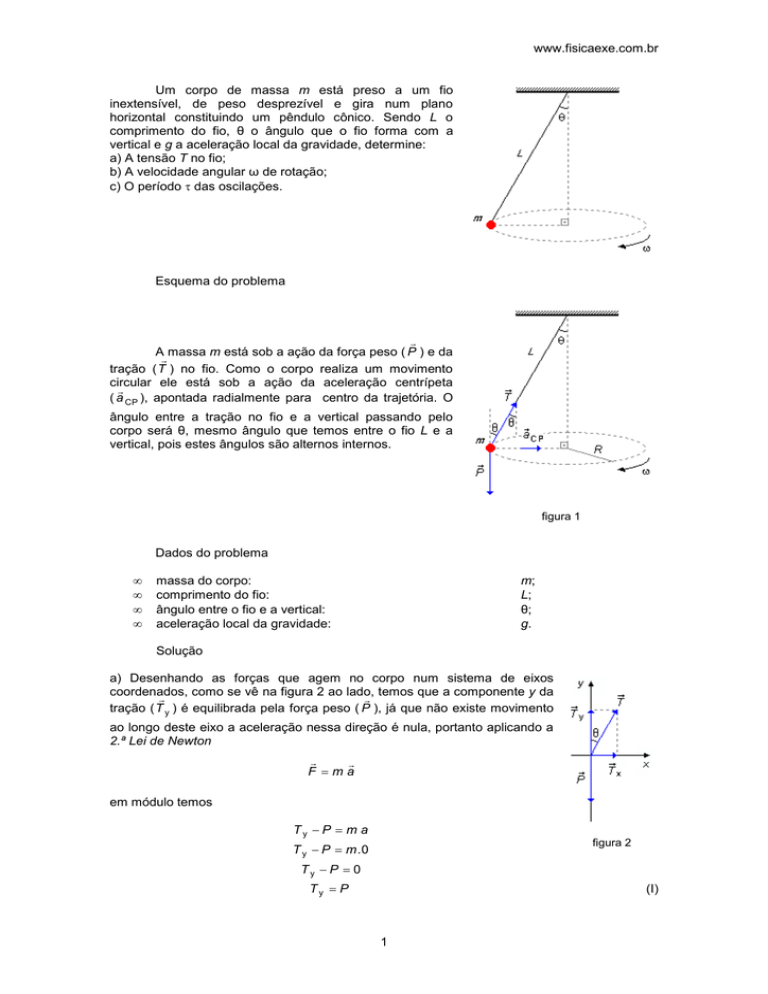
Um corpo de massa m está preso a um fio
inextensível, de peso desprezível e gira num plano
horizontal constituindo um pêndulo cônico. Sendo L o
comprimento do fio, θ o ângulo que o fio forma com a
vertical e g a aceleração local da gravidade, determine:
a) A tensão T no fio;
b) A velocidade angular ω de rotação;
c) O período τ das oscilações.
Esquema do problema
r
A massa m está sob a ação da força peso ( P ) e da
r
tração ( T ) no fio. Como o corpo realiza um movimento
circular ele está sob a ação da aceleração centrípeta
r
( a CP ), apontada radialmente para centro da trajetória. O
ângulo entre a tração no fio e a vertical passando pelo
corpo será θ, mesmo ângulo que temos entre o fio L e a
vertical, pois estes ângulos são alternos internos.
figura 1
Dados do problema
•
•
•
•
m;
L;
θ;
g.
massa do corpo:
comprimento do fio:
ângulo entre o fio e a vertical:
aceleração local da gravidade:
Solução
a) Desenhando as forças que agem no corpo num sistema de eixos
coordenados, como se vê na figura 2 ao lado, temos que a componente y da
r
r
tração ( T y ) é equilibrada pela força peso ( P ), já que não existe movimento
ao longo deste eixo a aceleração nessa direção é nula, portanto aplicando a
2.ª Lei de Newton
r
r
F =ma
em módulo temos
Ty − P = m a
figura 2
T y − P = m .0
Ty − P = 0
Ty = P
(I)
1
www.fisicaexe.com.br
r
Sendo o ângulo θ medido entre o vetor T e o eixo y (ao contrário do que se faz
usualmente, em que se mede um ângulo a partir do eixo x), temos que o módulo da
componente da tração na direção de y será
T y = T cos θ
(II)
e o módulo da força peso será igual a
P=mg
(III)
substituindo (II) e (III) em (I) obtemos
T cos θ = m g
T =
mg
cos θ
b) Pela figura 2 escrevemos a 2.ª Lei de Newton para um corpo em movimento circular (onde
atua a aceleração centrípeta)
r
r
F CP = m a CP
r
r
temos que a componente do vetor T ao longo do eixo x ( T x ) , é a única força responsável
r
pela força centrípeta F CP , ou seja em módulo
T x = m a CP
(IV)
T x = T sen θ
(V)
r
o módulo de T x será dado por
substituindo T pelo valor encontrado no item anterior temos
Tx =
mg
sen θ
cos θ
(VI)
A aceleração centrípeta será dada por
a CP =
v2
R
(VII)
substituindo (VI) e (VII) em (IV)
mg
v2
sen θ = m
cos θ
R
simplificando a massa de ambos os lados da igualdade
g
v2
sen θ =
R
cos θ
A velocidade será dada pro
2
(VIII)
www.fisicaexe.com.br
v =ωR
(IX)
substituindo (IX) em (VIII)
(ωR )
g
sen θ =
R
cos θ
2
g
ω2 R 2
sen θ =
R
cos θ
g
sen θ = ω 2 R
cos θ
(X)
O valor do raio (R) da trajetória não é fornecido pelo problema, é
preciso encontrar esse valor em função dos dados do problema, pela
figura 3 vemos que
sen θ =
cateto oposto R
=
hipotenusa
L
R = L sen θ
(IX)
substituindo (XI) em (X)
g
sen θ = ω 2 L sen θ
cos θ
simplificando o seno de ambos os lados da igualdade
g
= ω2 L
cos θ
g
cos θ
ω2 L =
ω2 =
ω=
g
L cos θ
g
L cos θ
c) O período τ pode ser calculado lembrando que
ω=
2π
τ
usando o valor da velocidade angular ω obtido no item anterior, escrevemos
2π
g
=
L cos θ
τ
L cos θ
g
τ=2π
3
figura 3