Solução

www.fisicaexe.com.br
Um pêndulo simples é constituído por um corpo de massa 1,5 kg preso numa
extremidade de um fio de cobre. Mantida fixa a outra extremidade desse fio, afasta-se o
pêndulo de 60o da posição de equilíbrio. Observa-se então que o fio se rompe no instante
preciso que em que passa pela vertical de equilíbrio. Sabendo-se que a tensão de rompimento
do cobre é 20 000 N/cm 2 e a aceleração da gravidade é 10 m/s 2, calcule o diâmetro do fio.
Dados do problema
•
•
•
•
•
massa do corpo:
velocidade inicial do corpo:
ângulo de deslocamento em relação à vertical:
tensão de rompimento:
aceleração da gravidade:
m = 1,5 kg;
v 0 = 0 m/s;
θ = 60 o;
T R = 20 000 N/cm 2;
g = 10 m/s 2.
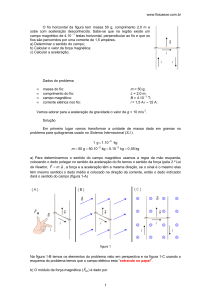
Esquema do problema
Chamamos o ponto de onde o
corpo liberado de ponto A, o ponto onde
o corpo passa pela vertical de equilíbrio
de ponto B e o comprimento do fio será
L.
Adotamos que no momento em
que o corpo é liberado sua velocidade é
nula ( v 0 = 0 ).
Solução
Em primeiro lugar devemos
converter a tensão de rompimento dada
figura 1
em newtons por centímetro quadrado
( N / cm 2 ) para newtons por metro quadrado ( N / m 2 ) usado no Sistema Internacional (S.I.)
2
N  100 cm 
N 10000 cm 2
= 20 000
=
2.
2
2.
2
cm
1m 
cm
1m
N
4
4 N
8 N
= 20 000.10 000 2 = 2. 10 .1 .10
2 = 2 .10
2
m
m
m
T ´ R = 20000
O problema nos
fornece
a tensão
de
rompimento do fio, que é
dada em termos de força
(tensão que atua no fio
devido a massa presa nele)
por unidade de área (figura
2). Se multiplicarmos a
tensão de rompimento pela
área transversal do fio
termos a tensão total que
atua nele no momento do
rompimento, assim
T =T RA
figura 2
(I)
Para determinarmos a velocidade quando o corpo passa pela vertical usamos o
Princípio da Conservação da Energia Mecânica, a energia mecânica inicial, no ponto em que o
corpo é liberado (à 60 o da vertical), deve ser igual a energia mecânica final, no ponto em que
passa pela vertical de equilíbrio
1
www.fisicaexe.com.br
À
B
EM= E M
E E ÀC = E BP E BC
2
2
mv A
mv B
m g h A
= m g h B
2
2
À
P
simplificando a massa m de ambos os lados da igualdade, temos
2
g h A
2
vA
vB
= g h B
2
2
(II)
Adotando um Nível de Referência (N.R.) no
ponto onde o corpo passa pela vertical (figura 3), a
altura deste ponto será nula (h B = 0), como a velocidade
inicial também é nula (v A = v 0 = 0), a expressão (II) se
reduz a
2
2
vB
0
= g .0
2
2
v 2B
g h A 0 = 0
2
2
vB
gh A =
2
2
v B = 2gh A
g h A
(III)
figura 3
O ângulo formado pelo fio quando o corpo está na posição A e pelo segmento AB é α
(figura 4-A), o ângulo formado pelo fio quando o corpo está na posição B e pelo segmento AB
também é α. A soma dos ângulo internos de um triângulo é 180 o , então temos,
o
o
o
o
o
o
o
o
60  = 180 ⇒ 60 2  = 180 ⇒ 2  = 180 −60 ⇒ 2  = 120 ⇒  = 60 . Como os três
ângulos são iguais, os três lado também são, então, o segmento AB também vale L, é um
triângulo equilátero.
figura 4
Quando o corpo passa pela vertical o fio L é perpendicular ao Nível de Referência
(forma um ângulo de 90 o), como o ângulo entre o fio e o segmento AB é 60 o, o ângulo β entre
o segmento AB e o Nível de Referência será 60 o = 90 o ⇒  = 90 o −60 o ⇒  = 30 o . Então a
altura do ponto A ( h A ) em relação ao Nível de Referência será pela figura 4-B
cateto oposto h A
=
hipotenusa
L
hA
o
sen 30 =
L
sen  =
2
www.fisicaexe.com.br
1
, temos
2
o
lembrando da Trigonometria que sen 30 =
1 hA
=
2
L
L
hA=
2
(IV)
substituindo (IV) em (III), obtemos
L
2
2
v B = gL
2
v B = 2g
(V)
O pêndulo descreve um arco de circunferência (figura 5),
analisando as forças que atuam no sistema podemos aplicar a 2.a Lei de
Newton
 CP = m
F
aC P
Adotamos o sentido da aceleração centrípeta positivo, assim a
resultante da força centrípeta será
F C P = T −P
(VI)
sendo a força peso dada por P = m g e a tensão dada pela expressão (I),
temos
F C P = T R A−m g
(VII)
figura 5
A aceleração centrípeta, no ponto B, é dada por
2
aC P =
vB
r
(VIII)
substituindo a velocidade encontrada em (V) em (VIII) e sendo o raio da circunferência igual ao
comprimento do fio do pêndulo (r = L), obtemos
gL
L
aC P = g
aC P =
Substituindo as expressões (VII) e (IX) a 2.a Lei de Newton fica
T R A−m g = m g
T R A = m gm g
T R A = 2mg
2mg
A=
TR
substituindo os valores dados no problema, temos finalmente
2 .1,5 .10
8
2.10
30
−8
A=
.10
2
−8
2
A = 15.10 m
A=
3
(IX)
www.fisicaexe.com.br
Admitindo que o fio tem uma secção transversal circular, a área de um círculo é dada
por
A= πr
2
adotando π = 3,14 e usando o valor da área encontrado acima
15. 10
−8
= 3,14r
15. 10 −8
2
r =
3,14
r 2 ≃ 4,8 . 10 −8
2
−8
r ≃  4,8 . 10
r ≃ 2,2 .10 −4 m
o diâmetro do fio será dado por
d = 2r
substituindo o valor do raio acima
d = 2 . 2,2 . 10
d = 4,4 . 10
4
−4
−4
m
2