Solução

www.fisicaexe.com.br
Uma pequena esfera é posta a deslizar sobre uma superfície lisa e sem atrito de
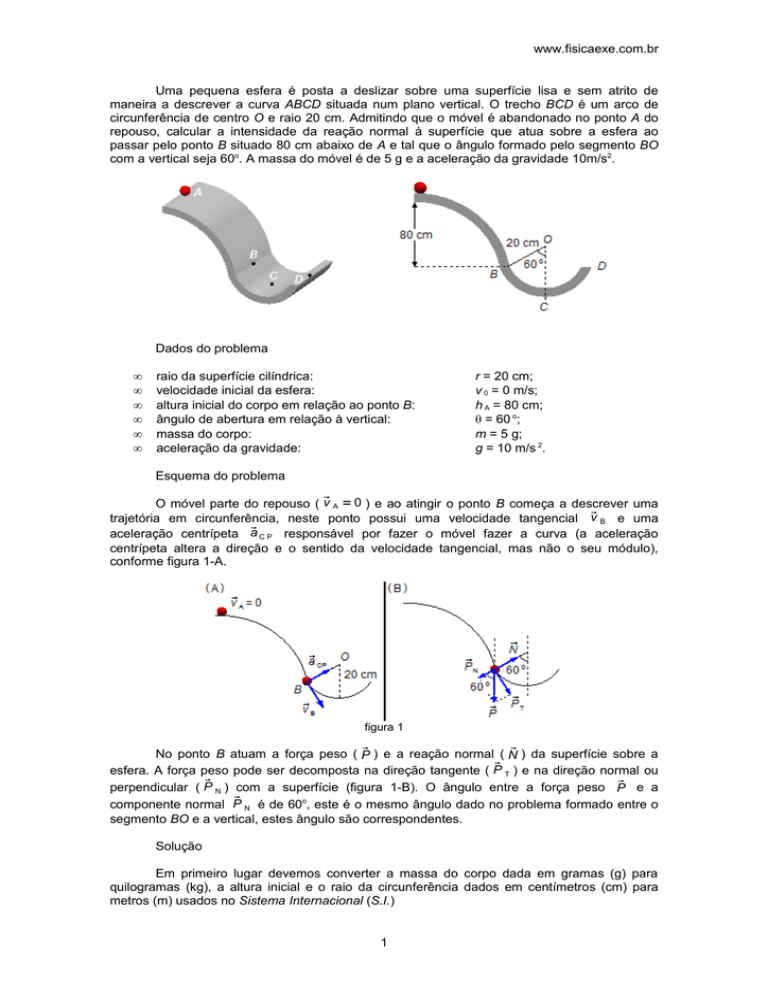
maneira a descrever a curva ABCD situada num plano vertical. O trecho BCD é um arco de
circunferência de centro O e raio 20 cm. Admitindo que o móvel é abandonado no ponto A do
repouso, calcular a intensidade da reação normal à superfície que atua sobre a esfera ao
passar pelo ponto B situado 80 cm abaixo de A e tal que o ângulo formado pelo segmento BO
com a vertical seja 60o. A massa do móvel é de 5 g e a aceleração da gravidade 10m/s2.
Dados do problema
•
•
•
•
•
•
raio da superfície cilíndrica:
velocidade inicial da esfera:
altura inicial do corpo em relação ao ponto B:
ângulo de abertura em relação à vertical:
massa do corpo:
aceleração da gravidade:
r = 20 cm;
v 0 = 0 m/s;
h A = 80 cm;
θ = 60 o;
m = 5 g;
g = 10 m/s 2.
Esquema do problema
v A = 0 ) e ao atingir o ponto B começa a descrever uma
O móvel parte do repouso ( 
v B e uma
trajetória em circunferência, neste ponto possui uma velocidade tangencial 
a C P responsável por fazer o móvel fazer a curva (a aceleração
aceleração centrípeta 
centrípeta altera a direção e o sentido da velocidade tangencial, mas não o seu módulo),
conforme figura 1-A.
figura 1
 ) e a reação normal ( N
 ) da superfície sobre a
No ponto B atuam a força peso ( P

P
esfera. A força peso pode ser decomposta na direção tangente ( T ) e na direção normal ou
 N ) com a superfície (figura 1-B). O ângulo entre a força peso P
 e a
perpendicular ( P
o

componente normal P N é de 60 , este é o mesmo ângulo dado no problema formado entre o
segmento BO e a vertical, estes ângulo são correspondentes.
Solução
Em primeiro lugar devemos converter a massa do corpo dada em gramas (g) para
quilogramas (kg), a altura inicial e o raio da circunferência dados em centímetros (cm) para
metros (m) usados no Sistema Internacional (S.I.)
1
www.fisicaexe.com.br
m = 5 g.
h ´ A = 80 cm.
r = 20 cm.
1 kg
−3
= 5 .10 kg
1000 g
1m
1
−2
−1
= 8 . 10 .10 kg = 8 .10 m
100 cm
1m
1
−2
−1
= 2 . 10 . 10 kg = 2 .10 m
100 cm
Para determinarmos a velocidade no ponto B usamos o Princípio da Conservação da
Energia Mecânica, a energia mecânica no ponto A deve ser igual a energia em B
À
B
EM= E M
À
E P E ÀC = E BP E BC
2
2
mv A
mv B
m g h A
= m g h B
2
2
simplificando a massa m de ambos os lados da igualdade, temos
2
g h A
2
vA
vB
= g h B
2
2
(I)
Adotando um Nível de Referência (N.R.) no ponto B (figura 2), a altura deste ponto será
nula (h B = 0), como a velocidade inicial também é nula (v A = 0), a expressão (I) se reduz a
2
2
vB
0
= g .0
2
2
v 2B
g h A 0 = 0
2
2
v
gh A = B
2
2
v B = 2gh A
g h A
(II)
figura 2
No ponto B a esfera começa a descrever uma trajetória circular, aplicando a 2.a Lei de
Newton
 CP = m
F
aCP
Da figura 1-B adotamos o sentido positivo para o centro O da circunferência, assim a
resultante da força centrípeta será, em módulo
F C P = N−P N
(III)
 N ) será dada por
a componente do peso na direção normal ( P
P N = P cos 60
o
(IV)
o
sendo a força peso dada por P = m g e lembrando da Trigonometria que cos 60 =
1
2
substituindo estes valores na expressão (IV), temos
1
2
mg
P N=
2
P N= mg
substituindo a expressão (V) em (III), obtemos
2
(V)
www.fisicaexe.com.br
F C P = N−
mg
2
(VI)
A aceleração centrípeta, no ponto B, é dada por
2
aCP =
vB
r
(VII)
substituindo a velocidade encontrada em (II) em (VII), temos
aC P =
2gh A
r
(VIII)
Substituindo as expressões (VI) e (VIII) a 2.a Lei de Newton fica, em módulo
2g h A
mg
=m
2
r
2g hA mg
N =m

r
2
N−
substituindo os valores dados no problema, temos finalmente
−1
−3
2 .10. 8 . 10
5. 10 . 10

−1
2
2. 10
−3
−1
1
−3
N = 5 .10 . 80.10 . 10 5. 10 . 5
−3
−3
N = 400. 10  25. 10
−3
N = 425 . 10
N = 5 . 10 −3 .
N = 0,425 N
3