Solução

www.fisicaexe.com.br
É dado um plano áspero inclinado de 45º em relação ao horizonte, do qual AB é uma
reta de maior declive. Um corpo é atirado no sentido ascendente, entra em repouso em B
retornando ao ponto A. Admitindo-se que o coeficiente de atrito entre o móvel e o plano seja
2−
3 determinar a relação entre o intervalo de tempo empregado pelo corpo para ir de A até
B e no retorno de B até A.
Dados do problema
•
coeficiente de atrito entre o móvel e o plano:
µ = 2−
•
inclinação do plano:
θ = 45º.
3;
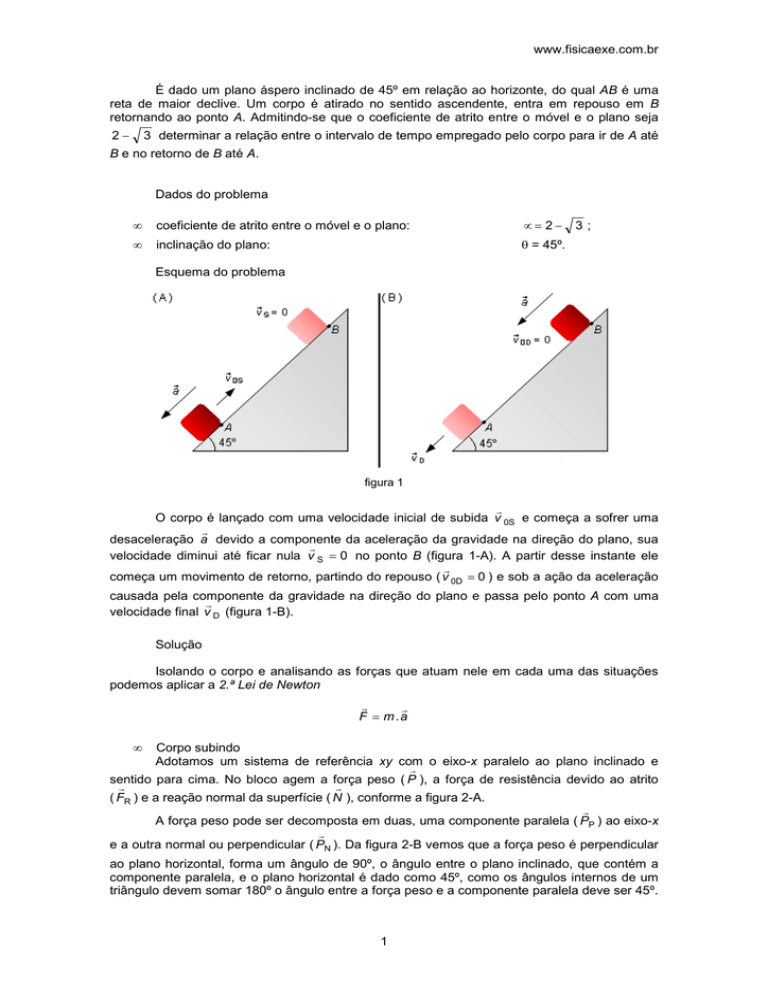
Esquema do problema
figura 1
r
O corpo é lançado com uma velocidade inicial de subida v 0S e começa a sofrer uma
r
desaceleração a devido a componente da aceleração da gravidade na direção do plano, sua
r
velocidade diminui até ficar nula v S = 0 no ponto B (figura 1-A). A partir desse instante ele
r
começa um movimento de retorno, partindo do repouso ( v 0D = 0 ) e sob a ação da aceleração
causada pela componente da gravidade na direção do plano e passa pelo ponto A com uma
r
velocidade final v D (figura 1-B).
Solução
Isolando o corpo e analisando as forças que atuam nele em cada uma das situações
podemos aplicar a 2.ª Lei de Newton
r
r
F = m .a
•
Corpo subindo
Adotamos um sistema de referência xy com o eixo-x paralelo ao plano inclinado e
r
sentido para cima. No bloco agem a força peso ( P ), a força de resistência devido ao atrito
r
r
( FR ) e a reação normal da superfície ( N ), conforme a figura 2-A.
r
A força peso pode ser decomposta em duas, uma componente paralela ( PP ) ao eixo-x
r
e a outra normal ou perpendicular ( PN ). Da figura 2-B vemos que a força peso é perpendicular
ao plano horizontal, forma um ângulo de 90º, o ângulo entre o plano inclinado, que contém a
componente paralela, e o plano horizontal é dado como 45º, como os ângulos internos de um
triângulo devem somar 180º o ângulo entre a força peso e a componente paralela deve ser 45º.
1
www.fisicaexe.com.br
No triângulo à direita temos que a componente normal faz com o plano inclinado um ângulo de
90º então o ângulo entre a força peso e a componente normal deve medir 45º, é um ângulo
complementar.
figura 2
Desenhamos as forças num sistema de eixos coordenados, figura 2-C.
Na direção y não há movimento, a reação normal e a componente normal do peso se
equilibram, em módulo temos
N = PN
N = P cos 45°
N = M g cos 45°
(I)
Na direção x escrevemos a 2.ª Lei de Newton em módulo para encontrar a aceleração
do bloco subindo ( a S )
−FR − PP cos 45° = M a S
−FR − M g cos 45° = M a S
(II)
A força de resistência devido ao atrito é dada por
FR = µ . N
(III)
substituindo o valor da reação normal (I) em (III) e colocando o resultado em (II), temos a
expressão para a aceleração do corpo durante a subida
−µ N − PP sen 45° = M a S
− µ M g cos 45° − M g sen 45° = M a S
a S = −µ g cos 45° − g sen 45°
(IV)
•
Corpo descendo
Analogamente temos o mesmo sistema de referência da situação anterior. No bloco
r
agem as mesmas forças, apenas a força de resistência ( FR ) está no sentido contrário, figura 3A.
Do mesmo modo a força peso pode ser decomposta em duas sendo válido o esquema
da figura 2-B
Desenhamos as forças num sistema de eixos coordenados, figura 3-B.
Na direção y é válida a mesma expressão (I) encontrada anteriormente.
2
www.fisicaexe.com.br
figura 3
Na direção x aplicamos a 2.ª Lei de Newton em módulo para encontrar a aceleração do
bloco descendo ( a D )
FR − PP sen 45° = M a D
FR − M g sen 45° = M a D
(V)
Usando a expressão para a força de resistência dada em (III) e a reação normal de (I) a
expressão para a aceleração do corpo durante a descida fica
µ N − PP sen 45° = M a D
µ M g cos 45° − M g sen 45° = M a D
a D = µ g cos 45° − g sen 45 °
(VI)
Da Cinemática Escalar temos que as equações de movimento do bloco durante a
subida e descida são
S = S 0 + v 0S . t S +
S − S 0 = v 0S . t S +
aS
t 2S
2
aS
t 2S
2
e
S = S 0 − v 0D . t D −
aD
S − S 0 = −v 0D . t D −
Os
intervalos
percorridos
na
subida
2
aD
2
t D2
t D2
e
descida
do
bloco
são
iguais
S − S 0 = AB = BA = ∆ S , então temos
∆ S = v 0S t S +
∆S = −
igualando as equações (VII) e (VIII)
3
aD
2
aS
2
t D2
t S2
(VII)
(VIII)
www.fisicaexe.com.br
aS
v 0S t S +
t S2 = −
2
aD
t D2
2
(IX)
Escrevendo a função da velocidade para o bloco subindo, temos
v S = v 0S + a S t S
0 = v 0S + a S t S
v 0S = −a S t S
(X)
substituindo (X) em (IX), obtemos
− a S .t S .t S +
− a S . t 2S +
aS
2
aS
2
t 2S = −
t 2S = −
− 2 a S . t 2S + a S . t S
−
2
aS
2
t 2S = −
2
=−
2
2
aD
2
aD
aD
t D2
t 2D
aD
2
t D2
t 2D
simplificando o fator 2 e o sinal negativo, reescrevemos
a S . t S2 = a D . t D2
t S2
t D2
=
aD
aS
2
tS 
a
  = D
 tD 
aS
 
Substituindo as acelerações na subida e na descida pelas expressões encontradas em
(IV) e (VI) respectivamente, temos
2
tS 
  = µ . g . cos 45° − g . sen 45°
 tD 
− µ . g . cos 45° − g . sen 45°
 
colocando a aceleração da gravidade g em evidência e substituindo cos 45° =
sen 45° =
2
2

2
2 
−
g . µ.

2
2 
tS 

  =
 tD 

2
2 
 
−
g . − µ.

2
2 

2
2
2
2
µ.
−
tS 
2
2
  =
 tD 
2
2
 
− µ.
−
2
2
4
2
2
e
www.fisicaexe.com.br
tS

 tD

2
.( µ − 1 )
2
2
.( − µ − 1)
2
2

 =


2
tS 
  = µ −1
 tD 
− µ −1
 
substituindo o coeficiente de atrito µ pelo valor dado fica
2
tS 
  = 2 − 3 −1
 tD 
− 2 − 3 −1
 
(
)
2
tS 
  = 1− 3
 tD 
− 2 + 3 −1
 
2
tS 
  = 1− 3
 tD 
−3+ 3
 
para racionalizar a expressão acima multiplicamos o numerador e o denominador por
−3−
3 , então
tS

 tD

(
(
2

 = 1− 3 . − 3 −

−3+ 3 −3−

2
tS 
  = −3−
tD 
 
tS

 tD

3 +3 3 +3
9−3
2

 =2 3

6

2
tS 
  = 3
 tD 
3
 
e finalmente
tS
tD
3
3
=
5
)
3)
3