calcule+ - WebLiessin

LISTA DE MATEMÁTICA I – nº 4 - 2º PERÍODO
Aluno (a):
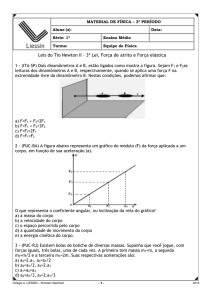
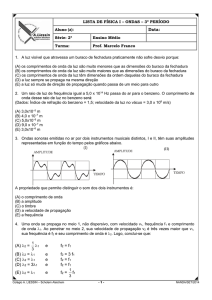
Data:
Nº:
Unidade: Botafogo
Ano: 9º
Profa: Nara Barat
3
1) Determine o valor da expressão √2√128 +
2) Calcule o valor da soma de √
3
3) O valor da expressão
164
1
83
∶
5
com √
2
2
5
.
2
√2
𝑹:
−
√2+1
√2−1
𝟕√𝟏𝟎
𝟏𝟎
4
2
2 é:
8
R: letra D
(a) 2−1
(b) 20
1
(c) 22
(d) 24
4) Simplifique a expressão
3√3 .√3 .√3
4
√27
.
Colégio Israelita Brasileiro A. Liessin Scholem Aleichem
𝟒
R: 𝟑√𝟐𝟕
1
+ 160,75 .
Nota:
R: √𝟐 + 𝟓
5) Resolva as equações, em IR:
a) (x + 2)2 = 2(x + 3)
b)
x2
3
−
x−9
6
=
𝑹: 𝑺 = {−√𝟐 , √𝟐}
3
𝟏
𝑹: 𝑺 = {𝟎 , 𝟐}
2
𝟏
c) (3y + 2)(y − 1) = y(y + 2)
d)
x2
x2 −4
−
x+1
3x−6
=
x
x+2
𝑹: 𝑺 = {− 𝟐 , 𝟐}
sendo U = IR – {-2 , 2}
mmc = 3(x-2)(x+2)
𝑹: x1 = 1 e x2 = 2
 2 não serve  𝑺 = {𝟏}
Colégio Israelita Brasileiro A. Liessin Scholem Aleichem
2
6) Sendo m e n as raízes da equação x(x − 2) = x + 4 , o valor de (2𝑚 )𝑛 é _ _ _ _ _ .
𝑹:
𝟏
𝟏𝟔
7) Qual o maior valor de m na equação 4𝑥 2 + 3𝑥 + 𝑚 + 2 = 0, que torna as raízes reais? Obs: ∆≥ 0
𝟐𝟑
𝑹: 𝒎 ≤ − 𝟏𝟔
8) Determine o valor de p na equação (𝑝2 − 1)𝑥 2 + (𝑝 + 1)𝑥 − (3𝑝 − 1) = 0 de modo que a soma do
1
inversos de suas raízes seja igual a .
𝑹: 𝒑 = 𝟑
2
9) Monte uma equação do 2o grau de coeficientes inteiros que tenha com raízes:
a) −1 e −
2
3
𝑹: 𝟑𝒙𝟐 + 𝟓𝒙 + 𝟐 = 𝟎
Colégio Israelita Brasileiro A. Liessin Scholem Aleichem
3
b)
1
4
e
3
𝑹: 𝟏𝟓𝒙𝟐 − 𝟏𝟔𝒙 + 𝟑 = 𝟎
4
10) Calcule o menor valor de m na equação 𝑚𝑥 2 − (3𝑚 − 1)𝑥 + 𝑚 = 0 , de modo que a razão entre
suas raízes seja
1
4
.
𝟐
𝑹: 𝒎 = 𝟏𝟏
11) Determine o valor de K na equação 𝑥 2 − 15𝑥 + 6𝑘 + 36 = 0 , de modo que a diferença entre
as raízes seja igual a 3. 𝑹: 𝑲 = 𝟑
Colégio Israelita Brasileiro A. Liessin Scholem Aleichem
4
12) Resolva a equação literal na incógnita x.
3𝑚𝑥 2 − (𝑚2 + 6)𝑥 + 2𝑚 = 0
𝒎
𝟐
𝑹: 𝑺 = { 𝟑 , 𝒎}
x
x
13) Sendo 𝑥1 e 𝑥2 as raízes da equação 𝑥 2 + 3𝑥 − 1 = 0, calcule x1 + x2 + 2.
2
1
𝑹: − 𝟗
14) Escreva as seguintes equações na forma fatorada.
a) 4𝑥 2 − 4𝑥 + 1 = 0
b) 8𝑥 2 − 6𝑥 + 1 = 0
𝑹: (𝟐𝒙 − 𝟏)𝟐
𝟏
𝟏
𝟐𝒙−𝟏
𝟒𝒙−𝟏
𝟐
𝟒
𝑹: 𝟖 (𝒙 − 𝟐) (𝒙 − 𝟒) = 𝟖 (
Colégio Israelita Brasileiro A. Liessin Scholem Aleichem
5
)(
) = (𝟐𝒙 − 𝟏)(𝟒𝒙 − 𝟏)
𝟓
𝟐𝒙+𝟓
c) 2𝑥 2 + 11𝑥 + 15 = 0
𝑹: 𝟐 (𝒙 + 𝟐) (𝒙 + 𝟑) = 𝟐 (
d) 6𝑥 2 − 𝑥 − 1 = 0
𝑹: 𝟔 (𝒙 − 𝟐) (𝒙 + 𝟑) = 𝟔 (
𝟏
𝟏
15) Simplifique:
a)
b)
c)
x2 − 2x
x2
+ 3x − 10
3x2 + x − 10
x2 − 4
5x2 − x − 4
x2
− 2x + 1
𝑹:
𝑹:
𝑹:
𝒙(𝒙 − 𝟐)
(𝒙 − 𝟐)(𝒙 + 𝟓)
𝟓
𝟑
𝟑(𝒙− )(𝒙 + 𝟐)
(𝒙 − 𝟐) (𝒙 +𝟐)
𝟒
𝟓
𝟓(𝒙+ )(𝒙−𝟏)
(𝒙−𝟏)𝟐
=
=
=
Colégio Israelita Brasileiro A. Liessin Scholem Aleichem
𝒙
𝒙+𝟓
𝟑𝒙−𝟓
𝒙−𝟐
𝟓𝒙+𝟒
𝒙−𝟏
6
𝟐
) (𝒙 + 𝟑) = (𝟐𝒙 + 𝟓)(𝒙 + 𝟑)
𝟐𝒙−𝟏
𝟑𝒙+𝟏
𝟐
𝟑
)(
) = (𝟐𝒙 − 𝟏)(𝟑𝒙 + 𝟏)