Lista de Exercícios 5 - Função Inversa - Gabarito

UNEMAT – Universidade do Estado de Mato Grosso
Campus Universitário de Sinop
Faculdade de Ciências Exatas e Tecnológicas
Curso de Engenharia Civil
Disciplina: Fundamentos de Matemática
Lista de Exercícios - Função Inversa
1) O gráfico de uma função f é o segmento de reta que une os pontos
( −3, 4) e (3, 0) . Se f −1 é a função inversa de f , determine f −1(2) .
y = ax + b
y = ax + b
4 = a( −3) + b
−3a + b = 4
0 = a(3) + b
3a + b = 0
−3a + b = 4

 3a + b = 0
2b = 4
b=2
y = ax + b ⇒ y = −
3a + b = 0
3a + 2 = 0
3a = −2
a = −2
3
2
x+2
3
2
x+2
3
2
x =− y +2
3
3 x = −2y + 6
y =−
2y = 6 − 3 x
6 − 3x
y=
2
6 − 3x
f −1 ( x ) =
2
6 − 3(2)
f −1(2) =
2
−1
f (2) = 0
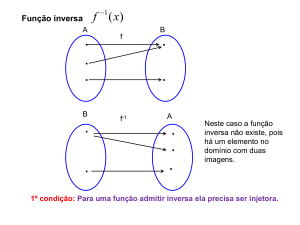
2) Seja a função f de ℝ − em ℝ + , definida por f ( x ) = x 2 . Qual é a função
inversa de f ?
A função dada é f ( x ) = y = x 2 com x ≤ 0 e y ≥ 0 .
Aplicando a regra prática, temos:
I) permutando as variáveis:
x = y 2 com y ≤ 0 e x ≥ 0
Página 1 de 6
UNEMAT – Universidade do Estado de Mato Grosso
Campus Universitário de Sinop
Faculdade de Ciências Exatas e Tecnológicas
Curso de Engenharia Civil
Disciplina: Fundamentos de Matemática
II) expressando y em função de x
x = y2
⇒
y= x
ou y = − x
Considerando que na função inversa f −1 devemos ter y ≤ 0 e
x ≥ 0 , a lei de correspondência da função inversa será f −1( x ) = − x .
Resposta: É a função f −1 de ℝ + em ℝ − definida por f −1( x ) = − x .
3) Seja a função bijetora f , de ℝ − {2} em ℝ − {1} definida por f ( x ) =
x +1
.
x −2
Qual é a função inversa de f ?
A função dada é f ( x ) = y =
x +1
com x ≠ 2 e y ≠ 1 .
x −2
Aplicando a regra prática, temos:
I) permutando as variáveis:
x=
y +1
com x ≠ 1 e y ≠ 2
y −2
II) expressando y em função de x
y +1
2x + 1
⇒ xy − 2 x = y + 1 ⇒ xy − y = 2 x + 1 ⇒ y ( x − 1) = 2 x + 1 ⇒ y =
y −2
x −1
2x + 1
f −1 ( x ) =
x −1
x=
f −1
Resposta: É a função
f −1( x ) =
de
ℝ − {1}
em
ℝ − {2}
definida por
2x + 1
.
x −1
4) Obtenha a função inversa da função f , de ℝ − {3} em ℝ − {−1} definida
por f ( x ) =
4−x
.
x −3
A função dada é f ( x ) = y =
4−x
com x ≠ 3 e y ≠ −1 .
x −3
Aplicando a regra prática, temos:
I) permutando as variáveis:
Página 2 de 6
UNEMAT – Universidade do Estado de Mato Grosso
Campus Universitário de Sinop
Faculdade de Ciências Exatas e Tecnológicas
Curso de Engenharia Civil
Disciplina: Fundamentos de Matemática
x=
4−y
com x ≠ −1 e y ≠ 3
y −3
II) expressando y em função de x
4−y
3x + 4
⇒ xy − 3 x = 4 − y ⇒ xy + y = 3 x + 4 ⇒ y ( x + 1) = 3 x + 4 ⇒ y =
y −3
x +1
3x + 4
f −1 ( x ) =
x +1
x=
Resposta: É a função f −1 de ℝ − {−1} em ℝ − {3} definida por
f −1( x ) =
3x + 4
.
x +1
5) Seja a função f de ℝ − {−2} em ℝ − {4} definida por f ( x ) =
4x − 3
. Qual
x+2
é o valor do domínio de f −1 com imagem 5 ?
Queremos determinar a ∈ ℝ − {4} tal que f −1(a ) = 5 ; para isso,
basta determinar a tal que f (5) = a .
a = f (5) =
4(5) − 3 17
=
5+2
7
⇒
a=
17
7
6) Seja a função f de A = {x ∈ ℝ / x ≤ −1} em B = {y ∈ ℝ / y ≥ 1} definida por
f ( x ) = x 2 + 2 x + 2 . Qual é o valor do domínio de f −1 com imagem −3 ?
Resolução 1:
A função dada é f ( x ) = y = x 2 + 2 x + 2 com x ≤ −1 e y ≥ 1 .
Aplicando a regra prática, temos:
I) permutando as variáveis:
x = y 2 + 2y + 2 com x ≥ 1 e y ≤ −1
II) expressando y em função de x
Página 3 de 6
UNEMAT – Universidade do Estado de Mato Grosso
Campus Universitário de Sinop
Faculdade de Ciências Exatas e Tecnológicas
Curso de Engenharia Civil
Disciplina: Fundamentos de Matemática
x = y 2 + 2y + 2 ⇒ ( x ) =
2
(
y 2 + 2y + 2
)
2
⇒ x 2 = y 2 + 2y + 2
y 2 + 2y + 1 + 1 = x 2 ⇒ ( y + 1)2 + 1 = x 2 ⇒ ( y + 1)2 = x 2 − 1
y + 1 = ± x 2 − 1 ⇒ y = −1 ± x 2 − 1
Como y ≤ −1 ⇒ y = −1 − x 2 − 1
Portanto f −1( x ) = −1 − x 2 − 1
−3 = −1 − x 2 − 1
x 2 − 1 = −1 + 3
(
x2 − 1 = 2
x2 − 1
)
2
= ( 2)
2
x2 − 1 = 4
x2 = 5
x=± 5
Como x ≥ 1 ⇒ x = 5
Resolução 2:
Queremos determinar a ∈ B = {x ∈ ℝ / x ≥ 1} tal que f −1(a ) = −3 ; para
isso, basta determinar a tal que f ( −3) = a .
a = f ( −3) = ( −3)2 + 2 ⋅ ( −3) + 2
⇒
a=± 5
Como x ≥ 1 ⇒ a = 5
7) Sejam os conjuntos A = {x ∈ ℝ / x ≥ 1} e B = {y ∈ ℝ / y ≥ 2} e a função f de
A em B definida por f ( x ) = x 2 − 2 x + 3 . Obtenha a função inversa de f .
A função dada é f ( x ) = y = x 2 − 2 x + 3 com x ≥ 1 e y ≥ 2 .
Aplicando a regra prática, temos:
I) permutando as variáveis:
x = y 2 − 2y + 3 com x ≥ 2 e y ≥ 1
II) expressando y em função de x
Página 4 de 6
UNEMAT – Universidade do Estado de Mato Grosso
Campus Universitário de Sinop
Faculdade de Ciências Exatas e Tecnológicas
Curso de Engenharia Civil
Disciplina: Fundamentos de Matemática
x = y 2 − 2y + 3 ⇒ x = y 2 − 2 y + 1 + 3 − 1 ⇒ x = ( y − 1) + 2 ⇒
2
⇒ ( y − 1) = x − 2 ⇒ y − 1 = ± x − 2 ⇒ y = 1 ± x − 2
2
Considerando que na função inversa f −1 devemos ter x ≥ 2 e
y ≥ 1 , a sentença que define a função inversa é f −1( x ) = 1 + x − 2 .
8) Seja a função f em ℝ definida por f ( x ) = 2 x + x + 1 − 2 x − 4 . Determine
a função inversa de f . Calcule f −1(42) .
 x + 1, se
x +1 = 
 − x − 1, se
x + 1 ≥ 0 ⇒ x ≥ −1
x + 1 < 0 ⇒ x < −1
 2x − 4, se
2x − 4 = 
−2 x + 4, se
2x − 4 ≥ 0 ⇒ x ≥ 2
2x − 4 < 0 ⇒ x < 2
-1
2
x +1 =
−x − 1
x +1
x +1
2x − 4 =
−2 x + 4
−2 x + 4
2x − 4
x −5
3x − 3
−x + 5
x + 1 − 2x − 4 =
2 x + x − 5,

f ( x ) = 2 x + 3 x − 3,
2 x − x + 5,

3 x − 5,

f ( x ) = 5 x − 3,
 x + 5,

se
x < −1
se
se
−1≤ x < 2
x≥2
se
x < −1
se
se
−1≤ x < 2
x≥2
y = 3x − 5
y = 5x − 3
x = 3y − 5
3y = x + 5
x = 5y − 3
5y = x + 3
x +5
3
x +5
f −1( x ) =
3
x +3
5
x +3
f −1( x ) =
5
y=
y=
Página 5 de 6
y = x +5
x = y +5
y = x −5
f −1( x ) = x − 5
UNEMAT – Universidade do Estado de Mato Grosso
Campus Universitário de Sinop
Faculdade de Ciências Exatas e Tecnológicas
Curso de Engenharia Civil
Disciplina: Fundamentos de Matemática
x + 5
 3 ,

x + 3
−1
f (x) = 
,
 5
 x − 5,


se
y < −1
se
− 1≤ y < 2
se
x+5
< −1 ⇒ x + 5 < −3
3
−1 ≤
y ≥2
⇒
x < −8
x +3
< 2 ⇒ −5 ≤ x + 3 < 10
5
x −5≥2
⇒
−8≤ x <7
x ≥7
⇒
x + 5
 3 ,

x + 3
−1
,
f (x) = 
 5
 x − 5,


se
x < −8
se
−8≤ x <7
se
x ≥7
Para x = 42 ⇒ f −1( x ) = x − 5 ⇒ f −1(42) = 42 − 5 ⇒ f −1(42) = 37
9) Dadas as funções f e g em ℝ , definidas por f ( x ) = 3 x − 2 e
g ( x ) = 2 x + 5 , determine a função inversa de g o f .
Determinamos inicialmente g o f e em seguida ( g o f ) :
−1
( g o f ) ( x ) = g (f ( x )) = 2f ( x ) + 5 = 2(3 x − 2) + 5 = 6 x + 1
Aplicando a regra prática, temos: x = 6 y + 1 ⇒ y =
(g o f )
−1
(x) =
x −1
6
Página 6 de 6
x −1
; portanto,
6